Spring Force Formula

Spring is a tool used daily by many of us and their inertia are frequently neglected by assuming it as massless. It’s an extremely casual activity that a Spring when strained, undergoes displacement when it is compacted it gets compressed and when it is free it comes to its equilibrium position. This fact tells us that spring exerts an equal as well as an opposite force on a body which compresses or stretches it.

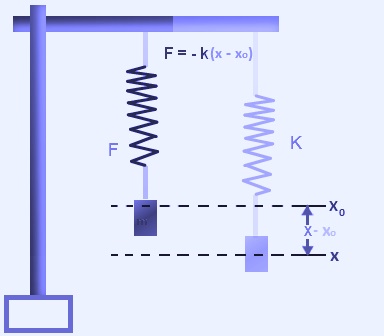
The Spring force formula is given by,

F = k(x – x₀)

Where,
the spring force is F,
the equilibrium position is x_o
the displacement of the spring from its position at equilibrium is x,
the spring constant is k.
The negative sign tells that the visualized spring force is a restoring force and acts in the opposite direction.

Spring Force Solved Problems

Problem 1: A spring has length 22 cm/s. If it is loaded with 2 kg, it gets stretched by 38 cm/s. Compute its spring constant.

Answer:

(Mass) m = 2 kg

(initial length) x_o = 22 cm

(displacement) x = 38 cm

Final displacement = x – x_o = 38 cm – 22 cm = 16 cm = 0.16 m

The spring force is articulated as,
F = ma
F = 2 kg × 0.16 m
F = 0.32 N

The spring constant is articulated as,

k = – 2 N/m

Thus, the spring constant is -2 N/m.

Problem 2: If a body is stretched by 2m with force 100 N. Calculate its spring constant.
Answer:
Known:

(Displacement) x = 2m

(force) F = 100 N

The spring constant is articulated as,

k = – 50 N/m

Thus, the spring constant is -50 N/m.