A cube is a three-dimensional solid figure. A cube is also known as the square solid that has edges with all the same length. In other words, the length, width, and height are equal, and each of its faces is a square. The main diagonal of a cube is the one that cuts through the centre of the cube; the diagonal of a face of a cube is not the main diagonal. The main diagonal of any cube can be found by multiplying the length of one side by the square root of 3.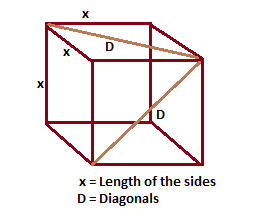

\[\LARGE Diagonal\;of\;a\;Cube=\sqrt{3}x\]