Cylindrical Capacitor
The capacitor is used to store large amounts of electric current in a small space. The cylindrical capacitor includes a hollow or a solid cylindrical conductor surrounded by the concentric hollow spherical cylinder. Capacitors are widely used in electric motors, flour mills, electric juicers and other electrical instruments. The potential difference between each capacitor varies. There are many electrical circuits where capacitors are to be grouped accordingly to get the desired capacitance. There are two common modes, including capacitors in series and capacitors in parallel. The unit of capacitance is Farad (F).
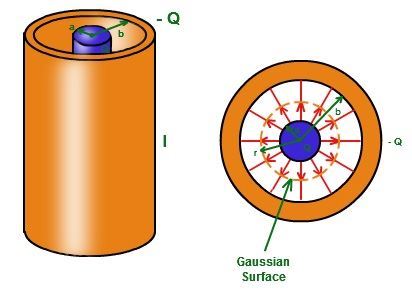
Cylindrical Capacitor
It is often used to store the electric charge. The Cylindrical capacitor is a type of capacitor that possesses a cylinder’s shape having an inner radius as a and outer radius as b.
The formula for the cylindrical capacitor is
Where,
C= capacitance of the cylinder
L = length of the cylinder
a = inner radius of the cylinder,
b = outer radius of the cylinder
Watch the video and learn to quantify the energy stored in a Cylindrical Capacitor

Solved Example
Example 1: A Cylindrical capacitor having a length of 8 cm is made of two concentric rings with an inner radius of 3 cm and an outer radius of 6 cm. Find the capacitance of the capacitor.
Answer:
Given:
Length L = 8 cm
inner radius a = 3 cm
outer radius b = 6 cm
The formula for the cylindrical capacitor is
Stay tuned with BYJU’S for more such interesting information.

Comments