Pythagorean Triples Formula

Pythagorean triples formula consist of three integers following the rules defined by the famous right-angled theorem or Pythagoras theorem. The proof for this theorem has already been given in our website.  The list of these triples are usually mentioned as Pythagorean triples and is commonly written in the form of (a, b, c). And the triangle formed with these triples is called a Pythagorean triangle. We will learn more here in this article with the help of examples.

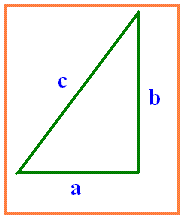
The Pythagorean Theorem Formula is expressed as,

c² = a² + b²

Formula for Pythagorean Triples

To find the Pythagorean triples, the following formula is used. If a, b are two sides of the triangle and c is the hypotenuse, then, a, b, and c can be found out using this-

• a = m²-n²
• b = 2mn
• c = m²+n²

These values result in a right-angled triangle with sides a, b, c.

Also, k.a, k.b and k.c are considered as the Pythagorean triple.

Notes:

(i) m, n and k are any two positive integers

(ii) m > n

(iii) m and n are coprime and both should not be odd numbers

Solves Example

Question: Check if (7, 24, 25) is a Pythagorean triple.

Solution: Given,

Pythagorean triple = (7, 24, 25)

a = 7, b = 24, c = 25

The Pythagorean triples formula is, c² = a² + b²

LHS: c² = 25² = 625

RHS: a² + b² = 7² + 24² = 49 + 576 = 625

LHS = RHS

So, (7, 24, 25) is a Pythagorean triple.

Pythagorean Triples List

Here is the list of the most commonly used Pythagorean triples: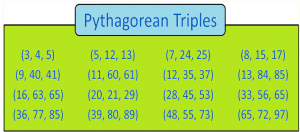

Learn more with us and download BYJU’S-The Learning App to get personalised videos.