Geometric mean formula, as the name suggests, is used to calculate the geometric mean of a set of numbers. To recall, the geometric mean (or GM) is a type of mean that indicates the central tendency of a set of numbers by using the product of their values. It is defined as the nth root of the product of n numbers. It should be noted that you cannot calculate the geometric mean from the arithmetic mean. In statistics, the geometric mean is well defined only for a positive set of real numbers. Example of using the formula for the geometric mean is to calculate the central frequency f0 of a bandwidth BW= f2–f1.
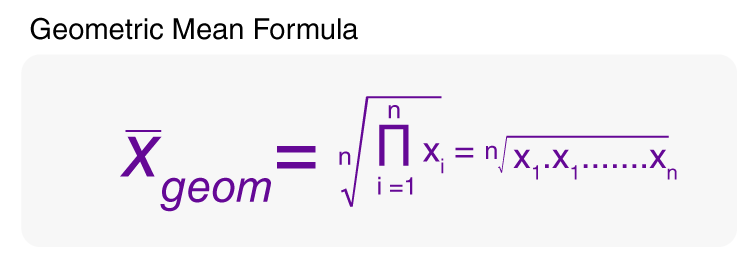
Formula to Calculate Geometric Mean
Formula for Geometric Mean
For GM formula, multiply all the “n” numbers together and take the “nth root of them. The formula for evaluating geometric mean is as follows if we have “n” number of observations.
| x̄geom = \(\begin{array}{l}\sqrt[n]{\prod_{i=1}^{n}x_{i}}=\sqrt[n]{x_{1}\cdot x_{2}\cdot\cdot\cdot x_{n}}\end{array} \) |
Notation in the GM Formula
- x̄geom is the geometric mean
- “n” is the total number of observations
- \(\begin{array}{l}\small \sqrt[n]{\prod_{i=1}^{n}x_{i}}\end{array} \)is the nth square root of the product of the given numbers.
Example Question Using Geometric Mean Formula
Question 1: Find the geometric mean of 4 and 3.
Solution: Using the formula for G.M., the geometric mean of 4 and 3 will be:
Geometric Mean will be √(4×3)
= 2√3
So, GM = 3.46
Question 2: What is the geometric mean of 4, 8, 3, 9 and 17?
Solution:
Step 1: n = 5 is the total number of values. Now, find 1/n.
1/5 = 0.2.
Step 2: Find geometric mean using the formula:
(4 × 8 × 3 × 9 × 17)0.2
So, geometric mean = 6.814
Articles Related to Geometric Mean
Keep visiting BYJU’S and get various other maths formulas which are explained in an easy way along with solved examples. Also, register now to get maths video lessons on different topics and several practice questions which will help to learn the maths concepts thoroughly.
Frequently Asked Questions
What is the Geometric Mean of 4 and 25?
Using the formula of geometric mean,
GM of 4, 25 = √(4×25) = √100
So, the geometric mean of 4 and 25 is 10.
How to Define Geometric Mean Formula?
Geometric mean formula is obtained by multiplying all the numbers together and taking the nth root of the product. Visit BYJU’S to learn more about the formula of geometric mean along with solved example questions.
Why Geometric Mean is Better than Arithmetic Mean?
Both the geometric mean and arithmetic mean are used to determine the average. For any two positive unequal numbers, the geometric mean is always less than the arithmetic mean. Now, the geometric mean is better since it takes indicates the central tendency. In certain cases, arithmetic mean works better like in representing average temperatures, etc.
Comments