Right Triangle Altitude Theorem:
This theorem describes the relationship between altitude drawn on the hypotenuse from vertex of the right angle and the segments into which hypotenuse is divided by altitude.
Consider a right angled triangle, \(\begin{array}{l}∆ABC\end{array} \)
which is right angled at \(\begin{array}{l}C\end{array} \)
.
If two triangles are similar to each other then,
i) Corresponding angles of both the triangles are equal and
ii) Corresponding sides of both the triangles are in proportion to each other.
Thus, two triangles \(\begin{array}{l}ΔABC\end{array} \)
and \(\begin{array}{l}ΔPQR\end{array} \)
are similar if
i) \(\begin{array}{l}∠A\end{array} \)
= \(\begin{array}{l}∠P\end{array} \)
, \(\begin{array}{l}∠B\end{array} \)
= \(\begin{array}{l}∠Q\end{array} \)
and \(\begin{array}{l}∠C\end{array} \)
= \(\begin{array}{l}∠R\end{array} \)
ii) \(\begin{array}{l}\frac{AB}{PQ}\end{array} \)
= \(\begin{array}{l}\frac{BC}{QR}\end{array} \)
= \(\begin{array}{l}\frac{AC}{PR}\end{array} \)
Using constructions in \(\begin{array}{l}ΔABC\end{array} \)
, let \(\begin{array}{l}∠DCA\end{array} \)
= \(\begin{array}{l}β\end{array} \)
and \(\begin{array}{l}∠DCB\end{array} \)
= \(\begin{array}{l}α\end{array} \)
as shown in fig. 2 below:
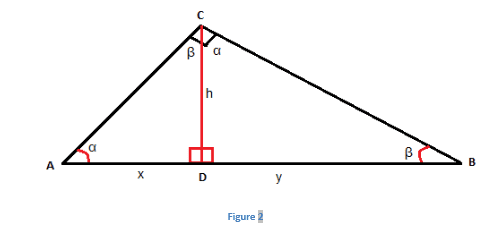
From fig. 2, in \(\begin{array}{l}ΔADC\end{array} \)
and \(\begin{array}{l}ΔBDC\end{array} \)
\(\begin{array}{l}∠ADC\end{array} \)
= \(\begin{array}{l}∠BDC\end{array} \)
(Both measure \(\begin{array}{l}90°\end{array} \)
)
As \(\begin{array}{l}ΔABC\end{array} \)
is right angled at \(\begin{array}{l}C\end{array} \)
:
\(\begin{array}{l}∠C\end{array} \)
= \(\begin{array}{l}α + β\end{array} \)
= \(\begin{array}{l}90°\end{array} \)
—(1)
In \(\begin{array}{l}∆ADC\end{array} \)
,
\(\begin{array}{l}∠ADC + ∠DCA + ∠CAD\end{array} \)
= \(\begin{array}{l}180°\end{array} \)
(Angle Sum Property)
\(\begin{array}{l}\Rightarrow\end{array} \)
\(\begin{array}{l}∠CAD\end{array} \)
= \(\begin{array}{l}180° – (90° + β)\end{array} \)
= \(\begin{array}{l}90° – β\end{array} \)
= \(\begin{array}{l}α\end{array} \)
(From equation 1)
Similarly in \(\begin{array}{l}∆BDC\end{array} \)
,
\(\begin{array}{l}∠BDC + ∠DCB + ∠CBD\end{array} \)
= \(\begin{array}{l}180°\end{array} \)
(Angle Sum Property)
\(\begin{array}{l}\Rightarrow∠CBD\end{array} \)
= \(\begin{array}{l}180° – (90° + α)\end{array} \)
= \(\begin{array}{l}90° – α\end{array} \)
= \(\begin{array}{l}β\end{array} \)
(From equation 1)
Thus by AA axiom of similarity
\(\begin{array}{l}∆ADC~∆CDB\end{array} \)
Thus in \(\begin{array}{l}ΔADC\end{array} \)
and \(\begin{array}{l}ΔBDC\end{array} \)
\(\begin{array}{l}\frac{CD}{BD}\end{array} \)
= \(\begin{array}{l}\frac{AD}{CD}\end{array} \)
\(\begin{array}{l}\Rightarrow~\frac{h}{y}\end{array} \)
= \(\begin{array}{l}\frac{x}{h}\end{array} \)
\(\begin{array}{l}\Rightarrow~h^2\end{array} \)
= \(\begin{array}{l}xy\end{array} \)
\(\begin{array}{l}⇔h\end{array} \)
= \(\begin{array}{l}√xy\end{array} \)
Thus, in a right angle triangle the altitude on hypotenuse is equal to the geometric mean of line segments formed by altitude on hypotenuse.
The converse of above theorem is also true which states that any triangle is a right angled triangle, if altitude is equal to the geometric mean of line segments formed by the altitude.
The above theorem can be easily comprehended by visualizing it.
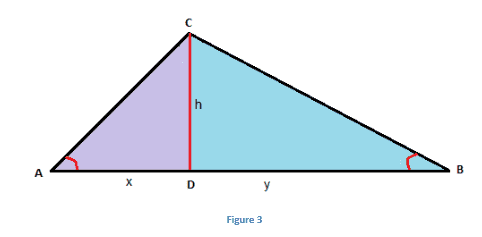
This figure can be represented by splitting \(\begin{array}{l}ΔADC \end{array} \)
and \(\begin{array}{l}ΔBDC\end{array} \)
along its altitude h and these dissected portions can be augmented and arranged into two different ways as shown below:
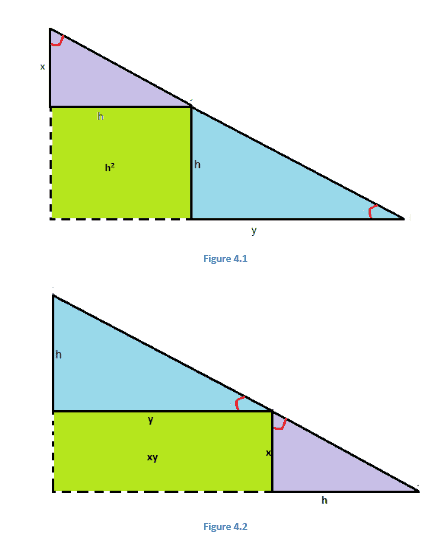
To complete the triangles in fig 4.1 and 4.2, a square of area \(\begin{array}{l}h^2\end{array} \)
units is added in fig 4.1 and a rectangle of area \(\begin{array}{l}xy\end{array} \)
units is appended to fig. 4.2. As, both figures represent the same triangle therefore the appended areas must be equal i.e., area of square and rectangle must be exactly the same.
\(\begin{array}{l}\Rightarrow~h^2\end{array} \)
= \(\begin{array}{l}xy\end{array} \)
\(\begin{array}{l}⇔h\end{array} \)
= \(\begin{array}{l}√xy\end{array} \)
<
‘






Comments