Sin2x Formula

The trigonometric formulas like Sin2x, Cos 2x, Tan 2x are known as double angle formulae. To understand this better, It is important to go through the practice examples provided.

Go through this article, and you will be able to:

• derive the double angle formulae using the addition formulae
• to write trigonometric expressions in different forms by using the formulae
• use the formulae for the solution of trigonometric equations

Introduction to Sin 2Theta formula

Here we look at trigonometric formulae known as the double angle formulae. They are called so because it involves double angles trigonometric functions, i.e. sin 2x.

Deriving Double Angle Formulae for Sin 2

\(\begin{array}{l}\Theta\end{array} \)

We start by recalling the addition formula to learn Sine double angle formula

sin(A + B) = sin A cos B + cos A sin B

Double Angle formula to get 2sinxcosx

Let’s see what happens if we let B equal to A.

After doing so, the first of these formulae becomes: sin(x + x) = sin x cos x + cos x sin x

so that sin2x = 2 sin x cos x.

And this is how our first double-angle formula, so called because we are doubling the angle (as in 2A).

Practice Example for Sin 2x

If we want to solve the following equation:

Sin 2x = sinx, -Π ≤ Π

We will follow the following steps:

Step 1) Use the Double angle formula

Sin 2x = 2 Sin x Cos x

Step 2) Let’s rearrange it and factorize

2Sinx Cosx – sinx = 0

Sin x(2 cos x -1) = 0

So, a) Sinx =0

or

b) cos2x -1 = 0

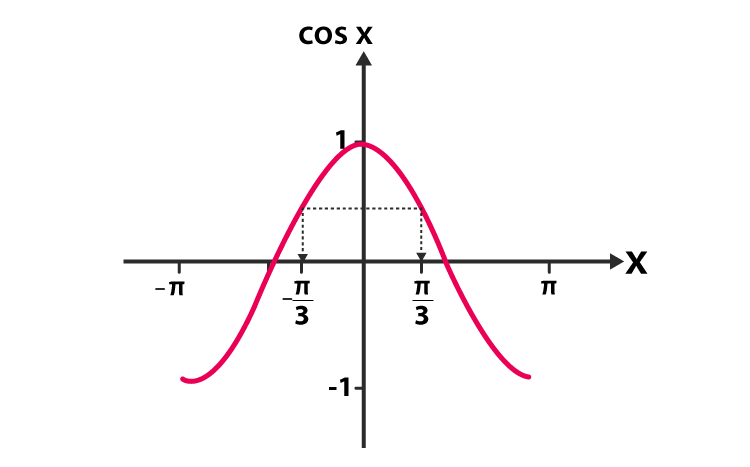
Step 3) Let’s consider Sin x = 0. (Refer to the graph)

We have two solutions as x = Π & x = 0.

Step 4) x = Π will be excluded as it isn’t in the interval mentioned in the question.

Step 5) from equation b, 2cosx -1 = 0

2 cos x = 1

Cos x =½

Cos x = 60⁰ or Π/3

Step 6) Looking at the graph, we infer that

x = – Π/3 & x = Π/3

To check other mathematical formulas and examples, visit BYJU’S.