Trajectory Formula
A trajectory is a path taken up by a moving object that is following through space as a function of time. Mathematically, a trajectory is described as a position of an object over a particular time. A much-simplified example would by a ball or rock was thrown upwards, the path taken by the stone is determined by the gravitational forces and resistance of air.
Some more common examples of trajectory motion would be a bullet fired from a gun, an athlete throwing a javelin, a satellite orbiting around the earth etc.
Trajectory formula is given by
\[\large y=x\:tan\,\theta-\frac{gx^{2}}{2v^{2}\,cos^{2}\,\theta}\]
Where,
y is the horizontal component,
x is the vertical component,
g= gravity value,
v= initial velocity,
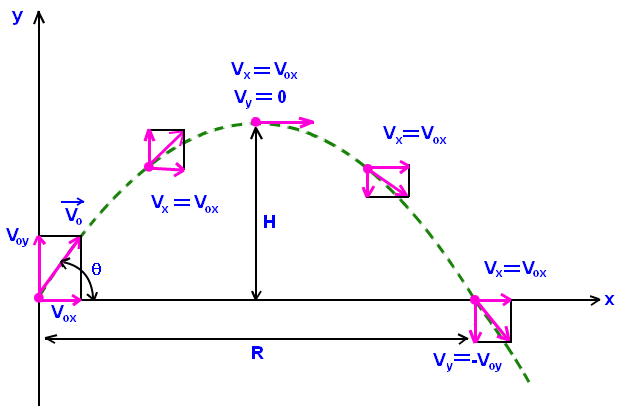
Trajectory related equations are:
\[\large Time\;of\;Flight: t=\frac{2v_{0}\,sin\,\theta}{g}\]
\[\large Maximum\;height\;reached: H=\frac{V_{0}^{2}\,sin^{2}\,\theta}{2g}\]
\[\large Horizontal\;Range: R=\frac{V_{0}^{2}\,sin\,2\,\theta}{g}\]
Where,
Vo is the initial Velocity,
sin
cos
Solved examples
Question: Marshall throws a ball at an angle of . If it moves at the rate of 6m/s and Steve catches it after 4s. Calculate the vertical distance covered by it.
Solution:
Given,
The horizontal distance is given by:
Comments