Unit Vector Formula
In mathematics, a unit vector in a normed vector space is a vector of length-1. A unit vector is often denoted by a lowercase letter with a “hat”
\(\begin{array}{l}\widehat{i}\end{array} \)
. The term direction vector is used to describe a unit vector being used to represent spatial direction, and such quantities are commonly denoted as d.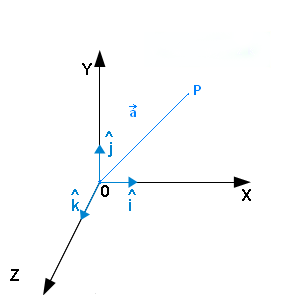
Two 2D direction vectors, d1 and d2, are illustrated. 2D spatial directions represented this way are equivalent numerically to points on the unit circle.
Unit Vector Formula is given by
\(\begin{array}{l}\hat{v}=\frac{\vec{v}}{|\vec{v}|}=\frac{(x \hat{i}, y \hat{j}, z \hat{k})}{\sqrt{x^{2}+y^{2}+z^{2}}}\end{array} \)
To check solved examples, click here.
Comments