A sphere is 3D or a solid shape having a completely round structure. If you rotate a circular disc along any of its diameters, the structure thus obtained can be seen as a sphere. You can also define it as a set of points which are located at a fixed distance from a fixed point in a three-dimensional space. This fixed point is known as the centre of the sphere. And the fixed distance is called its radius.
Formula to Calculate Volume of Sphere
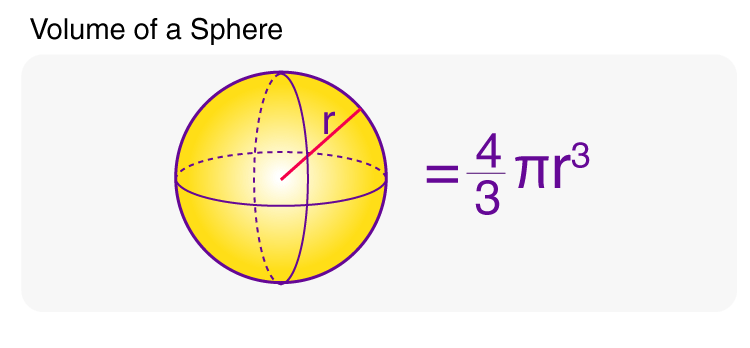
Volume of a Sphere Formula
In this section, you will learn the formula to compute the volume of a sphere. Volume, as you know, is defined as the capacity of a 3D object. The volume of a sphere is nothing but the space occupied by it. It can be given as:

\(\begin{array}{l}Volume \; of \; a \; sphere = \frac{4}{3}\pi r^{3}\end{array} \) |
Where ‘r’ represents the radius of the sphere.
Volume Of A Sphere Derivation
The volume of a sphere can alternatively be viewed as the number of cubic units which is required to fill up the sphere.
Consider a sphere of radius r and divide it into pyramids. In this way, we see that the volume of the sphere is the same as the volume of all the pyramids of height, r and total base area equal to the surface area of the sphere as shown in the figure.

The total volume is calculated by adding the pyramids’ volumes.
Volume of the sphere = Sum of volumes of all pyramids
Volume of the sphere=
Volume of the sphere =
Volume of a Sphere Formula in Real Life:
In our daily life, we come across different types of spheres. Basketball, football, table tennis, etc. are some of the common sports that are played by people all over the world. The balls used in these sports are nothing but spheres of different radii. The volume of sphere formula is useful in designing and calculating the capacity or volume of such spherical objects. You can easily find out the volume of a sphere if you know its radius.
Solved Examples Based on Sphere Volume Formula:
Question 1: A sphere has a radius of 11 feet. Find its volume.
Solution: Given,
r = 11 feet
We know that, volume of a sphere =
=
Question 2: The volume of a spherical ball is
Solution: Given,
Volume of the sphere=
We know that, volume of a sphere =
=
The radius of the ball is 4.34 cm (approx).
To solve more problems on the topic, download BYJU’S- The Learning App.

Comments