There are many types of triangles. Acute, Obtuse, Isosceles, Equilateral triangles. Out of these different triangles, few of them are special. When we say special, it means the sides and angles which are predictable and consistent.
Thirty sixty ninety triangle
Out of all the other shortcuts, 30-60-90 is indeed a special Triangle.
What is a 30-60-90 Triangle?
It is a triangle where the angles are always 30, 60 and 90. As one angle is 90, so this triangle is always a right triangle. Thus, these angles form a right-angled triangle. Also, the sum of two acute angles is equal to the right angle, and these angles will be in the ratio 1 : 2 or 2 : 1.
Sides of a 30 60 90 Triangle
As explained above, it is a unique triangle with particular values of lengths and angles. Thus, the sides of 30 60 and 90 triangles are considered to be the Pythagorean triples. In general, the sides of a triangle with angles 30 degrees, 60 degrees and 90 degrees can be expressed as given in the below table:
| The basic 30-60-90 triangle sides ratio is: | |
| The side opposite the 30° angle | x |
| The side opposite the 60° angle | x * √3 |
| The side opposite the 90° angle | 2x |
Facts about the sides of 30 60 90 triangle:
- The side opposite to the angle 30° is always the shortest since 30 degrees is the smallest angle
- The side opposite to the angle 60° will be the medium length since 60 degrees is the mid-sized degree angle in this triangle
- The side opposite to the angle 90° will always be the largest since 90 degrees is the largest. This side of the triangle is called the hypotenuse
Area of 30 60 90 Triangle Formula
Consider the triangle of 30 60 90 in which the sides can be expressed as:
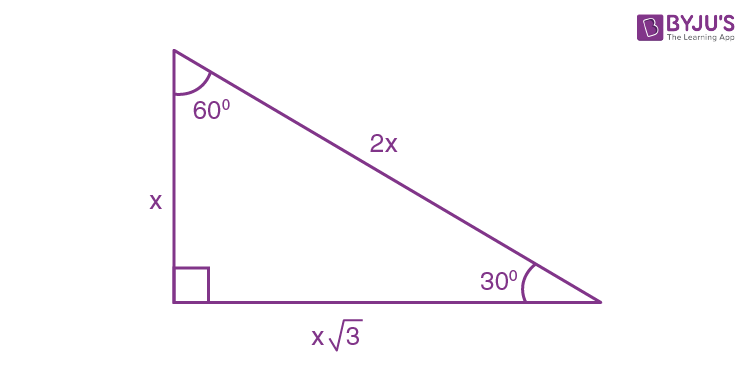
Here,
Base = x√3
Perpendicular (or Height) = x
Hypotenuse = 2x
We know that,
Area of triangle = (½) × Base × Height
= (½) × (x√3) × (x)
= (√3/2)x2
Example of 30 – 60 -90 rule
Example: Find the missing side of the given triangle.
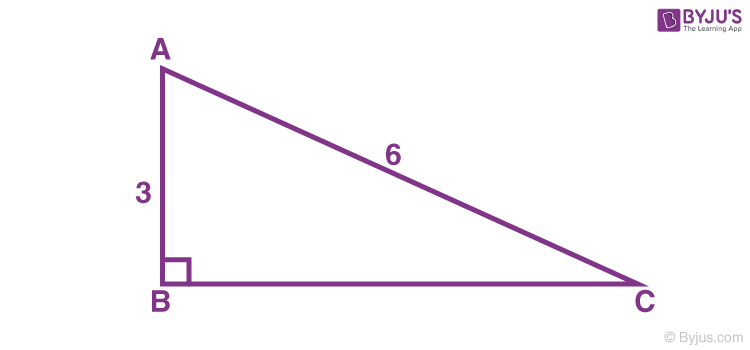
Solution:
As it is a right triangle in which the hypotenuse is the double of one of the sides of the triangle. Thus, it is called a 30-60-90 triangle where a smaller angle will be 30. The longer side is always opposite to 60° and the missing side measures 3√3 units in the given figure.
Visit BYJU’S to learn other important mathematical formulas.