Displacement Formula

Displacement is calculated as the shortest distance between starting and final point which prefers straight-line path over curved paths.

Suppose a body is moving in two different directions x and y then Resultant Displacement will be

It gives the shortcut paths for the given original paths.

Here,

u = Initial velocity

v = final velocity

a = acceleration

t = time taken.

Solved Examples

Problem 1: The path distance from the garden to a school is 5 m west and then 4 m south. A builder wants to build a short distance path for it. Find the displacement length of the shortest path.

Solution:

Given: Distance to the west x = 5 m

Distance to the south y = 4 m.

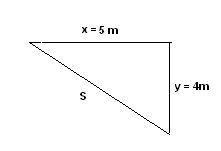
Displacement is given by

s = 6.403 m.

The builder can build a path for displacement length of 6.7 m.

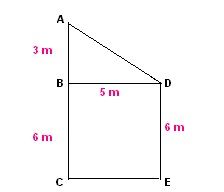
Question 2:A girl walks from the corridor to the gate she moves 3 m to the north opposite to her house then takes a left turn and walks for 5 m, then she takes right turn and moves for 6 m and reaches the gate. What is the displacement, magnitude, and distance covered by her?

Solution:

Total distance travelled d = 3 m + 5 m + 6 m = 14 m.

A magnitude of the displacement can be obtained by visualizing the walking. The actual path from A to B as 3 m then from B to D as 5 m and finally from D to E as 6 m.

So, the magnitude of the resultant displacement is

From figure AC = AB + BC = 3 m + 6 m = 9 m

BD = CE = 5 m

|S| =√92+52 = 10.29 m.

The direction of Resultant displacement is South East.