The Geometric series formula or the geometric sequence formula gives the sum of a finite geometric sequence. The geometric series is that series formed when each term is multiplied by the previous term present in the series. The sequence will be of the form {a, ar, ar2, ar3, …….}.
Geometric Series Formula
The geometric series formula is given by
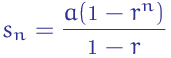
Here a will be the first term and r is the common ratio for all the terms, n is the number of terms.
Solved Example Questions Based on Geometric Series
Let us see some examples on geometric series.
Question 1: Find the sum of geometric series if a = 3, r = 0.5 and n = 5.
Solution:
Given:
a = 3
r = 0.5
n = 5
sn =
The sum of five terms is given by S5=
= 5.8125
Question 2: Find S10 if the series is 2, 40, 800,…..
Solution:
From the given,
a = 2
r = 20
n = 10
The 10th term in the series is given by S10 =
=
=

Comments