Pythagorean Theorem Formula

Pythagorean Theorem is one of the most fundamental theorems in mathematics and it defines the relationship between the three sides of a right-angled triangle. You are already aware of the definition and properties of a right-angled triangle. It is the triangle with one of its angles as a right angle, that is, 90 degrees. The side that is opposite to the 90-degree angle is known as the hypotenuse. The other two sides that are adjacent to the right angle are called legs of the triangle.

The Pythagoras theorem, also known as the Pythagorean theorem, states that the square of the length of the hypotenuse is equal to the sum of squares of the lengths of other two sides of the right-angled triangle. Or, the sum of the squares of the two legs of a right triangle is equal to the square of its hypotenuse.

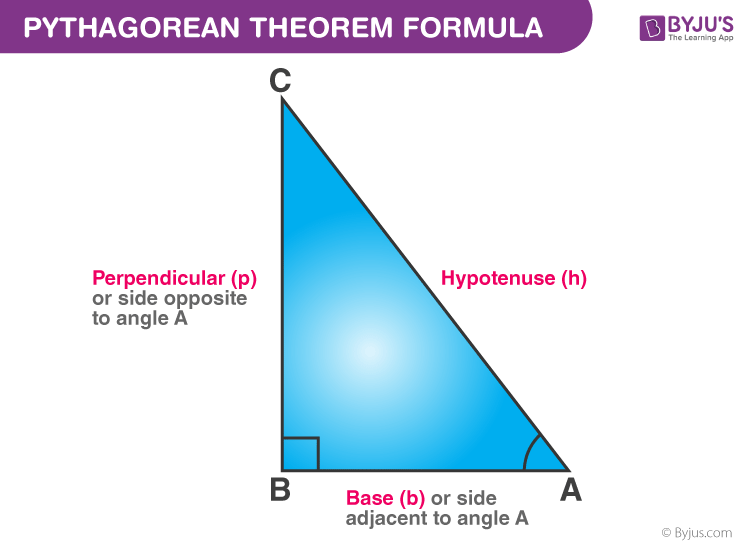Let us call one of the legs on which the triangle rests as its base. The side opposite to the right angle is its hypotenuse, as we already know. The remaining side is called the perpendicular. So, mathematically, we represent the Pythagoras theorem as:

Pythagorean Theorem Derivation

Consider a right-angled triangle ΔABC. From the below figure, it is right-angled at B.

Let BD be perpendicular to the side AC.

From the above-given figure, consider the  ΔABC and ΔADB,

In  ΔABC and ΔADB,

∠ABC = ∠ADB = 90°

  ∠A = ∠A → common

Using the AA criterion for the similarity of triangles, 

ΔABC ~ ΔADB 

Therefore, AD/AB = AB/AC

⇒ AB² = AC x AD  ……(1)

Considering  ΔABC and ΔBDC from the below figure.

∠C = ∠C  → common

 ∠CDB = ∠ABC = 90°

Using the Angle Angle(AA) criterion for the similarity of triangles, we conclude that,

ΔBDC ~ ΔABC

Therefore, CD/BC = BC/AC

⇒ BC² = AC x CD …..(2)

From the similarity of triangles, we conclude that,

∠ADB  = ∠CDB = 90°

So if a perpendicular is drawn from the right-angled vertex of a right triangle to the hypotenuse, then the triangles formed on both sides of the perpendicular are similar to each other and also to the whole triangle.

To Prove: AC² =AB² +BC²

By adding equation (1) and equation (2), we get:

AB² + BC²= (AC x AD) + (AC x CD)

AB² + BC² =  AC (AD + CD) …..(3)

Since AD + CD = AC, substitute this value in equation (3).

AB² + BC²=  AC (AC)

Now, it becomes

AB²+ BC²=  AC²

Hence, Pythagoras theorem is proved. 

Application of Pythagoras Theorem in Real Life

The following are the applications of the Pythagoras theorem:

• Pythagoras theorem is used to check if a given triangle is a right-angled triangle or not. 
• Aerospace scientists and meteorologists find the range and sound source using the Pythagoras theorem.
• It is used by oceanographers to determine the speed of sound in water.

Pythagorean Theorem Examples & Solutions

Question 1: Find the hypotenuse of a triangle whose lengths of two sides are 4 cm and 10 cm.

Solution: Using the Pythagoras theorem,

Hence, the hypotenuse of the triangle is 10.77 cm.

Question 2: If the hypotenuse of a right-angled triangle is 13 cm and one of the two sides is 5 cm, find the third side.

Solution: Given,

Hypotenuse a= 13 cm

One side b = 5 cm

Another side c = ?

Using the Pythagoras theorem,

Hence, the other side of the triangle is 12 cm.

To solve more problems on the topic, download BYJU’S – The Learning App.