The probability formula is used to compute the probability of an event to occur. To recall, the likelihood of an event happening is called probability. When a random experiment is entertained, one of the first questions that come in our mind is: What is the probability that a certain event occurs? A probability is a chance of prediction. When we assume that, let’s say, x be the chances of happening an event then at the same time (1-x) are the chances for “not happening” of an event.
Similarly, if the probability of an event occurring is “a” and an independent probability is “b”, then the probability of both the event occurring is “ab”. We can use the formula to find the chances of an event happening.
Formula to Calculate Probability
The formula of the probability of an event is:
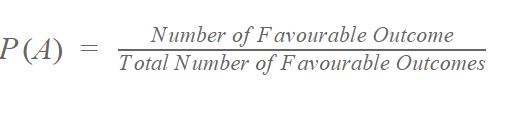
Probability Formula
Or,
| P(A) = n(A)/n(S) |
Where,
- P(A) is the probability of an event “A”
- n(A) is the number of favourable outcomes
- n(S) is the total number of events in the sample space
Note: Here, the favourable outcome means the outcome of interest.
Sometimes, students get confused about the word “favourable outcome” with “desirable outcome”. In some of the requirements, losing in a certain test or occurrence of an undesirable outcome can be a favourable event for the experiments run.
Basic Probability Formulas
Let A and B are two events. The probability formulas are listed below:
| All Probability Formulas List in Maths | |
|---|---|
| Probability Range | 0 ≤ P(A) ≤ 1 |
| Rule of Addition | P(A∪B) = P(A) + P(B) – P(A∩B) |
| Rule of Complementary Events | P(A’) + P(A) = 1 |
| Disjoint Events | P(A∩B) = 0 |
| Independent Events | P(A∩B) = P(A) ⋅ P(B) |
| Conditional Probability | P(A | B) = P(A∩B) / P(B) |
| Bayes Formula | P(A | B) = P(B | A) ⋅ P(A) / P(B) |
Example Questions Using Probability Formulas
Example 1: What is the probability that a card taken from a standard deck, is an Ace?
Solution:
Total number of cards a standard pack contains = 52
Number of Ace cards in a deck of cards = 4
So, the number of favourable outcomes = 4
Now, by looking at the formula,
Probability of selecting an ace from a deck is,
P(Ace) = (Number of favourable outcomes) / (Total number of favourable outcomes)
P(Ace) = 4/52
= 1/13
So we can say that the probability of getting an ace is 1/13.
Example 2: Calculate the probability of getting an odd number if a dice is rolled.
Solution:
Sample space (S) = {1, 2, 3, 4, 5, 6}
n(S) = 6
Let “E” be the event of getting an odd number, E = {1, 3, 5}
n(E) = 3
So, the Probability of getting an odd number is:
P(E) = (Number of outcomes favorable)/(Total number of outcomes)
= n(E)/n(S)
= 3/6
= ½
Probability is a very interesting topic, if learnt in the right way. You will be able to solve the probability problems on your own. Register with BYJU’S and find a new way to solve probability and other major maths topics now.
It was Good
Nice explain
Because of your learning process here I am confident of probability problems
thankyou BYJUS
i love this website i can get my questions answered y the livechat.
it was nice. THANK YOU BYJUS
I’m Francis P. Needu. I was glad to have come across your website in understanding math formulas and problems. I would really love to learn more math formulas and problems solving. Thanks eversomuch and I look forward to learning from you.
thanks a lot this helped me 😊🙏
Simple and easy explanation
Thanks for this opportunity to use this website it looks like hidden golden