The major difference between parabola and hyperbola is based on their eccentricity. For a parabola, eccentricity is equal to 1, and for hyperbola, eccentricity is greater than 1. Although both are part of conic sections, there are other differences too, which separate parabola and hyperbola from each other. See the graph below to understand the differences.
Definition of Parabola and Hyperbola
The section of the cone called a parabola is formed if a plane (flat surface) divides the conical surface, which presents parallel to the side of the cone.
Similarly, the conic section called hyperbola is formed when a plane divides the cone parallel to its axis.
Both the conic sections, parabola and hyperbola, are different in size, shape and other different criteria, including the formulas that are employed to determine them. In this article, let us understand how a parabola is different from a hyperbola.
What is the difference between Parabola and Hyperbola?
| Parabola | Hyperbola |
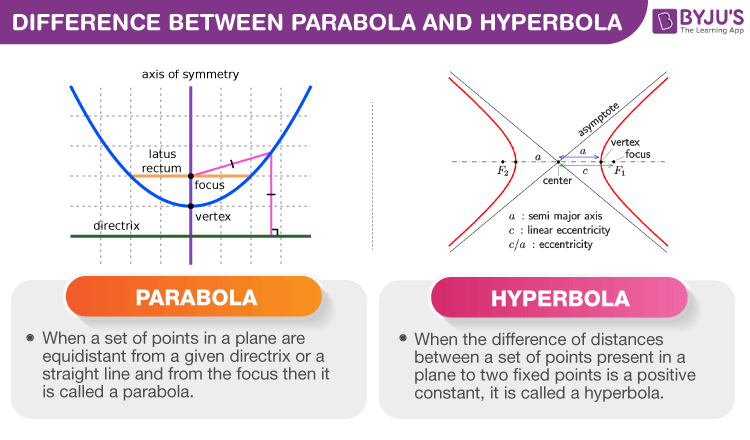
| A parabola is defined as a set of points in a plane which are equidistant from a straight line or directrix and focus. | The hyperbola can be defined as the difference of distances between a set of points, which are present in a plane to two fixed points, is a positive constant. |
| A parabola has single focus and directrix. | A hyperbola has two foci and two directrices. |
| Eccentricity, e = 1 | Eccentricity, e>1 |
| All parabolas should have the same shape irrespective of size. | The hyperbolas can be of different shapes. |
| The two arms present in a parabola should be parallel to each other. | The arms present in the hyperbola are not parallel to each other. |
| It has no asymptotes | It has two asymptotes |
Both hyperbolas and parabolas are open curves; in other words, the curve of the parabola and hyperbola does not end. It continues to infinity. But in the case of the circle and ellipse, the curves are closed curves.
Frequently Asked Questions – FAQs
What is a Parabola?
What is hyperbola?
What are the four conic sections?
Circle
Ellipse
Parabola
Hyperbola
What is the equation of parabola?
y2 = 4ax
What is the equation of hyperbola?
(x2/a2) – (y2/b2) = 1


Comments