Difference of Sets

We have learned how to perform addition, subtraction, multiplication, and division on numbers. We can apply each one of these operations on a pair of numbers to get another number. For example, when we subtract the pair of numbers 8 and 3, we get the number 5, i.e. the difference between 8 and 3 is 5. Likewise, there are certain operations that we can perform on two sets, which give rise to another set. In this article, you will learn one of the set operations, called the difference of sets, its definition, formulas and examples in detail.

Difference of Two Sets

The difference of the sets A and B in this order is the set of elements which belong to A but not to B. Symbolically, we write A – B and read as “ A minus B”.

The representation of A – B using a Venn diagram is given below.

Similarly, we can find B – A, the difference of the sets B and A in this order is the set of elements which belong to B but not to A. Symbolically, we write B – A and read as “ B minus A”. and a Venn diagram for B – A as:

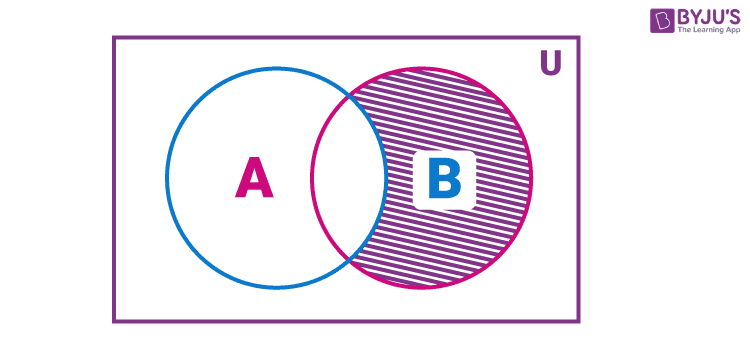
Also, note that A – B is not equal to B – A, i.e. A – B ≠ B – A.

Symmetric Difference between Two Sets

The set which contains the elements which are either in set A or in set B but not in both is called the symmetric difference between two given sets. It is represented by A ⊝ B and is read as a symmetric difference of set A and B.

Difference of Three Sets

It is possible to find the difference between three sets, say A, B and C.

Suppose A, B, and C are three non-empty sets, then A – B – C represents the set containing the elements of A that are not in B and C.

Venn diagram representation of A – B – C is given in the below diagram.

Some of the properties related to difference of sets are listed below:

• Suppose two sets A and B are equal then, A – B = A – A = ∅ (empty set) and B – A = B – B = ∅.
• The difference between a set and an empty set is the set itself, i.e, A – ∅ = A.
• The difference of a set from an empty set is an empty set, i.e, ∅ – A = ∅.
• The difference of a set, say A from universal set U is equal to empty set, i.e. A – U = ∅.
• When a superset is subtracted from a subset, then result is an empty set, i.e, A – B = ∅ if A ⊂ B
• If A and B are disjoint sets (no common elements for A and B), then A – B = A and B – A = B.

Let’s have a look at the solved examples given below to know how to calculate the difference of sets in case of two sets and three sets.

Difference of sets examples

Example 1:

If A = {1, 2, 3, 4, 5, 6} and B = {3, 4, 5, 6, 7, 8}, then find A – B and B – A.

Solution:

Given,

A = {1, 2, 3, 4, 5, 6}

B = {3, 4, 5, 6, 7, 8}

A – B = {1, 2} since the elements 1, 2 are there in A but not in B.

Similarly,

B – A = {7, 8}, since the elements 7 and 8 belong to B and not to A.

Also, we can show that A – B ≠ B – A.

Example 2:

If X = {11, 12, 13, 14, 15}, Y = {10, 12, 14, 16, 18} and Z = {7, 9, 11, 14, 18, 20}, then find the following:

(i) X – Y – Z

(ii) Y – X – Z

(iii) Z – X – Y

Solution:

Given,

X = {11, 12, 13, 14, 15}

Y = {10, 12, 14, 16, 18}

Z = {7, 9, 11, 14, 18, 20}

(i) X – Y – Z = {11, 12, 13, 14, 15} – {10, 12, 14, 16, 18} – {7, 9, 11, 14, 18, 20}

= {13, 15}

(ii) Y – X – Z = {10, 12, 14, 16, 18} – {11, 12, 13, 14, 15} – {7, 9, 11, 14, 18, 20}

= {10, 16}

(iii) Z – X – Y = {7, 9, 11, 14, 18, 20} – {11, 12, 13, 14, 15} – {10, 12, 14, 16, 18}

= {7, 9, 20}

Video Lesson on What are Sets

For more interesting maths concepts, download BYJU’S – The Learning App and learn all the maths and science concepts effectively and quickly.