The square root of 250 can be determined using different methods. We shall discuss a few methods that give a close approximation of the square root of 250 in this article. We get an irrational root because 250 is not a perfect square number. A perfect square number is a number that can be written as a square of an integer. The square root of a number is just the opposite of squaring. In radical form, the square root of 250 is denoted as √250, and in the exponential form, it is written as (250)½. Let us find the square root of 250.
Learn more about square and square roots.
|
Square Root of 250 |
|
|
Square of 250 |
62,500 |
What Is the Square Root of 250?
The square root of 250 is a number whose square gives the result 250. Now, 250 is not a perfect square number because we cannot find any integer that could be multiplied twice to get 250. Thus, we find an approximate value of the square root of 250, as it is an irrational number.
The square root of 250 can also be determined by finding the roots of the quadratic equation
x2 – 250 = 0
⇒ x2 = 250
Taking square roots on both sides, we get,
⇒ x = √250
⇒ x = ± 5√10
Let us verify, (5√10)2 = 5√10 × 5√10 = 5 × 5 × 10 = 25 × 10 = 250
How to Find the Square Root of 250?
Let us find the square root of 250 using the prime factorisation method, Newton’s formula, and the long division method. The repeated subtraction method will not work, as 250 is not a perfect square, and its square root is an irrational number.
Prime Factorisation Method
To find the square root of 250 by the prime factorisation method,
- First, prime factorise 250.
- Make pairs of two for each factor of 250.
- Take each pair once out of the square root.
- Finally, multiply each prime factor taken once out of the square root. If any factor cannot be paired in two, it could be simplified further.
The prime factorisation of 250 = 2 × 5 × 5 × 5
The square root of 250 = √[2 × 5 × 5 × 5] = 5 × √(2 × 5) = 5√10
Newton’s Formula
Newton’s formula to determine the approximate square root of any number (also referred to as the approximation method of finding the square root) is given by:
√N ≈ ½ (N/A + A), where
N is the number whose square root we need to find.
A is the approximate guess square root number.
Now, N = 250 and 152 = 225 < 250, we take A = 15
Let us substitute these values in the formula
√250 ≈ ½ (250/15 + 15) ≈ 15.8, which is a close approximation to the actual square root of 250.
Long Division Method
To find the square root of 250 by the long division method, we shall write 250 as the dividend and pair its digits from right to left. We shall calculate the square root as follows:
- While pairing from the right side, 2 remains unpaired. We put a pair of zeros after the number. Remember, whenever we go to the next step of division, both the paired numbers will come down together.
- Starting with 2, now 12 < 2 < 22; therefore, we subtract the square of 1 from 2, taking 1 as the quotient.
- For the next step, 1 + 1 = 2 becomes the first part of the divisor, and the remainder of 2 – 1 = 1, along with 50, that is 150, becomes the next dividend.
- 25 × 5 = 125 < 150, thus 25 times 5 goes into 150.
- For the next step, the first part of the divisor will be 25 + 5 = 30, and the dividend will be the remainder from 150 – 125 = 25, along with a pair of zeros, that is, 2500.
- Continuing this way, we get the square root of 250.
Note: The last divisor is always double the quotient. Using this fact, we can always verify our answer.
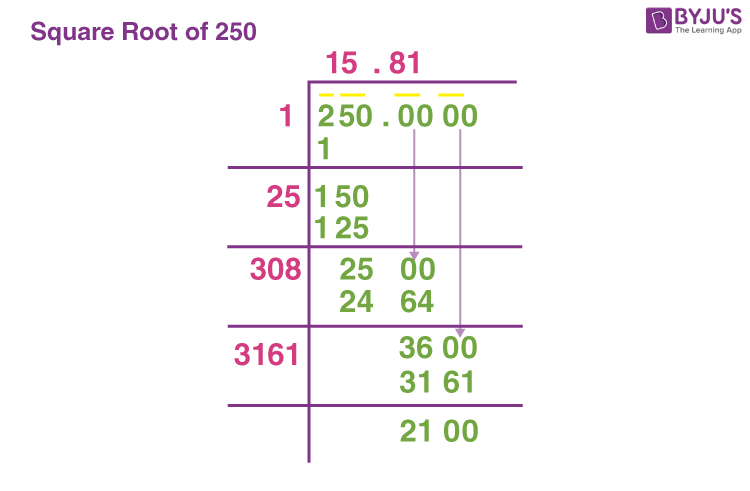
Thus, the square root of 250 = 15.81
To learn more about how to find the square root of any number by the long division method, click here.
Video Lessons on Square Root
Visualising square roots

Finding Square roots

Related Articles
Solved Examples on Square Root of 250
Example 1:
Find the radius of the sphere whose total surface area is 1000𝜋 cm2.
Solution:
Let r be the radius of the sphere.
The total surface area of the sphere = 4𝜋r2 = 1080𝜋 cm2
⇒ r2 = 1000/4 = 250 (taking square root on both the sides)
⇒ r = √250
⇒ r = 5√10 cm (taking the positive root as length cannot be negative)
∴ the radius of the sphere = 5√10 cm
Example 2:
Find the height of a parallelogram whose area is 125 cm2 and the base is half its height.
Solution:
Let h be the height of the parallelogram.
Base of the parallelogram = h/2
Area of the parallelogram = h × h/2 = 125 cm2
⇒ ½ × h2 = 125
⇒ h2 = 125 × 2 = 250 (taking square root on both the sides)
⇒ h = √250 = 5√10 ≈ 15.81 cm
∴ the height of the parallelogram is 15.81 cm.
Example 3:
What is the smallest number that should be subtracted from 250 to make it a perfect square number? Also, find the square root of that number obtained.
Solution:
Clearly, 225 = 152 < 250
Therefore, we must subtract 25 from 250 to make it a perfect square number.
250 – 25 = 225 and
√225 = ± 15
Frequently Asked Questions on Square Root of 250
What is the square root of 250?
The square root of 250 is 3√30 or 15.8113883 (approx.).
Is 250 a perfect square number?
No, as 250 is not a square of any integer.
Is the square root of 250 rational or irrational?
The square root of 250 is an irrational number.
What is the prime factorisation of 250?
The prime factorisation of 250 is 2 × 5 × 5 × 5.
Is the square root of 250 a real number?
Yes, the square root of 250 is a real number.
What is the cube root of 250?
The cube root of 250 is 6.2996052 (approx.).
What number should be divided from 250 to get a perfect square?
By the prime factorisation of 250 = 2 × 5 ×5 × 5, we see that 2 and 5 are left unpaired. Hence, we must divide 250 by 2 × 5 = 10. Therefore, 250 ÷ 10 = 25 is a perfect square number.