MSBSHSE Solutions For SSC (Class 10) Maths Part 1 Chapter 3 Arithmetic Progression

MSBSHSE Solutions For SSC (Class 10) Maths Part 1 Chapter 3 Arithmetic Progression, is provided here in PDF format, which can be downloaded for free. The Maharashtra Board Textbook Solutions for the chapter Arithmetic Progression have been designed accurately by Mathematics experts at BYJU’S. These serve as a reference tool for the students to do their homework and assignments, as well. These solutions for Class 10 contain the exercise-wise answers for all the chapters, thus being a very useful study material for the students studying in Class 10. Chapter 3 of Maharashtra Board Solutions for Class 10 Maths Arithmetic Progression explains sequence, arithmetic progression, and its applications. A set of numbers where the numbers are arranged in a definite order, like the natural numbers, is called a sequence. In Chapter 3, students will learn and solve exemplar problems based on sequences, terms in a sequence, arithmetic progression, nth term of an A.P, sum of first n terms of an A.P and application of A.P.

Download the PDF of Maharashtra Solutions For SSC Maths Part 1 Chapter 3 Arithmetic Progression

Access answers to Maths MSBSHSE Solutions For SSC Part 1 Chapter 3 – Arithmetic Progression

Practice set 3.1 Page no: 61

1. Which of the following sequences are A.P.? If they are A.P. find the common difference.

(1) 2, 4, 6, 8, . . .

Solution:

Given 2, 4, 6, 8, . . .

Here, the first term, a₁ = 2

Second term, a₂ = 4

And a₃ = 6

Now, common difference = a₂ – a₁ = 4 – 2 = 2

Also, a₃ – a₂ = 6 – 4 = 2

Since, the common difference is same.

Hence the terms are in Arithmetic progression with common difference, d = 2.

(2) 2, 5/2, 3, 7/3, . . .

Solution:

(3) – 10, – 6, – 2, 2, . . .

Solution:

Given – 10, – 6, – 2,2, . . .

Here, the first term, a₁ = – 10

Second term, a₂ = – 6

a₃ = – 2

Now, common difference = a₂ – a₁ = – 6 – (– 10) = – 6 + 10 = 4

Also, a₃ – a₂ = – 2 – (– 6) = – 2 + 6 = 4

Since, the common difference is same.

Hence the terms are in Arithmetic progression with common difference, d = 4.

(4) 0.3, 0.33, .0333, . . .

Solution:

Given 0.3, 0.33, 0.333, . . .

Here, the first term, a₁ = 0.3

Second term, a₂ = 0.33

a₃ = 0.333

Now, common difference = a₂ – a₁ = 0.33 – 0.3 = 0.03

Also, a₃ – a₂ = 0.333 – 0.33 = 0.003

Since, the common difference is not same.

Hence the terms are not in Arithmetic progression

(5) 0, – 4, – 8, – 12, . . .

Solution:

Given 0, – 4, – 8, – 12, . . .

Here, the first term, a₁ = 0

Second term, a₂ = – 4

a₃ = – 8

Now, common difference = a₂ – a₁ = – 4 – 0 = – 4

Also, a₃ – a₂ = – 8 – (– 4) = – 8 + 4 = – 4

Since, the common difference is same.

Hence the terms are in Arithmetic progression with common difference, d = – 4.

(6) -1/5, -1/5, – 1/5, . . .

Solution:

(7) 3, 3 + √2, 3 + 2√2, 3 + 3√2, ….

Solution:

Given

3, 3 + √2, 3 + 2√2, 3 + 3√2, ….

Here, the first term, a₁ = 3

Second term, a₂ = 3 + √2

a₃ = 3 + 2√2

Now, common difference = a₂ – a₁ = 3 + √2 – 3 = √2

Also, a₃ – a₂ = 3 + 2√2 – (3 + √2) = 3 + 2√2 – 3 – √2 = √2

Since, the common difference is same.

Hence the terms are in Arithmetic progression with common difference, d = √2.

(8) 127, 132, 137, . . .

Solution:

Given 127, 132, 137, . . .

Here, the first term, a₁ = 127

Second term, a₂ = 132

a₃ = 137

Now, common difference = a₂ – a₁ = 132 – 127 = 5

Also, a₃ – a₂ = 137 – 132 = 5

Since, the common difference is same.

Hence the terms are in Arithmetic progression with common difference, d = 5.

2. Write an A.P. whose first term is a and common difference is d in each of the following.

(1) a = 10, d = 5

Solution:

Given a = 10, d = 5

Let a₁ = a = 10

Since, the common difference d = 5

Using formula a_{n + 1} = a_n + d

Thus, a₂ = a₁ + d = 10 + 5 = 15

a_{3 =} a₂ + d = 15 + 5 = 20

a₄ = a₃ + d = 20 + 5 = 25

Hence, An A.P with common difference 5 is 10, 15, 20, 25, ….

(2) a = – 3, d = 0

Solution:

Given a = – 3, d = 0

Let a₁ = a = – 3

Since, the common difference d = 0

Using formula a_{n + 1} = a_n + d

Thus, a₂ = a₁ + d = – 3 + 0 = – 3

a_{3 =} a₂ + d = – 3 + 0 = – 3

a₄ = a₃ + d = – 3 + 0 = – 3

Hence, An A.P with common difference 0 is – 3, – 3, – 3, – 3, ….

(3) a = – 7, d = ½

Solution:

(4) a = – 1.25, d = 3

Solution:

Given a = – 1.25, d = 3

Let a₁ = a = – 1.25

Since, the common difference d = 3

Using formula a_{n + 1} = a_n + d

Thus, a₂ = a₁ + d = – 1.25 + 3 = 1.75

a_{3 =} a₂ + d = 1.75 + 3 = 4.75

a₄ = a₃ + d = 4.75 + 3 = 7.75

Hence, An A.P with common difference 3 is – 1.25, 1.75, 4.75, 7.75

(5) a = 6, d = – 3

Solution:

Given a = 6, d = – 3

Let a₁ = a = 6

Since, the common difference d = – 3

Using formula a_{n + 1} = a_n + d

Thus, a₂ = a₁ + d = 6 + (– 3) = 6 – 3 = 3

a_{3 =} a₂ + d = 3 + (– 3) = 3 – 3 = 0

a₄ = a₃ + d = 0 + (– 3) = – 3

Hence, An A.P with common difference – 3 is 6, 3, 0, – 3…

(6) a = – 19, d = – 4

Solution:

Given a = – 19, d = – 4

Let a₁ = a = – 19

Since, the common difference d = – 4

Using formula a_{n + 1} = a_n + d

Thus, a₂ = a₁ + d = – 19 + (– 4) = – 19 – 4 = – 23

a_{3 =} a₂ + d = – 23 + (– 4) = – 23 – 4 = – 27

a₄ = a₃ + d = – 27 + (– 4) = – 27 – 4 = – 31

Hence, An A.P with common difference – 4 is – 19, – 23, – 27, – 31, ….

3. Find the first term and common difference for each of the A.P.

(1) 5, 1, – 3, – 7, . . .

Solution:

Given 5, 1, – 3, – 7, . . .

First term a₁ = 5

Second term a₂ = 1

Third term a₃ = – 3

We know that d = a_{n + 1} – a_n

Thus, d = a₂ – a₁ = 1 – 5 = – 4

Hence, the common difference d = – 4 and first term is 5

(2) 0.6, 0.9, 1.2, 1.5, . . .

Solution:

Given 0.6, 0.9, 1.2, 1.5, . . .

First term a₁ = 0.6

Second term a₂ = 0.9

Third term a₃ = 1.2

We know that d = a_{n + 1} – a_n

Thus, d = a₂ – a₁ = 0.9 – 0.6 = 0.3

Hence, the common difference d = 0.3 and first term is 0.6

(3) 127, 135, 143, 151, . . .

Solution:

Given 127, 135, 143, 151, . . .

First term a₁ = 127

Second term a₂ = 135

Third term a₃ = 143

We know that d = a_{n + 1} – a_n

Thus, d = a₂ – a₁ = 135 – 127 = 8

Hence, the common difference d = 8 and first term is 127

(4) 1/4, ¾, 5/4, 7/4, . . .

Solution:

Practice set 3.2 Page no: 66

1. Write the correct number in the given boxes from the following A. P.

(1) 1, 8, 15, 22, . . .

Solution:

Given 1, 8, 15, 22, . . .

First term a = 1

Second term t₁ = 8

Third term t₂ = 15

Fourth term t₃ = 22

We know that d = t_{n + 1} – t_n

Thus, t₂ – t₁ = 15 – 8 = 7

t₃ – t₂ = 22 – 15 = 7

Thus, d = 7

(2) 3, 6, 9, 12, . . .

Solution:

Given 3,6,9,12, . . .

First term a = 3

Second term t₁ = 6

Third term t₂ = 9

Fourth term t₃ = 12

We know that d = t_{n + 1} – t_n

Thus, t₂ – t₁ = 9 – 6 = 3

t₃ – t₂ = 12 – 9 = 3

Thus, d = 3

(3) – 3, – 8, – 13, – 18, . . .

Solution:

Given – 3, – 8, – 13, – 18, . . .

First term a = – 3

Second term t₁ = – 8

Third term t₂ = – 13

Fourth term t₃ = – 18

We know that d = t_{n + 1} – t_n

Thus, t₂ – t₁ = – 13 – (– 8) = – 13 + 8 = – 5

t₃ – t₂ = – 18 – (– 13) = – 18 + 13 = – 5

Thus, d = – 5

(4) 70, 60, 50, 40, . . .

Solution:

Given 70, 60, 50, 40, . . .

First term a = 70

Second term t₁ = 60

Third term t₂ = 50

Fourth term t₃ = 40

We know that d = t_{n + 1} – t_n

Thus, t₂ – t₁ = 50 – 60 = – 10

t₃ – t₂ = 40 – 50 = – 10

Thus, d = – 10

2. – 12, – 5, 2, 9, 16, 23, 30, . . .

Solution:

Given A.P. is – 12, – 5, 2, 9, 16, 23, 30, . . .

Here first term a = – 12

Second term t₁ = – 5

Third term t₂ = 2

Common Difference d = t₂ – t₁ = 2 – (– 5) = 2 + 5 = 7

We know that, n^th term of an A.P. is

t_n = a + (n – 1) d

We need to find the 20^th term,

Here n = 20

Thus, t₂₀ = – 12 + (20 – 1) × 7

t₂₀ = – 12 + (19) × 7 = – 12 + 133 = 121

Thus, t₂₀ = 121

3. Given Arithmetic Progression 12, 16, 20, 24, . . . Find the 24th term of this progression.

Solution:

Given A.P. is 12, 16, 20, 24, . . .

Where first term a = 12

Second term t₁ = 16

Third term t₂ = 20

Common Difference d = t₂ – t₁ = 20 – 16 = 4

We know that, n^th term of an A.P. is t_n = a + (n – 1) d

We need to find the 24^th term,

Here n = 24

Thus, t₂₄ = 12 + (24 – 1) × 4

t₂₄ = 12 + (23) × 4 = 12 + 92 = 104

Thus, t₂₄ = 104

4. Find the 19th term of the following A.P.
7, 13, 19, 25, . . .

Solution:

Given A.P. is 7, 13, 19, 25, . . .

Where first term a = 7

Second term t₁ = 13

Third term t₂ = 19

Common Difference d = t₂ – t₁ = 19 – 13 = 6

We know that, n^th term of an A.P. is

t_n = a + (n – 1) d

We need to find the 19^th term,

Here n = 19

Thus, t₁₉ = 7 + (19 – 1) × 6

t₁₉ = 7 + (18) × 6 = 7 + 108 = 115

Thus, t₁₉ = 115

5. Find the 27th term of the following A.P.
9, 4, – 1, – 6, – 11, . . .

Solution:

Given A.P. is 9, 4, – 1, – 6, – 11, . . .

Where first term a = 9

Second term t₁ = 4

Third term t₂ = – 1

Common Difference d = t₂ – t₁ = – 1 – 4 = – 5

We know that, n^th term of an A.P. is t_n = a + (n – 1) d

We need to find the 27^th term,

Here n = 27

Thus, t₂₇ = 9 + (27 – 1) × (– 5)

t₂₇ = 9 + (26) × (– 5) = 9 – 130 = – 121

Thus, t₂₇ = – 121

6. Find how many three-digit natural numbers are divisible by 5.

Solution:

List of three-digit number divisible by 5 are

100, 105, 110, 115, ………. 995

Let us find how many such number are there?

From the above sequence, we know that

t_n = 995, a = 100

t₁ = 105, t₂ = 110

Thus, d = t₂ – t₁ = 110 – 105 = 5

Now, by using n^th term of an A.P. formula that is t_n = a + (n – 1) d

we can find value of “n”

Thus, on substituting all the value in formula we get,

995 = 100 + (n – 1) × 5

⇒ 995 – 100 = (n – 1) × 5

⇒ 895 = (n – 1) × 5

⇒ n – 1 = 895/5 = 179

⇒ n = 179 + 1 = 180

7. The 11^th term and the 21st term of an A.P. are 16 and 29 respectively, then find the 41^th term of that A.P.

Solution:

8. 11, 8, 5, 2, . . . In this A.P. which term is number – 151?

Solution:

By, given A.P. 11, 8, 5, 2, . . .

we have a = 11, t₁ = 8, t₂ = 5

Thus, d = t₂ – t₁ = 5 – 8 = – 3

Given t_n = – 151

Now, by using n^th term of an A.P. formula t_n = a + (n – 1) d

we can find value of “n”

Thus, on substituting all the value in formula we get,

– 151 = 11 + (n – 1) × (– 3)

⇒ – 151 – 11 = (n – 1) × (– 3)

⇒ – 162 = (n – 1) × (– 3)

⇒ n – 1 = -162/-3 = 54

⇒ n = 54 + 1 = 55

9. In the natural numbers from 10 to 250, how many are divisible by 4?

Solution:

The number divisible by 4 in between 10 to 250 are

12, 16, 20, 24, ………… 248

From the above sequence, we have

t_n = 248, a = 12

t₁ = 16, t₂ = 20

Thus, d = t₂ – t₁ = 20 – 16 = 4

Now, by using n^th term of an A.P. formula t_n = a + (n – 1) d

we can find value of “n”

Thus, on substituting all the value in formula we get,

248 = 12 + (n – 1) × 4

⇒ 248 – 12 = (n – 1) × 4

⇒ 236 = (n – 1) × 4

⇒ n – 1 = 236/3 = 59

⇒ n = 59 + 1 = 60

10. In an A.P. 17^th term is 7 more than its 10^th term. Find the common difference.

Solution:

Given t₁₇ = 7 + t₁₀ …… (1)

In t₁₇, n = 17

In t₁₀, n = 10

By using n^th term of an A.P. formula, t_n = a + (n – 1) d

where n = number of terms

a = first term

d = common difference

t_n = n^th term

Thus, on using formula in eq. (1) we get,

⇒ a + (17 – 1) d = 7 + (a + (10 – 1) d)

⇒ a + 16 d = 7 + (a + 9 d)

⇒ a + 16 d – a – 9 d = 7

⇒ 7 d = 7

⇒ d = 7/7 = 1

Thus, common difference “d” = 1

Practice set 3.3 Page no: 72

1. First term and common difference of an A.P. are 6 and 3 respectively; find S₂₇.

Solution:

2. Find the sum of first 123 even natural numbers.

Solution:

The first 123 even natural number is

2, 4, 6, …….

Where first term a = 2

Second term t₁ = 4

Third term t₂ = 6

Thus, common difference d = t₂ – t₁ = 6 – 4 = 2

n = 123

By using sum of n^th term of an A.P. is

3. Find the sum of all even numbers from 1 to 350.

Solution:

The even natural number between 1 to 350 is

2,4, 6, …….348

Where first term a = 2

Second term t₁ = 4

Third term t₂ = 6

Thus, common difference d = t₂ – t₁ = 6 – 4 = 2

t_n = 348 (As we have to find the sum of even numbers between 1 and 350 therefore excluding 350)

Now, by using n^th term of an A.P. formula t_n = a + (n – 1) d

where n = number of terms

a = first term

d = common difference

t_n = n^th terms

we can find value of “n” by substituting all the value in formula we get,

⇒ 348 = 2 + (n – 1) × 2

⇒ 348 – 2 = 2(n – 1)

⇒ 346 = 2(n – 1)

4. In an A.P. 19th term is 52 and 38th term is 128, find sum of first 56 terms.

Solution:

Given t₁₉ = 52 and t₃₈ = 128

Now we have to find the value of “a” and “d”

Using n^th term of an A.P. formula t_n = a + (n – 1) d

where n = no. of terms

a = first term

d = common difference

t_n = n^th terms

we will find value of “a” and “d”

Let, t₁₉ = a + (19 – 1) d

⇒ 52 = a + 18 d …. (1)

t₃₈ = a + (38 – 1) d

⇒ 128 = a + 37 d …. (2)

Subtracting equation (1) from equation (2), we get,

⇒ 128 – 52 = (a – a) + (37 d – 18 d)

⇒ 76 = 19 d

⇒ d = 76/19 = 4

Substitute value of “d” in equation (1) to get value of “a”

⇒ 52 = a + 18 ×4

⇒ 52 = a + 72

⇒ a = 52 – 72 = – 20

Now, to find value of S₅₆ we will using formula of sum of n terms

Where, n = no. of terms

a = first term

d = common difference

S_n = sum of n terms

Thus, substituting given value in formula we can find the value of S_n

⇒S₅₆ = 28 × [ – 40 + 55×4]

⇒S₅₆ = 28 × [ – 40 + 220]

⇒S₅₆ = 28 × 180 = 5040

Thus, S₅₆ = 5040

5. Complete the following activity to find the sum of natural numbers from 1 to 140 which are divisible by 4.

Solution:

The natural number divisible by 4 between 1 to 140 is

4, 8, 12, …….136

Where first term a = 4

Second term t₁ = 8

Third term t₂ = 12

Thus, common difference d = t₂ – t₁ = 12 – 8 = 4

t_n = 136

Now, by using n^th term of an A.P. formula

t_n = a + (n – 1) d

where n = no. of terms

a = first term

d = common difference

t_n = n^th terms

we can find value of “n” by substituting all the value in formula we get,

⇒ 136 = 4 + (n – 1) × 4

⇒ 136 – 4 = 4(n – 1)

⇒ 132 = 4(n – 1)

⇒ n – 1 = 132/4 = 33

⇒ n = 33 + 1 = 34

Now, by using sum of n^th term of an A.P. we will find its sum

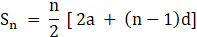
Where, n = no. of terms

a = first term

d = common difference

S_n = sum of n terms

Thus, substituting given value in formula we can find the value of S₃₄

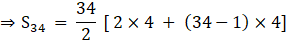
⇒S₃₄ = 17 × [8 + 33×4]

⇒S₃₄ = 17 × [8 + 132]

⇒S₃₄ = 17 × 140 = 2380

Thus, S₃₄ = 2380

6. Sum of first 55 terms in an A.P. is 3300, find its 28th term.

Solution:

⇒ a + 27d = 60 …… (1)

We need to find value of 28^th term that is t₂₈

Now, by using n^th term of an A.P. formula

t_n = a + (n – 1) d

where n = number of terms

a = first term

d = common difference

t_n = n^th terms

we can find value of t₂₈ by substituting all the value in formula we get,

⇒ t₂₈ = a + (28 – 1) d

⇒ t₂₈ = a + 27 d

From equation (1) we get,

⇒ t₂₈ = a + 27 d = 60

⇒ t₂₈ = 60

7. In an A.P. sum of three consecutive terms is 27 and their product is 504 find the terms? (Assume that three consecutive terms in A.P. are a – d, a, a + d.)

Solution:

Let the first term be a – d

the second term be a

the third term be a + d

Given sum of consecutive three term is 27

⇒ (a – d) + a + (a + d) = 27

⇒ 3 a = 27

⇒ a = 27/ 3 = 9

Also, given product of three consecutive term is 504

⇒ (a – d) × a × (a + d) = 504

⇒ (9 – d) × 9 × (9 + d) = 504 (since, a = 9)

⇒ (9 – d) × (9 + d) = 504/ 9 = 56

⇒ 9² – d² = 56 (since, (a – b) (a + b) = a² – b²)

⇒ 81 – d² = 56

⇒ d² = 81 – 56 = 25

⇒ d = √25 = ± 5

Case 1:

Thus, if a = 9 and d = 5

Then the three terms are,

First term a – d = 9 – 5 = 4

Second term a = 9

Third term a + d = 9 + 5 = 14

Thus, the A.P. is 4, 9, 14

Case 2:

Thus, if a = 9 and d = – 5

Then the three terms are,

First term a – d = 9 – (– 5) = 9 + 5 = 14

Second term a = 9

Third term a + d = 9 + (– 5) = 9 – 5 = 4

Thus, the A.P. is 14, 9, 4

8. Find four consecutive terms in an A.P. whose sum is 12 and sum of 3rd and 4th term is 14.
(Assume the four consecutive terms in A.P. are a – d, a, a + d, a + 2d.)

Solution:

Let the first term be a – d

the second term be a

the third term be a + d

the fourth term be a + 2 d

Given sum of consecutive four term is 12

⇒ (a – d) + a + (a + d) + (a + 2d) = 12

⇒ 4 a + 2d = 12

⇒ 2(2 a + d) = 12

⇒ 2a + d = 12/2 = 6

⇒ 2a + d = 6 …. (1)

Also, sum of third and fourth term is 14

⇒ (a + d) + (a + 2d) = 14

⇒ 2a + 3d = 14 …… (2)

Subtracting equation (1) from equation (2) we get,

⇒ (2a + 3d) – (2a + d) = 14 – 6

⇒ 2a + 3d – 2a – d = 8

⇒ 2d = 8

⇒ d = 8/2 = 4

⇒ d = 4

Substituting value of “d” in equation (1) we get,

⇒ 2a + 4 = 6

⇒ 2a = 6 – 4 = 2

⇒ a = 2/2 = 1

⇒ a = 1

Thus, a = 1 and d = 4

Hence, first term a – d = 1 – 4 = – 3

the second term a = 1

the third term a + d = 1 + 4 = 5

the fourth term a + 2 d = 1 + 2×4 = 1 + 8 = 9

Thus, the A.P. is – 3, 1, 5, 9

9. If the 9th term of an A.P. is zero then show that the 29^th term is twice the 19^th term.

Solution:

By using n^th term of an A.P. formula

t_n = a + (n – 1) d

where n = number of terms

a = first term

d = common difference

t_n = n^th terms

Given: t₉ = 0

⇒ t₉ = a + (9 – 1) d

⇒ 0 = a + 8d

⇒ a = – 8d

To Show: t₂₉ = 2× t₁₉

Now,

⇒ t₂₉ = a + (29 – 1) d

⇒ t₂₉ = a + 28d

⇒ t₂₉ = – 8d + 28d = 20 d (since, a = – 8d)

⇒ t₂₉ = 20 d

⇒ t₂₉ = 2 × 10 d …. (1)

Also,

⇒ t₁₉ = a + (19 – 1) d

⇒ t₁₉ = a + 18d

⇒ t₁₉ = – 8d + 18d = 10 d (since, a = – 8d)

⇒ t₁₉ = 10 d …. (2)

From equation (1) and equtaion (2) we get,

t₂₉ = 2 × t₁₉

Practice set 3.4 Page no: 78

1. On 1^st Jan 2016, Sanika decides to save ₹ 10, ₹ 11 on second day, ₹ 12 on third day. If she decides to save like this, then on 31st Dec 2016 what would be her total saving?

Solution:

According to the question we can form an A.P.

10, 11, 12, 13, ……

Hence, the first term a = 10

Second term t₁ = 11

Third term t₂ = 12

Thus, common difference d = t₂ – t₁ = 12 – 11 = 1

Here, number of terms from 1^st Jan 2016 to 31^st Dec 2016 is,

n = 366

We need to find S₃₆₆

Now, by using sum of n^th term of an A.P. we will find its sum

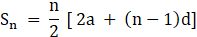
Where, n = no. of terms

a = first term

d = common difference

S_n = sum of n terms

Thus, on substituting the given value in formula we get,

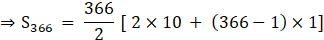
⇒S₃₆₆ = 183 [ 20 + 365]

⇒S₃₆₆ = 183 × 385

⇒S₃₆₆ = Rs 70,455

2. A man borrows ₹ 8000 and agrees to repay with a total interest of ₹ 1360 in 12 monthly instalments. Each instalment being less than the preceding one by ₹ 40. Find the amount of the first and last instalment.

Solution:

Given A man borrows = Rs. 8000

Repay with total interest = Rs 1360

In 12 months, thus n = 12

Thus, S₁₂ = 8000 + 1360 = 9360

Each installment being less than preceding one

Thus, d = – 40

We need to find “a”

Now, by using sum of n^th term of an A.P. we will find its sum

Thus, last installment t_n = 560

3. Sachin invested ina national saving certificate scheme. In the first year he invested ₹ 5000, in the second year ₹ 7000, in the third year ₹ 9000 and so on. Find the total amount that he invested in 12 years.

Solution:

According to the question we can form an A.P.

5000, 7000, 9000, ……

Hence, the first term a = 5000

Second term t₁ = 7000

Third term t₂ = 9000

Thus, common difference d = t₂ – t₁ = 9000 – 7000 = 2000

Here, number of terms n = 12

We need to find S₁₂

Now, by using sum of n^th term of an A.P. we will find its sum

Where, n = no. of terms

a = first term

d = common difference

S_n = sum of n terms

Thus, on substituting the given value in formula we get,

⇒S₁₂ = 6 × [ 10,000 + 11 × 2000]

⇒S₁₂ = 6 × [10,000 + 22,000]

⇒S₁₂ = 6 × 32,000

⇒S₁₂ = Rs. 192000

4. There is an auditorium with 27 rows of seats. There are 20 seats in the first row, 22 seats in the second row, 24 seats in the third row and so on. Find the number of seats in the 15th row and also find how many total seats are there in the auditorium?

Solution:

Given first term a = 20

Second term t₁ = 22

Third term t₂ = 24

Common difference d = t₂ – t₁ = 24 – 22 = 2

We need to find t₁₅ thus n = 15

Now, by using n^th term of an A.P. formula

t_n = a + (n – 1) d

where n = number of terms

a = first term

d = common difference

t_n = n^th terms

On substituting all value in n^th term of an A.P.

⇒ t₁₅ = 20 + (15 – 1) × 2

⇒ t₁₅ = 20 + 14 × 2

⇒ t₁₅ = 20 + 28 = 48

We have been given that, there are 27 rows in an auditorium

Thus, we need to find total seats in auditorium i.e. S₂₇

Now, by using sum of n^th term of an A.P. we will find its sum

Where, n = number of terms

a = first term

d = common difference

S_n = sum of n terms

Thus, on substituting the given value in formula we get,

⇒S₂₇ = 27 × 46

⇒S₂₇ = 1242

5. Kargil’s temperature was recorded in a week from Monday to Saturday. All readings were in A.P. The sum of temperatures of Monday and Saturday was 5° C more than sum of temperatures of Tuesday and Saturday. If temperature of Wednesday was – 30° Celsius then find the temperature on the other five days.

Solution:

Let Monday be the first term i.e. a = t₁

Let Tuesday be the second term that is t₂

Let Wednesday be the third term that is t₃

Let Thursday be the fourth term that is t₄

Let Friday be the fifth term that is t₅

Let Saturday be the sixth term that is t₆

Given: t₁ + t₆ = 5 + (t₂ + t₆)

⇒ a = 5 + (t₂ + t₆) – t₆

⇒ a = 5 + t₂ …. (1)

We know that,

Now, by using n^th term of an A.P. formula

t_n = a + (n – 1) d

where n = no. of terms

a = first term

d = common difference

t_n = n^th terms

Thus, t₂ = a + (2 – 1) d

⇒ t₂ = a + d

Now substitute value of t₂ in (1) we get,

⇒ a = 5 + (a + d)

⇒ d = a – 5 – a = – 5

Given: t₃ = – 30°

Thus, t₃ = a + (3 – 1) × (– 5)

⇒ – 30 = a + 2 × (– 5)

⇒ – 30 = a – 10

⇒ a = – 30 + 10 = – 20°

Thus, Monday, a = t₁ = – 20°

Using formula t_{n + 1} = t_n + d

We can find the value of the other terms

Tuesday, t₂ = t₁ + d = – 20 – 5 = – 25°

Wednesday, t₃ = t₂ + d = – 25 – 5 = – 30°

Thursday, t₄ = t₃ + d = – 30 – 5 = – 35°

Friday, t₅ = t₄ + d = – 35 – 5 = 40°

Saturday, t₆ = t₅ + d = – 40 – 5 = – 45°

Thus, we obtain an A.P.

– 20°, – 25°, – 30°, – 35°, – 40°, – 45°

6. On the world environment day tree plantation programme was arranged on a land which is triangular in shape. Trees are planted such that in the first row there is one tree, in the second row there are two trees, in the third row three trees and so on. Find the total number of trees in the 25 rows.

Solution:

First term a = 1

Second term t₁ = 2

Third term t₃ = 3

Common difference d = t₃ – t₂ = 3 – 2 = 1

We need to find total number of trees when n = 25

Thus, by using sum of n^th term of an A.P. we will find its sum

Where, n = no. of terms

a = first term

d = common difference

S_n = sum of n terms

We need to find S₂₅

Thus, on substituting the given value in formula we get,

Problem set 3 Page no: 78

1. Choose the correct alternative answer for each of the following sub questions.

(1) Choose the correct alternative answer for each of the following sub questions.
The sequence – 10, – 6, – 2, 2, . . .
A. is an A.P., Reason d = – 16
B. is an A.P., Reason d = 4
C. is an A.P., Reason d = – 4
D. is not an A.P.

Solution:

B. is an A.P., Reason d = 4

Explanation:

First term a = – 10

Second term t₁ = – 6

Third term t₂ = – 2

Fourth term t₃ = 2

Common difference d = t₁ – a = – 6 – (– 10) = – 6 + 10 = 4

Common difference d = t₂ – t₁ = – 2 – (– 6) = – 2 + 6 = 4

Common difference d = t₃ – t₂ = 2 – (– 2) = 2 + 2 = 4

Since, the common difference is same

∴ The given sequence is A.P. with common difference d = 4

Hence, correct answer is (B)

(2) First four terms of an A.P. are ….., whose first term is – 2 and common difference is – 2.
A. – 2, 0, 2, 4
B. – 2, 4, – 8, 16
C. – 2, – 4, – 6, – 8
D. – 2, – 4, – 8, – 16

Solution:

C. – 2, – 4, – 6, – 8

Explanation:

Given first term t₁ = – 2

Common difference d = – 2

By using formula t_{n + 1} = t_n + d

t₂ = t₁ + d = – 2 + (– 2) = – 2 – 2 = – 4

t₃ = t₂ + d = – 4 + (– 2) = – 4 – 2 = – 6

t₄ = t₃ + d = – 6 + (– 2) = – 6 – 2 = – 8

Hence, the A.P. is – 2, – 4, – 6, – 8

∴ correct answer is (C)

(3) What is the sum of the first 30 natural numbers?
A. 464
B. 465
C. 462
D. 461

Solution:

B. 465

Explanation:

List of first 30 natural number is

1, 2, 3, ……..,30

First term a = 1

Second term t₁ = 2

Third term t₂ = 3

Common difference d = t₃ – t₂ = 3 – 2 = 1

number of terms n = 30

Thus, by using sum of n^th term of an A.P. we will find its sum

Where, n = number of terms

a = first term

d = common difference

S_n = sum of n terms

We need to find S₃₀

⇒ S₃₀ = 15 [ 2 + 29]

⇒ S₃₀ = 15 × 31

⇒ S₃₀ = 465

Hence, Correct answer is (B)

(4) For a given A.P. t₇ = 4, d = – 4 then a = . . .
A. 6
B. 7
C. 20
D. 28

Solution:

D. 28

Explanation:

By using n^th term of an A.P. formula

t_n = a + (n – 1) d

where n = number of terms

a = first term

d = common difference

t_n = n^th terms

⇒ t₇ = a + (7 – 1) × (– 4)

⇒ 4 = a + 6 × (– 4)

⇒ 4 = a – 24

⇒ a = 24 + 4 = 28

Thus, the correct answer is (D)

(5) For a given A.P. a = 3.5, d = 0, n = 101, then t_n = . . .
A. 0
B. 3.5
C. 103.5
D. 104.5

Solution:

B. 3.5

Explanation:

Given: a = 3.5, d = 0, n = 101

By using n^th term of an A.P. formula

t_n = a + (n – 1) d

where n = number of terms

a = first term

d = common difference

t_n = n^th terms

Substituting all given value in the formulae we get,

⇒ t_n = 3.5 + (101 – 1) × 0

⇒ t_n = 3.5

Thus, correct answer is (B)

(6) In an A.P. first two terms are – 3, 4 then 21^st term is . . .
A. – 143
B. 143
C. 137
D. 17

Solution:

C. 137

Explanation:

Given first term a = – 3

Second term t₁ = 4

Common difference d = t₁ – a = 4 – (– 3) = 4 + 3 = 7

We need to find t₂₁ where n = 21

Now, by using n^th term of an A.P. formula

t_n = a + (n – 1) d

where n = no. of terms

a = first term

d = common difference

t_n = n^th terms

Substituting all given value in the formulae we get,

⇒ t₂₁ = – 3 + (21 – 1) × 7

⇒ t₂₁ = – 3 + 20 × 7

⇒ t₂₁ = – 3 + 140 = 137

Hence, correct answer is (C)

(7) If for any A.P. d = 5 then t₁₈ – t₁₃ = …
A. 5
B. 20
C. 25
D. 30

Solution:

C. 25

Explanation:

Given d = 5

By using n^th term of an A.P. formula

t_n = a + (n – 1) d

where n = number of terms

a = first term

d = common difference

t_n = n^th terms

Thus, t₁₈ – t₁₃ = [a + (18 – 1) × 5] – [ a + (13 – 1) × 5]

⇒ t₁₈ – t₁₃ = [ 17 × 5] – [ 12 × 5]

⇒ t₁₈ – t₁₃ = 85 – 60 = 25

Thus, correct answer is (C)

(8) Sum of first five multiples of 3 is. . .
A. 45
B. 55
C. 15
D. 75

Solution:

A. 45

Explanation:

First five multiples of 3 are

3, 6, 9, 12, 15

First term a = 3

Second term t₁ = 6

Third term t₂ = 9

Common difference d = t₂ – t₁ = 9 – 6 = 3

Thus, by using sum of n^th term of an A.P. we will find its sum

Where, n = number of terms

a = first term

d = common difference

S_n = sum of n terms

We need to find S₅

(9) 15, 10, 5, . . . In this A.P. sum of first 10 terms is . . .
A. – 75
B. – 125
C. 75
D. 125

Solution:

A. – 75

Explanation:

First term a = 15

Second term t₁ = 10

Third term t₂ = 5

Common difference d = t₂ – t₁ = 5 – 10 = – 5

Number of terms n = 10

Thus, by using sum of n^th term of an A.P. we will find its sum

Where, n = number of terms

a = first term

d = common difference

S_n = sum of n terms

We need to find S₁₀

⇒S₁₀ = 5 [ 30 + 9 × (– 5)]

⇒S₁₀ = 5 [ 30 – 45]

⇒S₁₀ = 5 × (– 15) = – 75

Hence, correct answer is (A)

(10) In an A.P. 1st term is 1 and the last term is 20. The sum of all terms is = 399 then n = . . .
A. 42
B. 38
C. 21
D. 19

Solution:

B. 38

Explanation:

Given, first term = 1

Last term = 20

Sum of n terms, S_n = 399

We need to find number of terms n

Using Sum of n terms of an A.P. formula

2. Find the fourth term from the end in an A.P. – 11, – 8, – 5, . . ., 49.

Solution:

First term from end a = 49

t_n = – 11

t_{n – 1} = – 8

Common difference d = t_n – t_{n – 1}

= – 11 – ( – 8)

= – 11 + 8

= – 3

Now, by using n^th term of an A.P. formula

t_n = a + (n – 1) d

where n = no. of terms

a = first term

d = common difference

t_n = n^th terms

number of terms n = 4

⇒ t₄ = 49 + (4 – 1) × ( – 3)

⇒ t₄ = 49 + 3 × ( – 3)

⇒ t₄ = 49 – 9 = 40

The concepts covered in the chapter Arithmetic Progression can be learnt in depth at BYJU’S. Other beneficial study materials that the students can find to prepare proficiently for the exam are the Maharashtra State Board textbooks and sample papers.