MSBSHSE Solutions For Class 9 Maths Part 1 Chapter 7 Statistics are considered to be very useful when you are preparing for the Class 9 Maths exams. Here, we bring to you detailed answers to the exercises of Chapter 7 Statistics. Subject matter experts who created the solutions have collected these questions for you to revise from the chapter 7 of 9th Maths Maharashtra Board Textbook. This chapter of Maharashtra State Board Class 9 Solutions deals with sub-divided bar-diagram, Grouped and ungrouped frequency distribution, Percentage bar-diagram, Cumulative frequency distribution, Primary and secondary data, Mean, Median and Mode for ungrouped data and data collection.
Download the PDF of Maharashtra Solutions For Class 9 Maths Part 1 Chapter 7 Statistics
Access answers to Maths MSBSHSE Solutions For Class 9 Part 1 Chapter 7 – Statistics
Practice set 7.1 Page no: 111
1. The following table shows the number of Buses and Trucks in nearest lakh units. Draw percentage bar-diagram. (Approximate the percentages to the nearest integer)
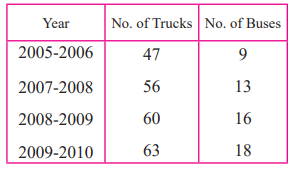
Solution:
To draw percentage bar diagram, we find the % of buses and trucks with respect to total number of vehicles for each year.
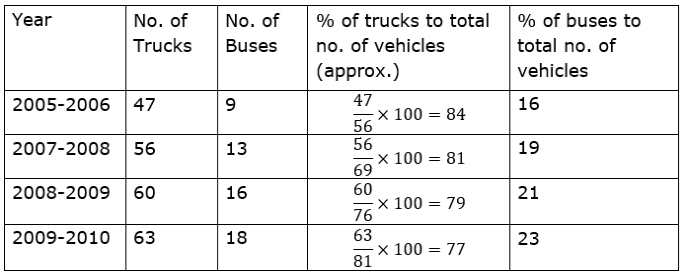
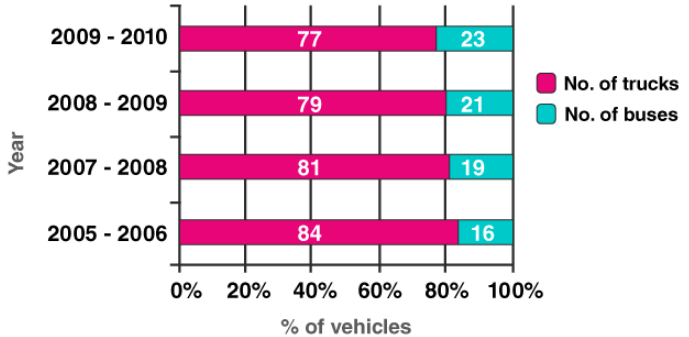
According to the data of above table, the percentage bar diagram shown below.
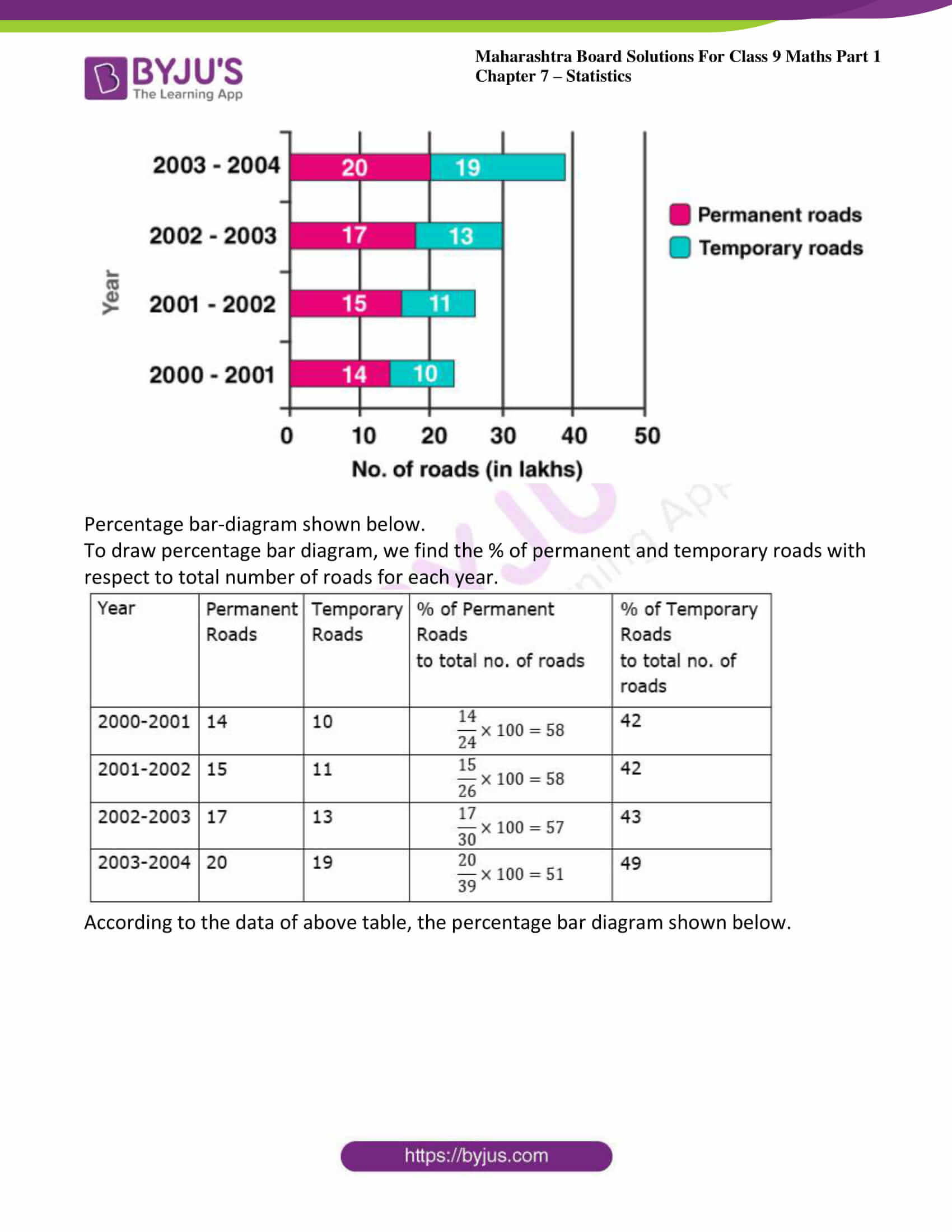
2. In the table given below, the information is given about roads. Using this draw sub-divided and percentage bar diagram (Approximate the percentages to the nearest integer)
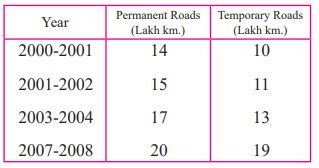
Solution:
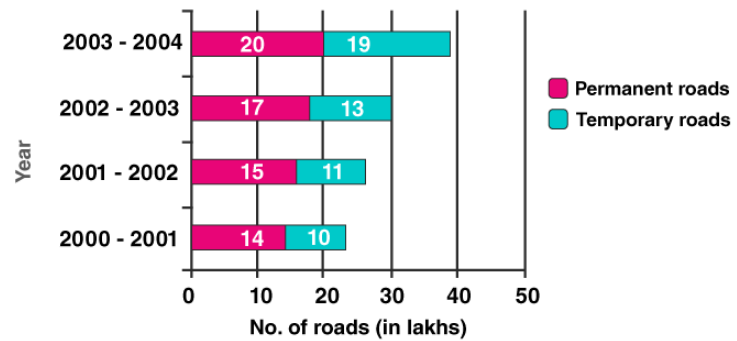
Sub divided bar diagram shown below.
To draw sub divided bar diagram, we use the given table for each year.
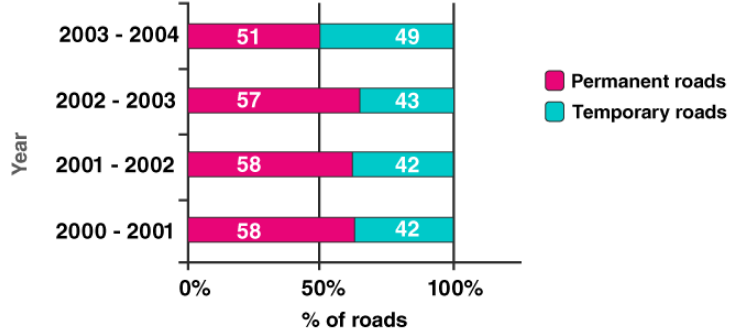
Percentage bar-diagram shown below.
To draw percentage bar diagram, we find the % of permanent and temporary roads with respect to total number of roads for each year.
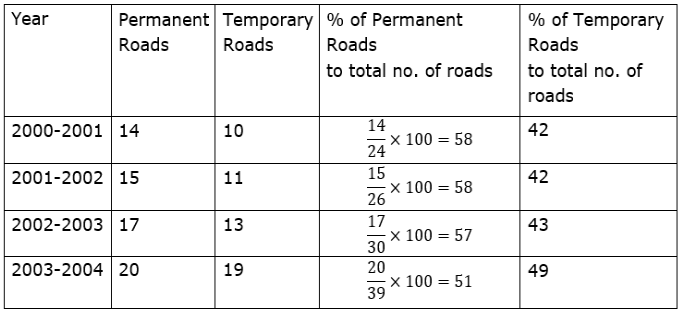
According to the data of above table, the percentage bar diagram shown below.
Practice set 7.2 Page no: 113
1. Classify following information as primary or secondary data.
i. Information of attendance of every student collected by visiting every class in a school.
ii. The information of heights of students was gathered from school records and sent to the head office, as it was to be sent urgently.
iii. In the village Nandpur, the information collected from every house regarding students not attending school.
iv. For science project, information of trees gathered by visiting a forest.
Solution:
i. Primary data, because the data is collected by the investigator himself by going in every class.
ii. Secondary data, because the data is collected by some other person and is being used by investigator.
iii. Primary data, because the data is collected by the investigator himself by visiting every house.
iv. Primary data, because the data is collected by the investigator himself by visiting forest.
Practice set 7.3 Page no: 118
1. For class interval 20-25 write the lower-class limit and the upper-class limit.
Solution:
For class interval 20-25,
Lower class limit = 20
Upper class limit = 25
2. Find the class-mark of the class 35-40.
Solution:

3. If class mark is 10 and class width is 6 then find the class.
Solution:
We know that
Class size = upper limit – lower limit
⇒ Upper limit – lower limit = 6 …… (1)
Also, we know that

⇒ Lower limit + upper limit = 2× 10
⇒ Lower limit + upper limit = 20 …. (2)
Adding (1) and (2)
⇒ 2(Upper limit) = 26
⇒ Upper limit = 13
And lower limit = 7
⇒ Class = 7-13
4. Complete the following table.
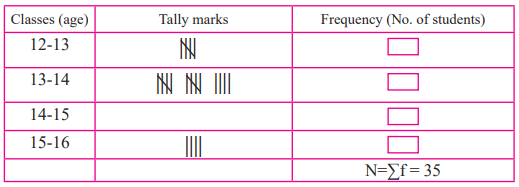
Solution:
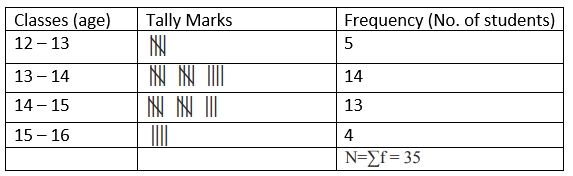
For class 14-15:
Frequency = 35 – (4 + 14 + 4)
= 35 – 22 = 13
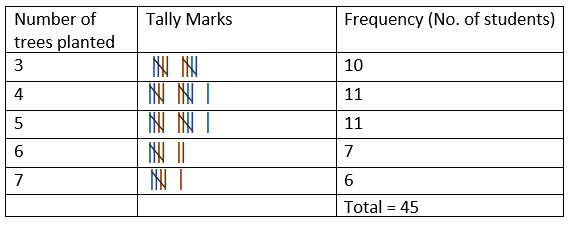
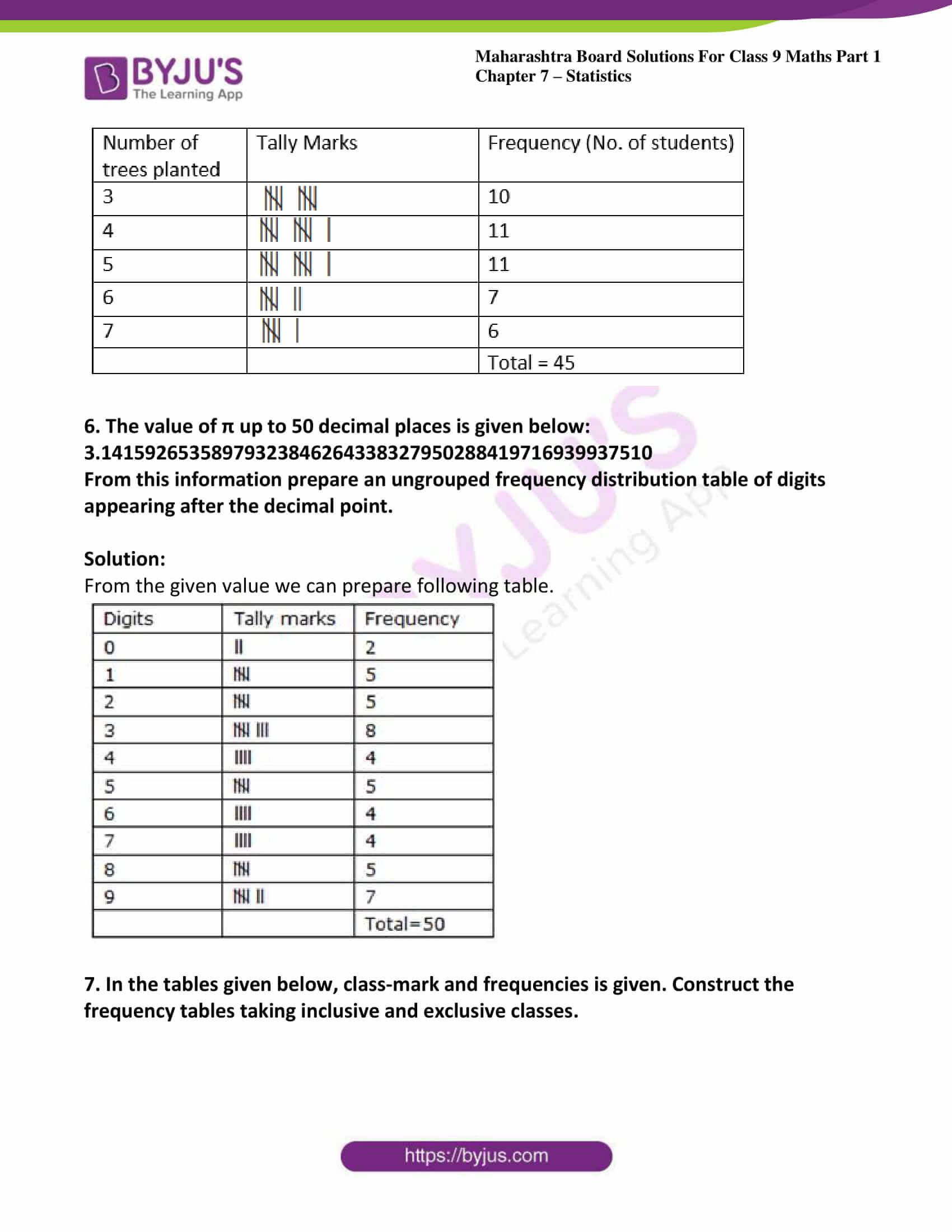
5. In a ‘tree plantation’ project of a certain school there are 45 students of ‘HaritSena.’ There cord of trees planted by each student is given below :
3, 5, 7, 6, 4, 3, 5, 4, 3, 5, 4, 7, 5 , 3, 6, 6, 5, 3, 4, 5, 7, 3, 5, 6, 4, 4, 3,5, 6, 6, 4, 3, 5, 7, 3, 4, 5, 7, 6, 4, 3, 5, 4, 4, 7.
Prepare a frequency distribution table of the data.
Solution:
Arrange the data in ascending order.
3,3,3,3,3,3,3,3,3,3,4,4,4,4,4,4,4,4,4,4,4,5,5,5,5,5,5,5,5,5,5,5,6,6,6,6,6,6,6,7,7,7,7,7,7
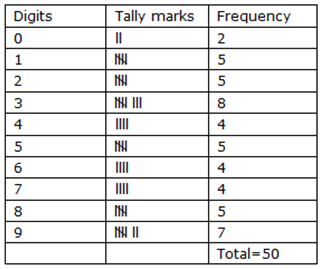
6. The value of π up to 50 decimal places is given below:
3.14159265358979323846264338327950288419716939937510
From this information prepare an ungrouped frequency distribution table of digits appearing after the decimal point.
Solution:
From the given value we can prepare following table.
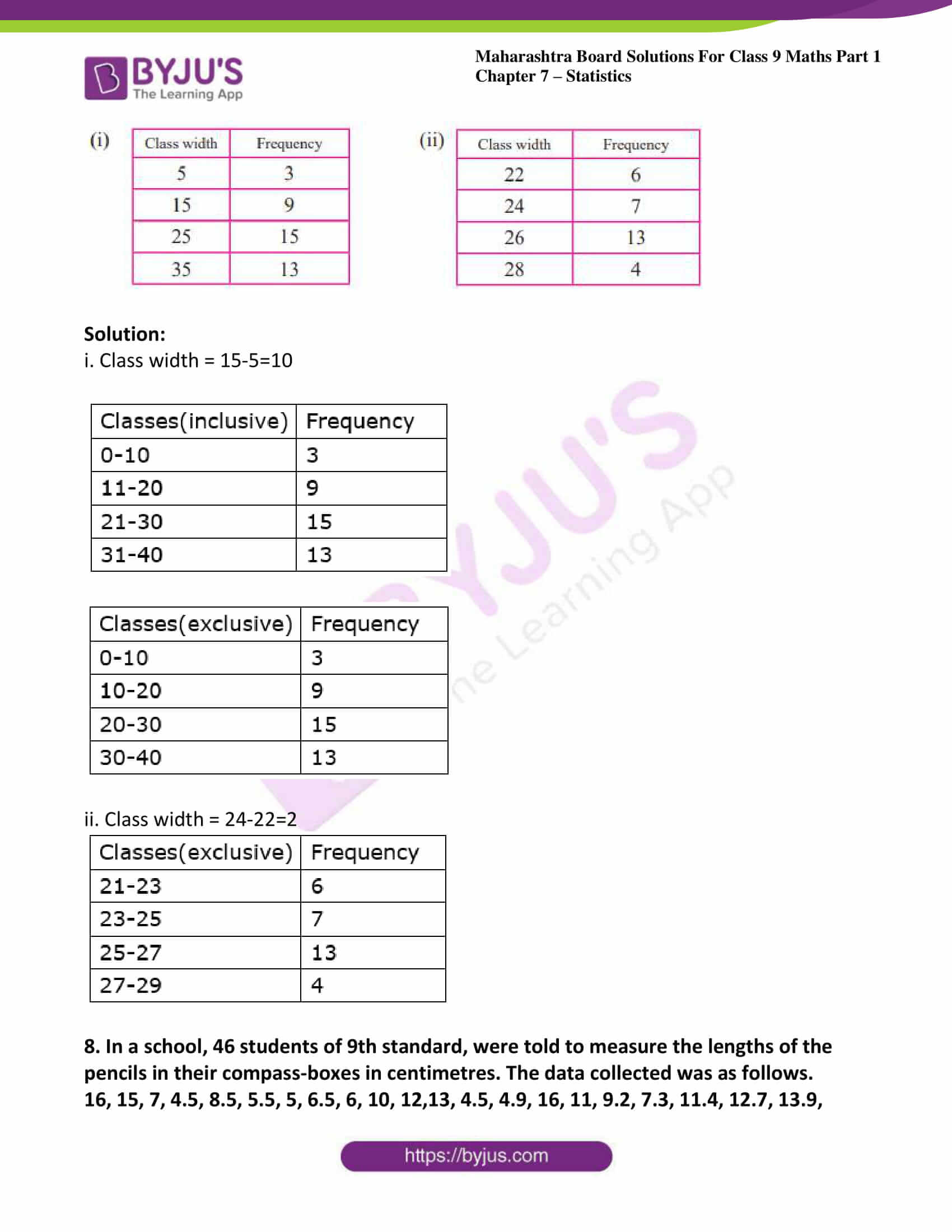
7. In the tables given below, class-mark and frequencies is given. Construct the frequency tables taking inclusive and exclusive classes.
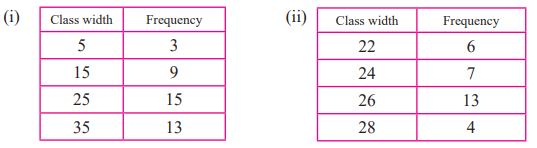
Solution:
i. Class width = 15-5=10
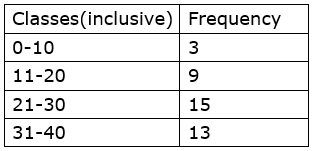
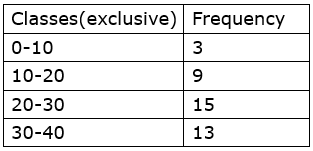
ii. Class width = 24-22=2
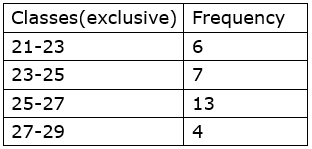
8. In a school, 46 students of 9th standard, were told to measure the lengths of the pencils in their compass-boxes in centimetres. The data collected was as follows.
16, 15, 7, 4.5, 8.5, 5.5, 5, 6.5, 6, 10, 12,13, 4.5, 4.9, 16, 11, 9.2, 7.3, 11.4, 12.7, 13.9, 16,5.5, 9.9, 8.4, 11.4, 13.1, 15, 4.8, 10, 7.5, 8.5, 6.5,7.2, 4.5, 5.7, 16, 5.7, 6.9, 8.9, 9.2, 10.2, 12.3, 13.7,14.5, 10
By taking inclusive classes 0-5, 5-10, 10-15….Prepare a grouped frequency distribution table.
Solution:
From the given values we can prepare following table.

Practice set 7.4 Page no: 121
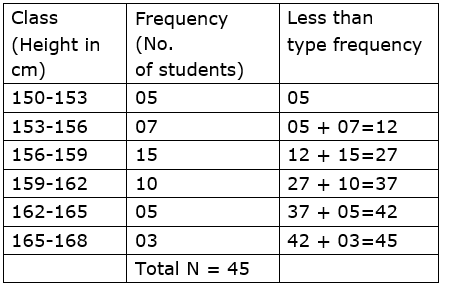
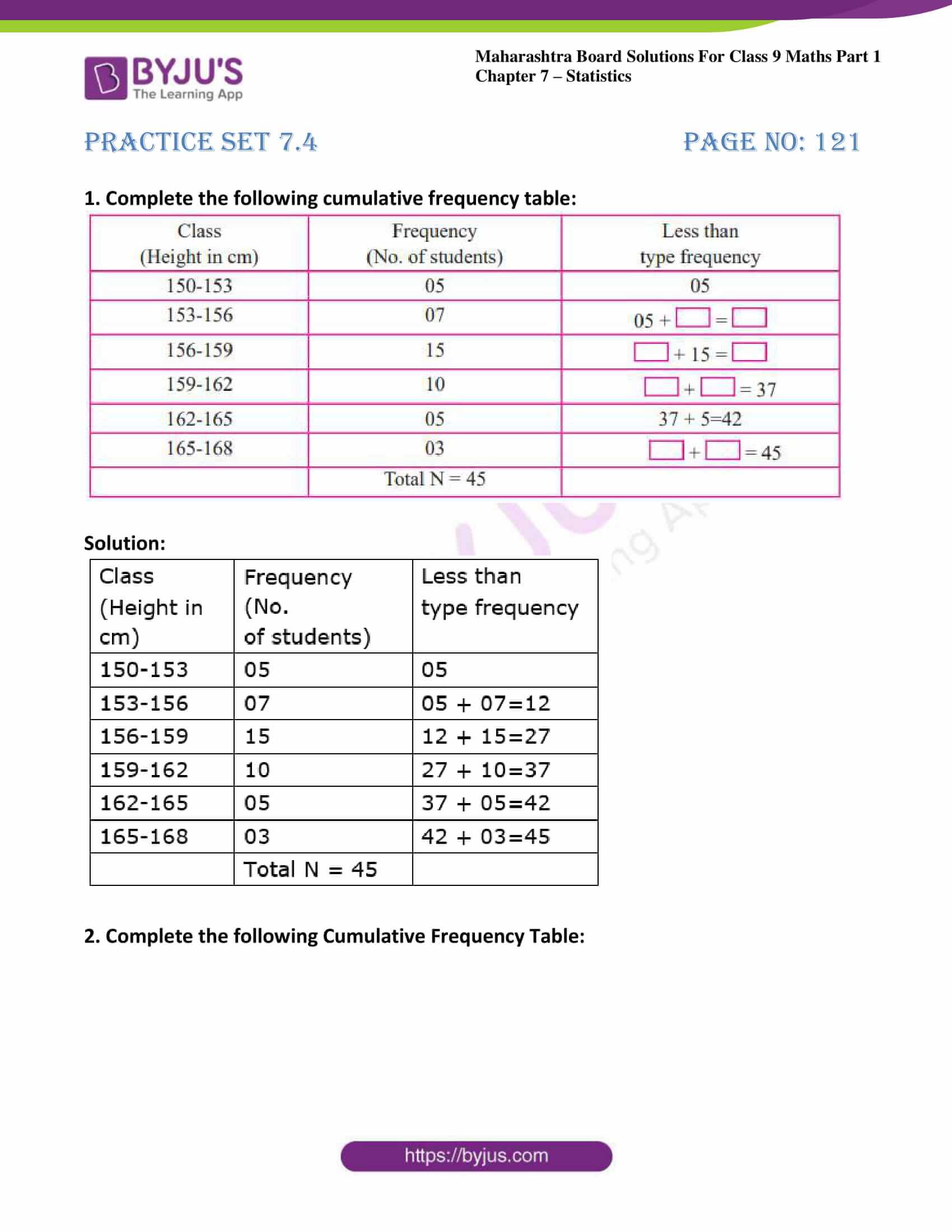
1. Complete the following cumulative frequency table:
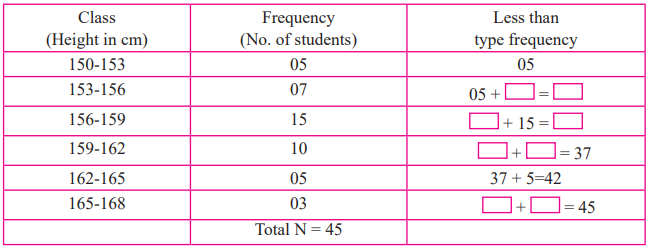
Solution:
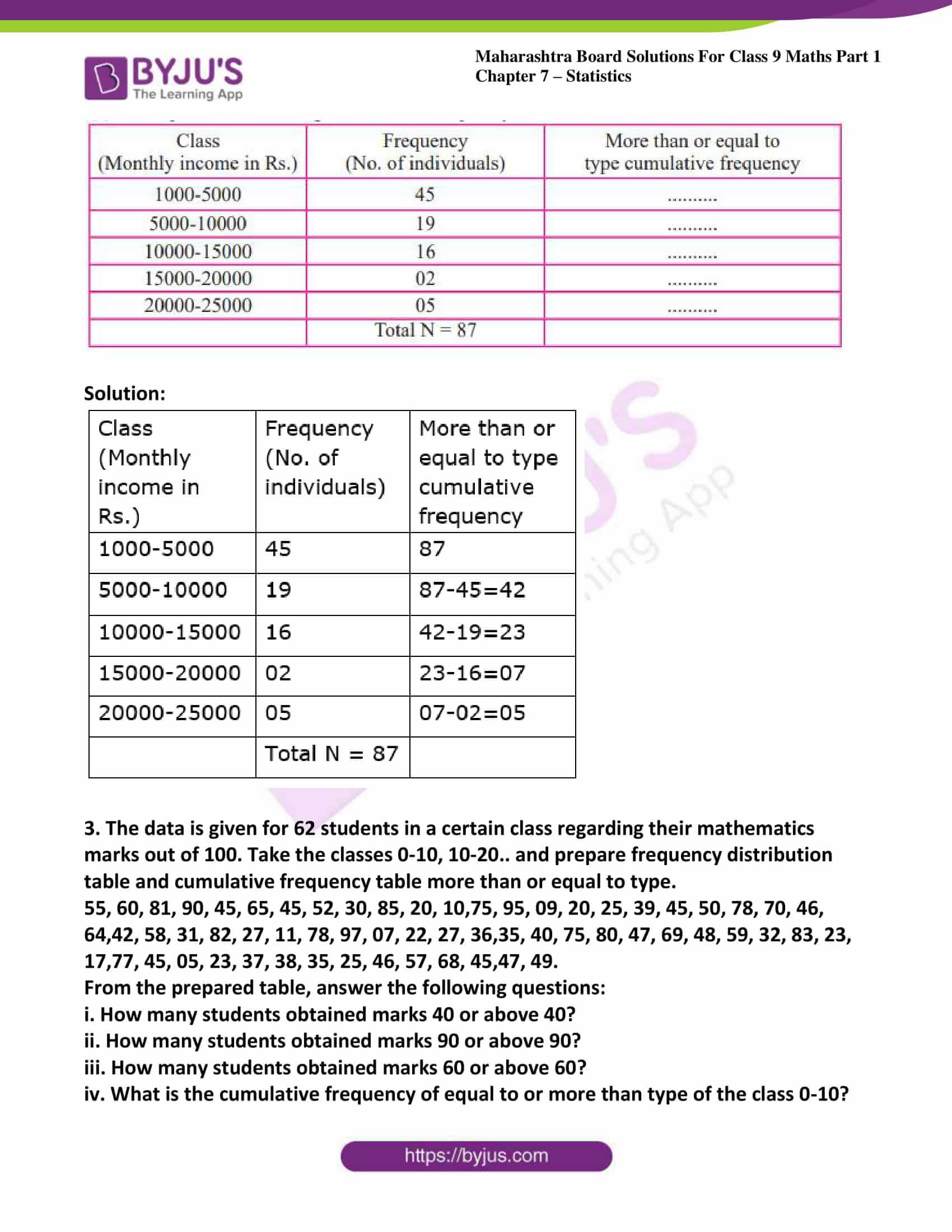
2. Complete the following Cumulative Frequency Table:
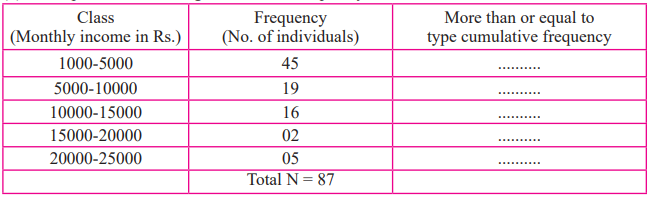
Solution:
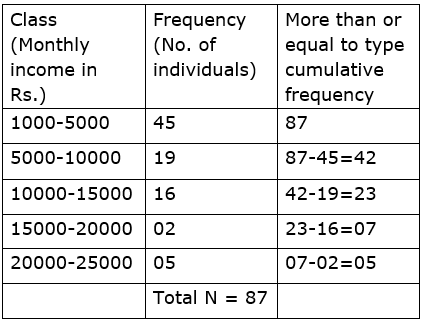
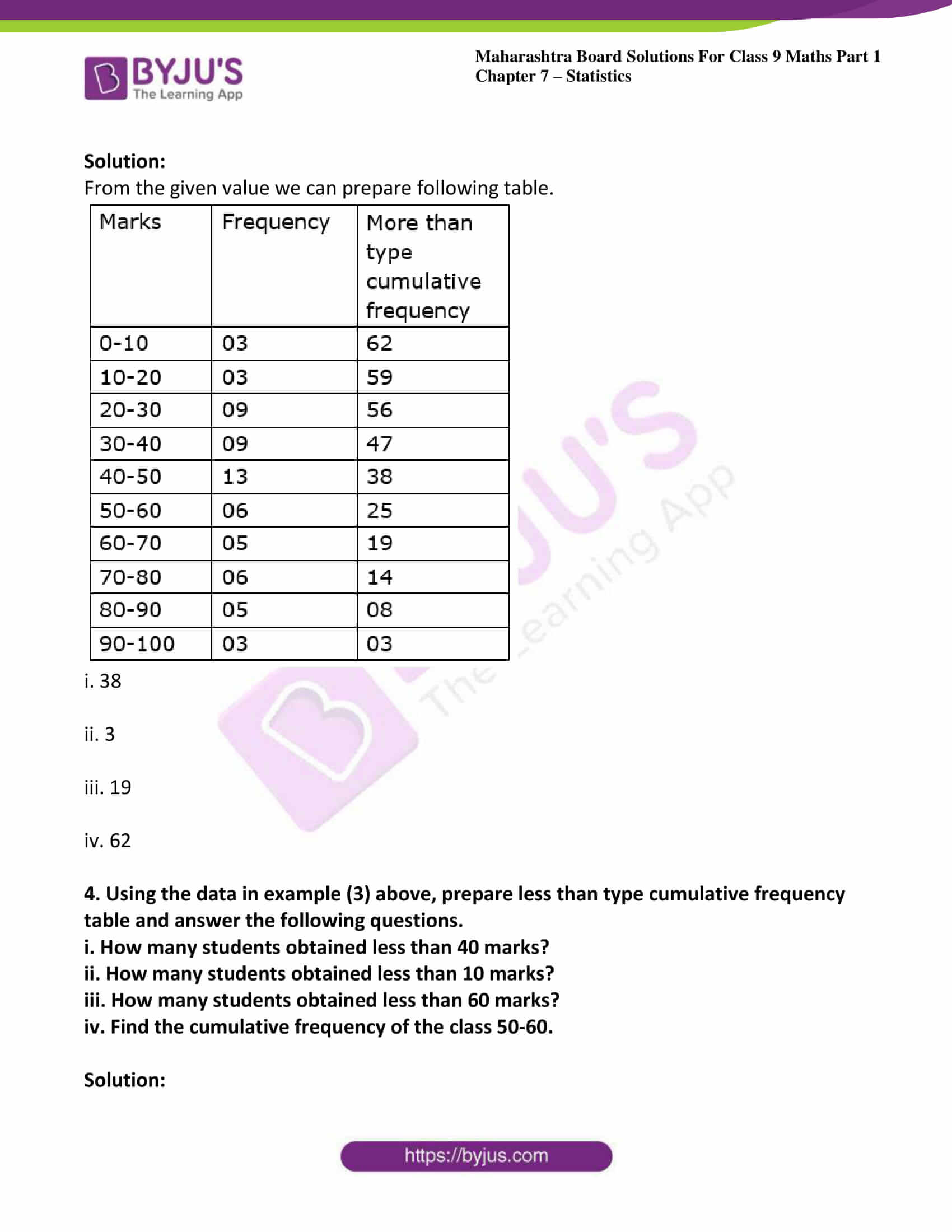
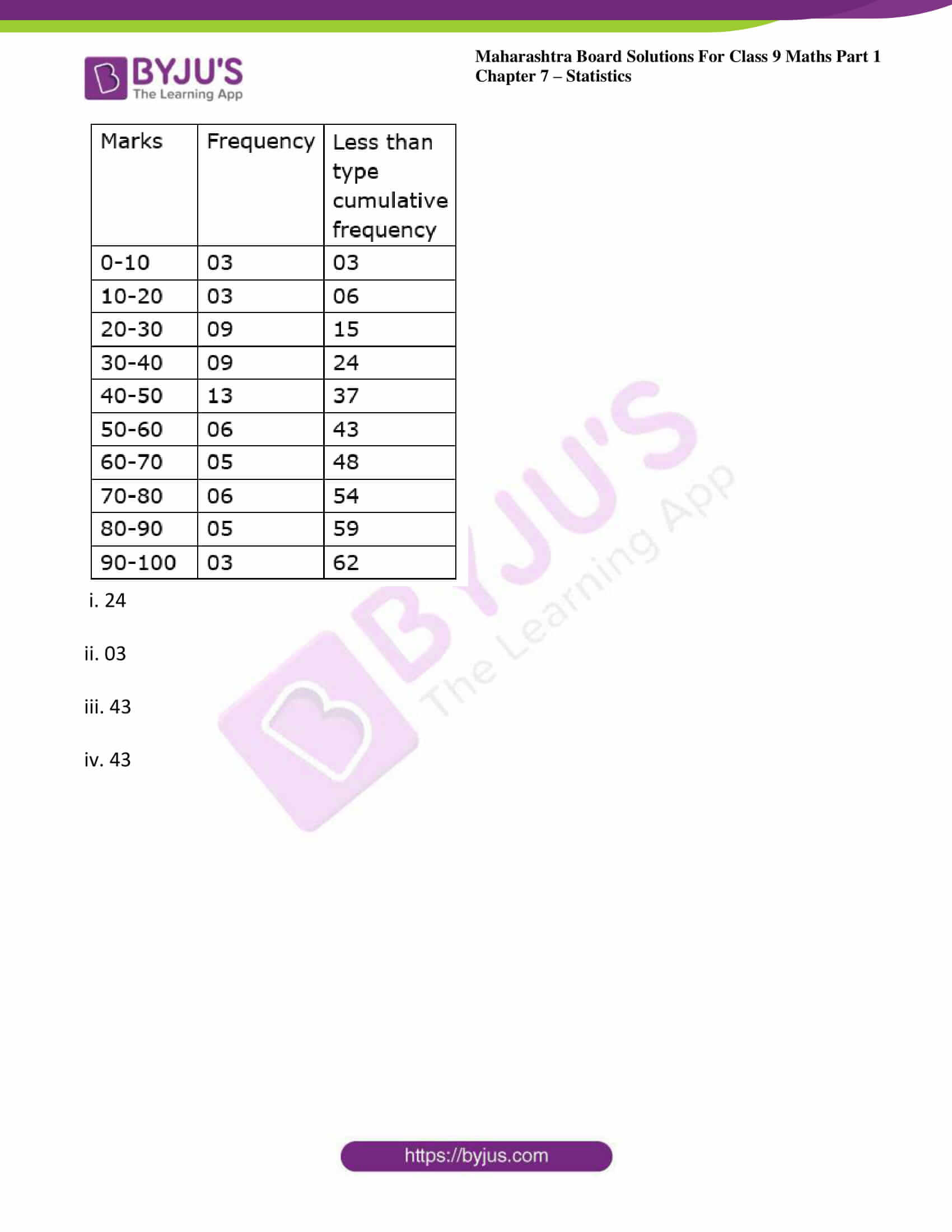
3. The data is given for 62 students in a certain class regarding their mathematics marks out of 100. Take the classes 0-10, 10-20.. and prepare frequency distribution table and cumulative frequency table more than or equal to type.
55, 60, 81, 90, 45, 65, 45, 52, 30, 85, 20, 10,75, 95, 09, 20, 25, 39, 45, 50, 78, 70, 46, 64,42, 58, 31, 82, 27, 11, 78, 97, 07, 22, 27, 36,35, 40, 75, 80, 47, 69, 48, 59, 32, 83, 23, 17,77, 45, 05, 23, 37, 38, 35, 25, 46, 57, 68, 45,47, 49.
From the prepared table, answer the following questions:
i. How many students obtained marks 40 or above 40?
ii. How many students obtained marks 90 or above 90?
iii. How many students obtained marks 60 or above 60?
iv. What is the cumulative frequency of equal to or more than type of the class 0-10?
Solution:
From the given value we can prepare following table.
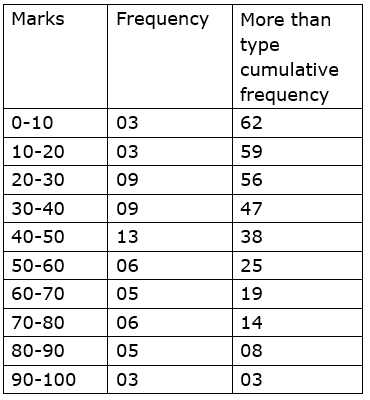
i. 38
ii. 3
iii. 19
iv. 62
4. Using the data in example (3) above, prepare less than type cumulative frequency table and answer the following questions.
i. How many students obtained less than 40 marks?
ii. How many students obtained less than 10 marks?
iii. How many students obtained less than 60 marks?
iv. Find the cumulative frequency of the class 50-60.
Solution:

i. 24
ii. 03
iii. 43
iv. 43
Practice set 7.5 Page no: 125
1. Yield of soyabean per acre in quintal in Mukund’s field for 7 years was 10, 7, 5, 3, 9, 6, 9. Find the mean of yield per acre.
Solution:

2. Find the median of the observations, 59, 75, 68, 70, 74, 75, 80.
Solution:
Given: 59, 75, 68, 70, 74, 75, 80.
Here, n =7
On arranging the data in ascending order,
59, 68, 70, 74, 75, 75, 80
When the number of terms of odd, the median is given as:
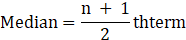
⇒ Median =
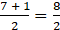
⇒ Median = 4th term
∴ Median =74
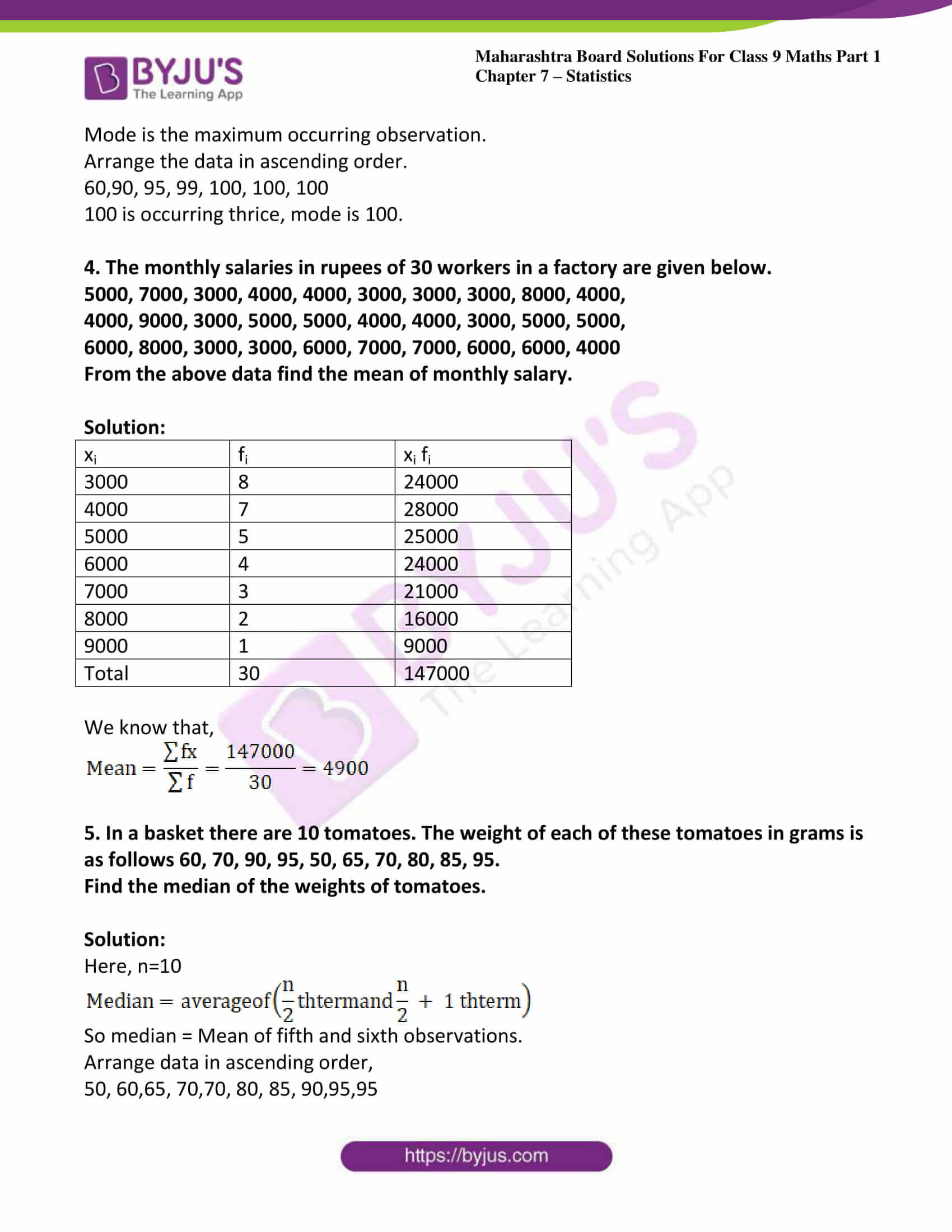
3. The marks (out of 100) obtained by 7 students in Mathematics’ examination are given below. Find the mode for these marks.
99, 100, 95, 100, 100, 60, 90
Solution:
Mode is the maximum occurring observation.
Arrange the data in ascending order.
60,90, 95, 99, 100, 100, 100
100 is occurring thrice, mode is 100.
4. The monthly salaries in rupees of 30 workers in a factory are given below.
5000, 7000, 3000, 4000, 4000, 3000, 3000, 3000, 8000, 4000,
4000, 9000, 3000, 5000, 5000, 4000, 4000, 3000, 5000, 5000,
6000, 8000, 3000, 3000, 6000, 7000, 7000, 6000, 6000, 4000
From the above data find the mean of monthly salary.
Solution:
| xi | fi | xi fi |
| 3000 | 8 | 24000 |
| 4000 | 7 | 28000 |
| 5000 | 5 | 25000 |
| 6000 | 4 | 24000 |
| 7000 | 3 | 21000 |
| 8000 | 2 | 16000 |
| 9000 | 1 | 9000 |
| Total | 30 | 147000 |
We know that,

5. In a basket there are 10 tomatoes. The weight of each of these tomatoes in grams is as follows 60, 70, 90, 95, 50, 65, 70, 80, 85, 95.
Find the median of the weights of tomatoes.
Solution:
Here, n=10
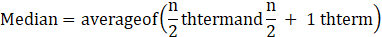
So median = Mean of fifth and sixth observations.
Arrange data in ascending order,
50, 60,65, 70,70, 80, 85, 90,95,95
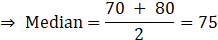
6. A hockey player has scored following number of goals in 9 matches.
5, 4, 0, 2, 2, 4, 4, 3, 3. Find the mean, median and mode of the data.
Solution:

7. The calculated mean of 50 observations was 80. It was later discovered that observation 19 was recorded by mistake as91. What was the correct mean?
Solution:
We know that
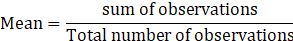
⇒ Sum of observations = Mean ×Total number of observations
Given mean of 50 observations = 80
⇒ Sum of 50 observations=80×50
⇒ Sum of 50 observations =4000
For correct mean, we will subtract 91 and add 19 to the sum.
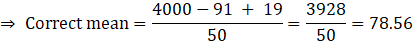
8. Following 10 observations are arranged in ascending order as follows.
2, 3, 5, 9, x + 1, x + 3, 14, 16, 19, 20
If the median of the data is 11, find the value of x.
Solution:
Here, n=10

So median = Mean of fifth and sixth observations.
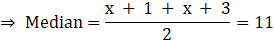
⇒ 2x + 4=22
⇒ x=9
9. The mean of 35 observations is 20, out of which mean of first 18 observations is 15and mean of last 18 observation is 25. Find the 18th observation.
Solution:
We know that
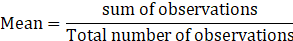
⇒ Sum of observations = Mean ×Total number of observations
Sum of 35 observations = 20×35=700
Sum of first 18 observations = 15×18=270
Sum of last 18 observations = 25× 18=450
While adding first 18 observations and last 18 observations, we add 18th observation twice so,
18th observation= Sum of first 18 observations + Sum of last 18 observations – Sum of 35 observations
⇒ 18th observation= 270 + 450 – 700 =20
10. The mean of 5 observations is 50. One of the observations was removed from the data, hence the mean became 45. Find the observation which was removed.
Solution:
We know that
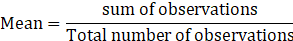
⇒ Sum of observations = Mean ×Total number of observations
Sum of 5 observations = 50×5=250
Sum after removing one observation = 4×45=180
⇒ Removed observation = sum of 5 observations – Sum after removing one observation
⇒ Removed observation = 250 -180 =70
11. There are 40 students in a class, out of them 15 are boys. The mean of marks obtained by boys is 33 and that for girls is 35. Find out the mean of all students in the class.
Solution:
We know that
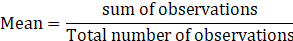
⇒ Sum of observations = Mean ×Total number of observations
Mean of marks obtained by 15 boys = 33
⇒ Total marks obtained by boys = 33×15=495
Number of girls = 40 – 15=25
And Mean of marks obtained by 25 girls = 35
⇒ Total marks obtained by girls = 35×25=8755
Total marks obtained by class = Total marks obtained by boys and girls = 495 + 875
=1370

12. The weights of 10 students (in kg) are given below:
40, 35, 42, 43, 37, 35, 37, 37, 42, 37. Find the mode of the data.
Solution:
Mode is the maximum occurring observation.
Arrange the data in ascending order.
35, 35, 37, 37, 37, 37, 40, 42, 42,43
37 occurs four times.
Mode = 37kg
13. In the following table, the information is given about the number of families and the siblings in the families less than 14 years of age. Find the mode of the data.

Solution:
From the data, we observe that 25 families have 2 siblings which is the highest so mode is 2 siblings.
14. Find the mode of the following data.

Solution:
From the data, we observe that 9 students have got 35 and 37 marks which is the highest so mode is 35 and 37 marks.
Problem set 7 Page no: 126
1. Write the correct alternative answer for each of the following questions.
i. Which of the following data is not primary?
A. By visiting a certain class, gathering information about attendance of students.
B. By actual visit to homes, to find number of family members.
C. To get information regarding plantation of soybean done by each farmer from the village Talathi.
D. Review the cleanliness status of canals by actually visiting them.
Solution:
C. To get information regarding plantation of soybean done by each farmer from the village Talathi.
Explanation:
In option C, investigator is not collecting the data himself but using the data collected by the farmers.
ii. What is the upper-class limit for the class 25-35?
A. 25
B. 35
C. 60
D. 30
Solution:
B. 35
Explanation:
In the class 25-35, 35 is the upper-class limit.
iii. What is the class-mark of class 25-35?
A. 25
B. 35
C. 60
D. 30
Solution:
D. 30
Explanation:
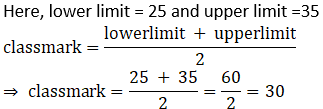
iv. If the classes are 0-10, 10-20, 20-30… then in which class should the observation 10be included?
A. 0-10
B. 10-20
C. 0-10 and 10-20 in these 2 classes
D. 20-30
Solution:
B. 10 – 20
Explanation:
These classes are exclusive in nature which means the classes are continuous. The class 0-10 include 0 and all the numbers less than 10 while class 10 – 20 include 10 and all the numbers less than 20 and so on.
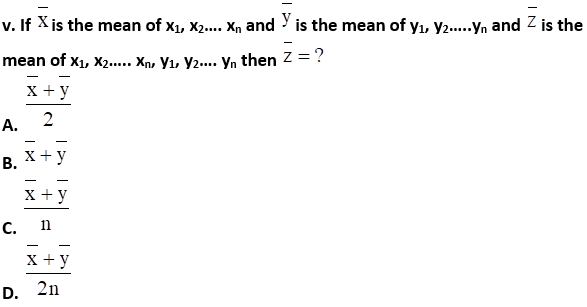
Solution:
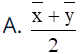
Explanation:
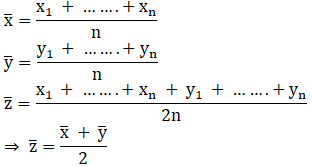
vi. The mean of five numbers is 80, out of which mean of 4 numbers is 46, find the 5th number:
A. 4
B. 20
C. 434
D. 66
Solution:
D. 66
Explanation:
5th number = Sum of five numbers – Sum of four numbers
= (5 x 50) – (4 x 46)
= 250 – 184
= 66
vii. Mean of 100 observations is 40. The 9th observation is 30. If this is replaced by70 keeping all other observations same, find the new mean.
A. 40.6
B. 40.4
C. 40.3
D. 40.7
Solution:
B. 40.4
Explanation:
We know that
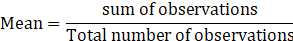
⇒ Sum of observations = Mean × Total number of observations
⇒ Sum of 100 observations = 40×100 = 4000
For new mean, we will subtract 30 and add 70 to the sum.
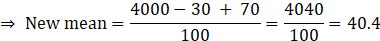
viii. What is the mode of 19, 19, 15, 20, 25, 15, 20, 15?
A. 15
B. 20
C. 19
D. 25
Solution:
A. 15
Explanation:
Mode is the most frequently occurring observation. On arranging above data in ascending order, we get: 15, 15, 15, 19, 19, 20, 20, 25. Hence, 15 is the mode as it has the highest frequency(3 times)
ix. What is the median of 7, 10, 7, 5, 9, 10?
A. 7
B. 9
C. 8
D. 10
Solution:
C. 8
Explanation:
Here, n=6

So median = Mean of third and fourth observations.
On arranging above data in ascending order, we get: 5, 7,7,9,10,10
⇒ 3rd term = 7 and 4th term = 9
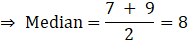
x. From following table, what is the cumulative frequency of less than type for the class 30-40?

A. 13
B. 15
C. 35
D. 22
Solution:
C. 35
Explanation:
Cumulative Frequency of less than type of the 30-40= sum of the frequencies of all the classes upto 30-40
⇒ Required cumulative frequency =7 + 3 + 12 + 13=35
2. The mean salary of 20 workers is Rs.10, 250. If the salary of office superintendent is added, the mean will increase by Rs.750. Find the salary of the office superintendent.
Solution:
We know that,
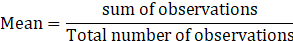
⇒ Sum of salary of 20 workers= 20×10250 …(1)
And Mean increases by 750 when salary of superintendent is also added to it.
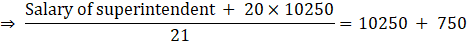
⇒ Salary of superintendent + 20×10250 = 11000 × 21
⇒ Salary of superintendent =231000 – 205000
⇒ Salary of superintendent =26000
3. The mean of nine numbers is 77. If one more number is added to it than the mean increases by 5. Find the number added in the data.
Solution:
We know that

⇒ Sum of observations = Mean × Total number of observations
⇒ Sum of 9 numbers = 9×77 ..(1)
And Mean increases by 5 when one more number is also added to it.
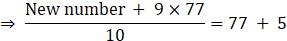
⇒ New number + 9×77 = 82 × 5
⇒ New number =820 – 693 = 127
4. The monthly maximum temperature of a city is given in degree celcius in the following data. By taking suitable classes, prepare the grouped frequency distribution table
29.2, 29.0, 28.1, 28.5, 32.9, 29.2, 34.2, 36.8, 32.0, 31.0,
30.5, 30.0, 33, 32.5, 35.5, 34.0, 32.9, 31.5, 30.3, 31.4,
30.3, 34.7, 35.0, 32.5, 33.5, 29.0, 29.5, 29.9, 33.2, 30.2
From the table, answer the following questions.
i. For how many days the maximum temperature was less than 34oC?
ii. For how many days the maximum temperature was 34oC or more than 34oC?
Solution:
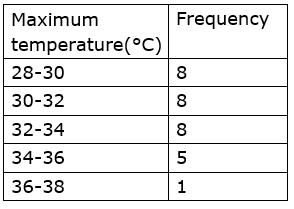
(i) Less than 34°C =8 + 8 + 8=24
(ii) Equal to or more than 34°C=5 + 1=6
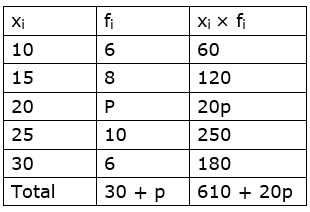
5. If the mean of the following data is 20.2, then find the value of p.
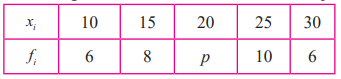
Solution:
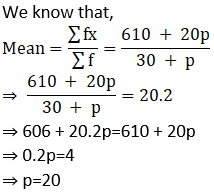
6. There are 68 students of 9th standard from model Highschool, Nandpur. They have scored following marks out of 80, in written exam of mathematics.
70, 50, 60, 66, 45, 46, 38, 30, 40, 47, 56, 68,80, 79, 39, 43, 57, 61, 51, 32, 42, 43, 75, 43,36, 37, 61, 71, 32, 40, 45, 32, 36, 42, 43, 55,56, 62, 66, 72, 73, 78, 36, 46, 47, 52, 68, 78,80, 49, 59, 69, 65, 35, 46, 56, 57, 60, 36, 37,45, 42, 70, 37, 45, 66, 56, 47
By taking classes 30-40, 40-50, …. prepare the less than type cumulative frequency table Using the table, answer the following questions:
i. How many students, have scored marks less than 80?
ii. How many students have scored marks less than 40?
iii. How many students have scored marks less than 60?
Solution:
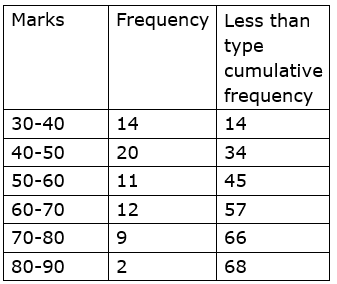
i. 66
ii. 14
iii. 45
7. By using data in example (6), and taking classes 30-40, 40-50… prepare equal to or more than type cumulative frequency table and answer the following questions based on it.
i. How many students have scored marks 70 or more than 70?
ii. How many students have scored marks 30 or more than 30?
Solution:
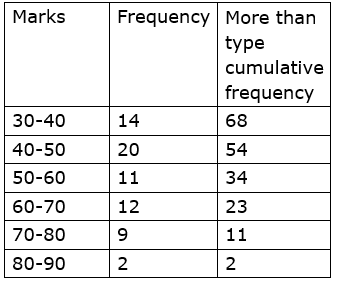
i. 11
ii. 68
8. There are 10 observations arranged in ascending order as given below.
45,47,50,52, x, x + 2, 60,62,63,74. The median of these observations is 53.
Find the value of x. Also find the mean and the mode of the data.
Solution:


The Mean, Median and Mode are the arithmetic average of a data set. This is found by adding the numbers in a data set and dividing by how many numbers there are. The median is the middle number in a data set when the numbers are listed in either ascending or descending order. The mode is the value that occurs the most often in a data set, and the range is the difference between the highest and lowest values in a data set. To know more about these concepts stay tuned with BYJU’S.
Frequently Asked Questions on Maharashtra State Board Solutions for Class 9 Maths Part 1 Chapter 7 Statistics
Are these Maharashtra Board Class 9 Solutions useful to prepare for the exams?
Yes, these solutions can be very helpful. Students are highly recommended to practise these solutions after revising the subjects, as they set the basis for the questions that could get asked often in the board exams.
How are these Maharashtra State Board Class 9 Maths Part 1 Chapter 7 Statistics Solutions helpful?
Students are encouraged to download these solutions and practise them. Then they can refer back to the solutions to analyse their performance. This will also help them to rectify their mistakes and to avoid making them during the board exams.
How can we find these Maharashtra Board Class 9 Solutions?
Yes, we provide the solutions to download. We have also provided the solutions as a scrollable PDF and we have also mentioned the clickable link for the students to access. Meanwhile, the questions and the solutions are also available online on our webpage.























Comments