In statistics and probability, any subset, say A of a sample space S, is called an event. Also, we can define the occurrence and non-occurrence of an event A as:
- If the outcome ω of the experiment is such that ω ∈ A, where A is an event in sample space S, then we can say that event A has occurred.
- If the outcome ω is such that ω ∉ A, we say, that event A has not occurred.
Based on the elements they have, we can classify different types of events in probability, such as simple events, sure events, impossible events, etc. In this article, you will learn what are exhaustive events, representation of exhaustive events in probability with examples.
Go through the exhaustive events definition along with the representation of the exhaustive set of events.
Exhaustive Events Meaning
If E1, E2, E3, …,En are n events of a sample space S, and if:
then E1, E2, E3, …,En are called exhaustive events.
In other words, events E1, E2, E3, …,En are called exhaustive events if at least one of them necessarily occurs whenever the experiment is performed.
| Read more: |
What are Exhaustive Events in Probability?
Let us consider the experiment of throwing a die.
Sample space S = {1, 2, 3, 4, 5, 6}
Assume that A, B and C are the events associated with this experiment. Also, let us define these events as:
A be the event of getting a number greater than 3
B be the event of getting a number greater than 2 but less than 5
C be the event of getting a number less than 3
We can write these events as:
A = {4, 5, 6}
B = {3, 4}
and C = {1, 2}
We observe that
A ⋃ B ⋃ C = {4, 5, 6} ⋃ {3, 4} ⋃ {1, 2} = {1, 2, 3, 4, 5, 6} = S
Therefore, A, B, and C are called exhaustive events.
However, the probability of exhaustive events is equal to 1.
Collectively Exhaustive Events
In probability theory, a set of events can be either jointly or collectively exhaustive if at least one of the events must occur for sure. We can verify that because the outcomes comprise the entire range of possible outcomes, i.e. sample space for an experiment. For example, when throwing an unbiased six-sided die, the outcomes 1, 2, 3, 4, 5, and 6 are collectively exhaustive. Similarly, when a coin is tossed, the outcome can either be heads or tails. Therefore, considering each can occur during an experiment, they are both described as exhaustive events. However, the union of all those events comprises the sample space of that experiment known as the exhaustive events.
Mutually Exclusive and Exhaustive Events
If Ei ∩ Ej = φ for i ≠ j i.e., events Ei and Ej are pairwise disjoint and
Also, read: Mutually exclusive events
Exhaustive Events Venn Diagram
The below figure shows the Venn diagram representation of collectively exhaustive events in comparison with exclusive events.
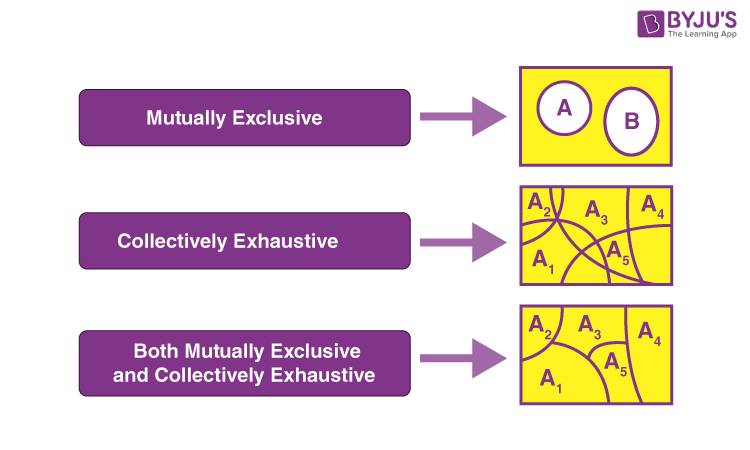
Go through the solved examples given below to understand the concept clearly.
Exhaustive Events in Probability with Examples
Example 1:
In an experiment, three coins are tossed at a time, consider the following events.
A: ‘No tail appears’,
B: ‘Exactly one tail appears’
C: ‘At least two tails appear’
Do they form a set of exhaustive events?
Solution:
In the experiment of tossing a coin three times or three coins tossed at a time, the outcomes will be the same, i.e. the sample space constitutes the same outcomes in both the cases.
Thus,
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
As per the given,
Event A: ‘No tail appears’
That means only heads will appear.
So, A = {HHH}
Event B: ‘Exactly one tail appears’
So, B = {HHT, HTH, THH}
Event C: ‘At least two tails appear’
That means, two tails and more than two tails can be considered.
So, C = {HTT, THT, TTH, TTT}
Now,
A ∪ B ∪ C = {HHH} ∪ {HHT, HTH, THH} ∪ {HTT, THT, TTH, TTT}
= {TTT, HTT, THT, TTH, HHT, HTH, THH, HHH}
= S
Therefore, A, B and C are exhaustive events.
Example 2:
Consider the set of first 10 natural numbers. Check if the following defined events are exhaustive.
A: Selecting a prime number
B: Selecting a multiple of 2
C: Choosing a perfect square number
Solution:
Sample space = Set of first 10 natural numbers
i.e. S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Given that,
A is the event of selecting a prime number.
So, A = {2, 3, 5, 7}
B is the event of selecting a multiple of 2.
So, B = {2, 4, 6, 8, 10}
C is the event of choosing a perfect square number.
So, C = {1, 4, 9}
Now,
A ∪ B ∪ C = {2, 3, 5, 7} ∪ {2, 4, 6, 8, 10} ∪ {1, 4, 9}
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
= S
Hence, the given set of events are exhaustive.
Frequently Asked Questions – FAQs
What is the meaning of exhaustive events?
A set of events are called exhaustive events if at least one of them necessarily occurs whenever the experiment is performed. Also, the union of all these events constitutes the sample space of that experiment.
What does it mean when two events are exhaustive?
Two events are exhaustive when their union is equal to the sample space.
What is the difference between mutually exclusive and exhaustive events? Explain with an example.
If A ∩ B = φ for i.e., events A and B are disjoint and A ∪ B = S, then events A and B are called mutually exclusive and exhaustive events. For example, in an experiment of rolling a die, the events denoting the occurrence of even and odd numbers are disjoint yet they cover all the outcomes of the sample space when we take union of these events.
Are all exhaustive events mutually exclusive?
No, all exhaustive events may or may not be mutually exclusive.
Can events be exhaustive and independent?
Yes, events are exhaustive and independent. Suppose two events A and B are exhaustive, i.e. A ∪ B = S are also can be independent if and only if P(A ∩ B) = P(A) P(B).

Comments