Square Root of 15

In Mathematics, the square root of 15 is a number that when multiplied by itself yields the original number 15. Because it cannot be stated in the form of p/q, the square root of 15 is an irrational number. In this post, we’ll go through two distinct ways for finding the square root of 15 in detail such as the long division method and the prime factorization method.

Table of Contents:

• What is the Value of Square Root of 15?
• Radical Form of Square Root of 15
• Prime Factorization Method for the Square Root of 15
• Long Division Method to Find Square Root of 15
• Examples
• FAQs

What is the Value of Square Root of 15?

The square of 15 is a number if it is multiplied by itself and gives the result as 15. The square root of 15 is symbolically expressed as √15.

Hence, √15 = √(Value × Value)

As a result, multiplying 3.8729 twice yields the original value of 15.

It means √15 = √(3.8729× 3.8729)

√15 = √(3.8729)²

When we take away the square and square root, we get

√15 = ± 3.8729.

Square Root of 15 in Radical Form

The radical version of the square root of 15 can also be used. We can write the simplest radical form of the square root of 15 if we know the prime factorization of 15. As a result, 15’s prime factorization is 3× 5. If it is written in radical form, it is √3×√ 5 (which isn’t the most basic radical form). As a result, √15 is the radical form of the square root of 15.

Square Root of 15 by Prime Factorization Method

To use the prime factorization method to find the √15, first write the prime factorization of 15. Thus, the prime factorization of 15 is 3 × 5.

Thus, √15 = (√3). (√5)

We know that,

√3 = 1.73205

√5 = 2. 23606

Substitute the values of √2 and √5 in the equation above, we get

√15 = 1.732 × 2.236

√15 =3.8729 (approximately)

Square Root of 15 by Long Division Method

The following is the approach for finding the √15 using the long division method:

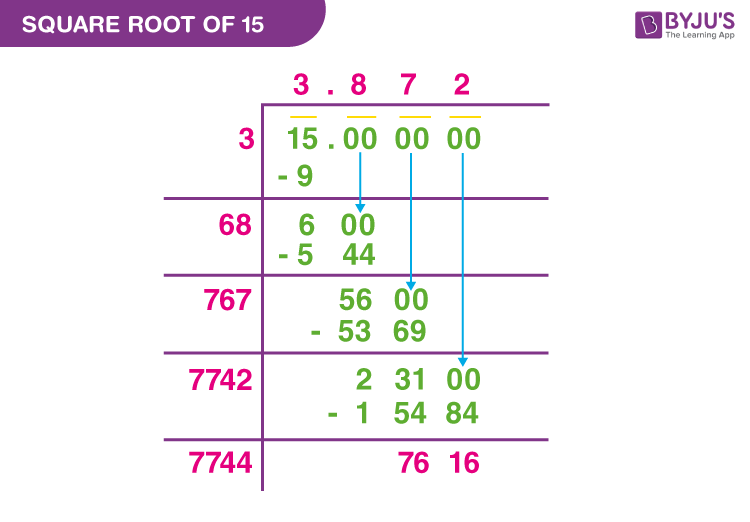
Step 1: First, write the number 15 in decimal form. Add 6 zeros after the decimal point to get the exact value of the √15. As a result, 15 is 15.000000 in decimal form. Now, by placing the bar on top of the number 15, couple it from right to left.

Step 2: Next, divide 15 by a number such that the product of the two same numbers is less than or equal to 15. As a result, 3×3=9, a number less than 15. As a result, we have a quotient of 3 and a remainder of 6.

Step 3: Multiply the quotient value by two, and we get six. Now, use 60 as the new divisor. Bring down the value 00 for the division operation. As a result, the new dividend is 600. Find a number so that (60 + new number) × new number equals the product value, which must be less than or equal to 600. As a result, (60+8) × 8 = 544, which is lower than 600.

Step 4: Subtracting 544 from 600 yields 56 as the new reminder and 38 as the quotient.

Step 5: Take the new quotient 38 and multiply it by two. As a result, we get 76 and infer that our new divisor is 760. Again bringing down two zeros, we now get a new dividend of 5600.

Step 6: Determine a number so that (760 + new number)× new number equals the product value, which must be less than or equal to 5600. As a result, (760+7)× 7 = 5369, a number smaller than 5600.

Step 7: Subtract 5369 from 5600, and the new remainder is 231

Step 8: Repeat the steps until the estimated value of the √15 is obtained to three decimal places. (After bringing down all the values in the dividend, keep the decimal point in the quotient value.)

Step 9: As a result, the square root of 15 is approximately 3.8729.

Video Lessons on Square Roots

Visualising square roots

Finding Square roots

Examples

Example 1:

Reduce the expression: 12 +√15.

Solution:

Given: 12 +√15.

We know that the √15 is 3.8729

Now, substitute the value in the expression, we get:

12 +√15 = 12 + 3.8729

12 +√15 = 15.8729

Therefore, 12 +√15 is 15.8729.

Example 2:

Simplify the expression: 3√15× 4√15.

Solution:

Given: 3√15× 4√15

3√15× 4√15 = (3×4)(√15)²

3√15× 4√15 = 12×15 = 180

Hence, the simplified form of 3√15× 4√15 is180.

Example 3:

Calculate the value of k, if 2k+ √15 = 42.

Solution:

Given equation: 2k+ √15 = 42…(1)

We know that √15 = 3.8729.

Substitute the value in equation (1), we get

2k+3.8729 = 42

2k = 42 – 3.8729

2k = 38.1271

k = (38.1271)/2

k = 19.06355

Therefore, the value of k is 19.06, which is rounded to two decimal places.