Representation Of Decimals On Number Line

Decimals are used in situations where more precision is required in comparison to the whole numbers. For example, when we have to divide 3 apples among 4 kids, we cannot use whole numbers to denote the result of the division, as the fraction of share that is 0.75 lies between 0 and 1. In order to deal with similar other systems, the concept of decimal was introduced.

What are Decimal Numbers?

A decimal number is a number where the integer part is separated from the fractional part with the help of a decimal point. The digits are placed to the left and to the right of the decimal to represent numbers greater than or less than one.

There are certain rules to be followed while reading a decimal number. For e.g. 1.23 is read as one point two three and not one point twenty-three.

What is Decimal Representation?

In Number system, each and every real number can be represented in the form of a decimal. The decimal representation of any non-negative real numbers “r” is an expression which is in the form of series and is traditionally written as:

where a_i is a non-negative integer

a₁, a₂, …are the integers satisfying the condition 0≤ a_i≤ 9

For example, if we take the rational number 1/2, it can also be written as 0.5. In the given example,

“0” represents the whole number part

“.” represents a decimal point

“5” represents the decimal part.

For any rational number which is the ratio of any two numbers, can have either a terminating decimal representation or a repeating representation. Similarly, for any fraction of number, we can represent the number using the decimal value. Some of the examples of the recurring decimal representations are as follows:

1/3 = 0.33333..

1/7 =  0.142857142857…

In order to understand the concept of decimals, let us make a square table with 1 row and 10 columns, as shown in the figure.

Let us fill four of these blocks, as shown below

The fraction of colored blocks to the total blocks can be written as 4/10. Another representation for the same can be given in terms of decimals, like 0.4. Here 0.4 = 4 * or can be written as 4 tenths.

Similarly, if we take a square of 10 rows and 10 columns, we get 100 small squares. If we colour 27 of these blocks, the fractional representation can be written as 27/100.

Here 27/100 = 27*1/100 = 27 hundredth which is represented in the decimal form as 0.27.

So when we have a number 2.34, it is equivalent to 2 + 3 tenths and 4 hundredths.

How to Represent the Decimals on the Number Line?

We know how to represent whole numbers on the number line. Let us consider the image shown below. Here, the digits 0 and 1 are represented on the number line.

If we divide the number line into two equal parts, as shown in the figure below, what value does mid-point hold? We will say half of what the graduation between 0 and 1 holds.

So, the point represents (1-0)/2 = 0.5

In order to represent decimals on the number line, we divide the section between two whole numbers as per the places after decimal present in the number to be represented.

Decimal Representation on Number Line Examples

Example 1:

Represent 0.8 on the number line.

Solution:

As we know, the number 0.8 is equivalent to 8 tenths, so we divide the section between 0 and 1 into 10 equal parts. Now, stepping 8 points from 0 towards 1 gives us 0.8.

Example 2:

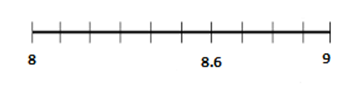
Represent 8.6 on the number line.

Solution:

The number 8.6 = 8 + 0.6

We start from the number 8 on the number line and divide the section between 8 and 9 into 10 equal parts. Now, taking 6 steps from 8 towards 9 gives us the representation of 8.6

To solve more problems on the topic like the square root of decimals, you can visit us www.byjus.com also, download BYJU’S – The Learning App to learn Maths with ease.