MSBSHSE Solutions For SSC (Class 10) Maths Part 2 Chapter 6 - Trigonometry

MSBSHSE Solutions For SSC (Class 10) Maths Part 2 Chapter 6 – Trigonometry gives detailed explanations to each and every solution. These solutions help the students to familiarize themselves with the concepts of Trigonometry. BYJU’S gives 100% perfect solutions designed by our expert team. Students can easily download the solutions in PDF format for free. This chapter deals with Trigonometric ratios and Trigonometric identities. Angle of Elevation and Angle of Depression is discussed in this chapter. Various problems on Applications of trigonometry are solved using Trigonometric identities are solved in this chapter of Maharashtra State Board Class 10 Solutions.

Download the PDF of Maharashtra Solutions For SSC Maths Part 2 Chapter 6 Trigonometry

Access answers to Maths MSBSHSE Solutions For SSC Part 2 Chapter 6 – Trigonometry

Practice set 6.1 Page 131

1. If sin = 7/25 , find the values of cos and tan.

Solution:

Given sin = 7/25

We have sin²+cos² = 1

(7/25)²+ cos² = 1

(49/625)+ cos² = 1

cos² = 1-(49/625)

cos² = (625-49)/625

cos² = 576/625

Taking square root on both sides

cos = 24/25

tan = sin/cos

= (7/25) ÷(24/25)

= (7/25) ×(25/24)

= 7/24

Hence cos = 24/25 and tan = 7/24.

2. If tan = 3/4 , find the values of sec and cos.

Solution:

Given tan = 3/4

We have 1+tan²= sec²

1+(3/4)² = sec²

1+(9/16) = sec²

sec² = (16+9)/16 = 25/16

Taking square root on both sides

sec = 5/4

We have cos = 1/sec

cos = 1÷(5/4)

cos = 4/5

Hence sec = 5/4 and cos = 4/5.

3. If cot = 40/9 , find the values of cosec and sin.

Solution:

Given cot = 40/9

We have 1+cot² = cosec²

1+(40/9)² = cosec²

1+(1600/81) = cosec²

(81+1600)/81 = cosec²

1681/81 = cosec²

cosec² = 1681/81

Taking square root on both sides

cosec = 41/9

We have sin = 1/cosec

sin = 1÷(41/9)

sin = 9/41

Hence cosec = 41/9 and sin = 9/41.

4. If 5sec- 12cosec = 0, find the values of sec, cos and sin.

Solution:

Given 5sec- 12cosec = 0

5sec = 12cosec

5/cos = 12/sin [sec = 1/cos and cosec = 1/sin]

5/12 = cos/sin

sin/cos = 12/5

tan = 12/5

We know that 1+tan² = sec²

1+(12/5)² = sec²

1+(144/25) = sec²

(25+144)/25 = sec²

169/25 = sec²

Taking square root on both sides

sec = 13/5

cos = 1/sec = 5/13

We know that sin²+cos²=1

sin²+(5/13)² = 1

sin² = 1-(5/13)²

sin² = 1-(25/169)

sin² = (169-25)/169

sin² = 144/169

Taking square root on both sides

sin = 12/13

Hence sec = 13/5 , cos = 5/13 and sin = 12/13.

5. If tan = 1 then, find the values of (sin+ cos)/( sec+ cosecθ ).

Solution:

Given tan = 1

We know that tan 45˚ = 1

= 45˚

sin 45 = 1/√2

cos45 = 1/√2

sec45 = √2

cosec45 = √2

(sin+ cos)/( sec+ cosecθ ) = (sin45+ cos45)/( sec45+ cosec45 )

= [(1/√2)+( 1/√2)]÷[√2+√2]

= (2/√2)÷2√2

= (2/√2)×(1/2√2)

= 1/2

Hence (sin+ cos)/( sec+ cosecθ ) = 1/2

6. Prove that:

(1) sin²/ cos + cos = sec

(2) cos² (1 + tan² ) = 1

(3) √[(1-sin)/(1+ sin)] = sec – tan

(4) ( sec – cos)( cot + tan) = tan sec

(5) cot + tan = cosec sec

(6) 1/(secθ-tanθ) = sec + tan

Solution:

(1) sin²/ cos + cos = (sin²+cos²)/cos

= 1/cos [sin²+cos² = 1]

= sec [1/cos = sec]

Hence proved.

(2) cos² (1 + tan² ) = cos² +sin² [cos² ×tan² = cos² ×sin²/cos² = sin²]

= 1 [sin²+cos² = 1]

Hence proved.

(3) √[(1-sin)/(1+ sin)] = √[(1-sin)/(1+ sin)]×√[(1- sin)/(1- sin)] [rationalizing denominator]

= √[(1-sin)²/(1-sin²)]

= √[(1-sin)²/cos² [1-sin² = cos² ]

= (1-sin)/cos [taking square root]

= (1/cos)-(sin/cos)

= sec-tan [1/cos = sec , sin/cos = tan

Hence proved.

(4) ( sec – cos)( cot + tan) = LHS

∵sec = 1/cos , cot = cos/sin , tan = sin/cos

LHS = (1/cos)-cos][(cos/sin)+(sin/cos)]

LHS = [(1-cos²)/cos][( cos²+sin²)/(soncos)]

= [sin²/cos][1/sincos] [∵1-cos² = sin²]

= sin/cos²

= sectan [sin/cos = tan, 1/cos =sec]

= RHS

Hence proved.

(5) cot + tan = (cos/sin) +(sin/cos) [∵cot = cos/sin , tan = sin/cos]

= (cos²+ sin²)/sincos

= 1/ sincos [∵cos²+ sin²= 1]

= cosecsec [1/ sin = cosec , 1/cos = sec]

Hence proved.

(6) 1/(secθ-tanθ) = 1/(secθ-tanθ) × (sec + tan)/(sec+tan) [rationalising denominator]

= (sec+tan)/( sec²-tan²)

= sec+tan [∵sec²-tan² = 1]

Hence proved.

Practice Set 6.2 Page 137

1. A person is standing at a distance of 80m from a church looking at its top. The angle of elevation is of 45°. Find the height of the church.

Solution:

Let C represent position of person and AB represent height of the church.

Angle of elevation = C = 45˚

BC = 80m

In right angled triangle ABC , tan = tan 45˚ = AB/BC

1 = AB/80

AB = 80

Hence height of the church is 80m.

2. From the top of a lighthouse, an observer looking at a ship makes angle of depression of 60°. If the height of the lighthouse is 90 metre, then find how far the ship is from the lighthouse. (√3 =1.73)

Solution:

Let C represent position of ship and AB represent height of the light house

Given AB = 90m

Angle of depression DAC = 60˚

Here BCAD.

BCA = DAC [Alternate interior angles]

BCA = 60˚

In ABC tan60 = AB/BC

√3 = 90/BC

BC = 90/√3 = 90√3/3

= 30√3

= 30 ×1.73

= 51.9

Hence the ship is 51.9 m away from light house.

3. Two buildings are facing each other on a road of width 12 metre. From the top of the first building, which is 10 metre high, the angle of elevation of the top of the second is found to be 60°. What is the height of the second building?

Solution:

Let AB represent height of first building and CD represent height of second building.

BD is the width of the road.

Draw AMCD

Given Angle of elevation CAM = 60˚

Given AB = 10

BD = 12

In AMDB , D = B = 90˚

Since AMCD , M = 90˚

A = 90˚ [Angle sum property of quadrilateral]

Since each angle equal to 90 ˚ AMDB is a rectangle.

Opposite sides are equal.

AB =MD = 10

AM = BD = 12

InAMC, tan 60˚ = CM/AM

√3 = CM/12

CM = 12√3 = 20.76

CD = CM+DM

CD = 20.76 +10 = 30.76

Hence height of second building is 30.76m.

Problem Set 6 Page 138

1. Choose the correct alternative answer for the following questions.

(1) sin cosec = ?

(A) 1 (B) 0 (C) 1/2 (D) √2

Solution:

sin = 1/cosec

sin cosec =(1/cosec)×cosec = 1

Hence option A is the answer.

(2) cosec45° =?

(A) 1/√2 (B) √2 (C) √3/2 (D) 2/√3

Solution:

cosec45 = √2

Hence option B is the answer.

(3) 1 + tan² = ?

(A) cot² (B) cosec² (C) sec² (D) tan²

Solution:

1 + tan² = sec²

Hence option C is the answer.

(4) When we see at a higher level , from the horizontal line,angle formed is……. .

(A) angle of elevation. (B) angle of depression. (C) 0 (D) straight angle.

Solution:

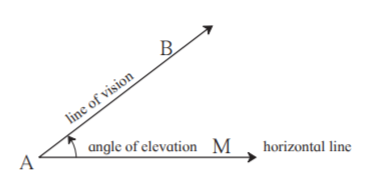
When we see at a higher level , from the horizontal line,angle formed is angle of elevation.

Hence option A is the answer.

2. If sin = 11/61, find the values of cos using trigonometric identity.

Solution:

Given sin = 11/61

Sin²+cos² = 1 [Trigonometric identity]

(11/61)²+cos² = 1

cos² = 1-(11/61)²

= 1-121/3721

= (3721-121)/3721

= 3600/3721

Taking square root on both sides

cos = 60/61

Hence the value of cos = 60/61.

3. If tan = 2, find the values of other trigonometric ratios.

Solution:

Given tan = 2

We have 1+tan² = sec²

1+2² = sec²

sec² = 5

Taking square root on both sides

sec =√5

cos = 1/sec = 1/√5

tan = sin/cos

2 = sin÷(1/√5)

sin = 2/√5

cosec = 1/sin

coesc = √5/2

cot= 1/tan

cot = 1/2

Hence sin = 2/√5, cosec = √5/2, cos = 1/√5, sec = √5 and cot = 1/2

4. If sec = 13/12 , find the values of other trigonometric ratios

Solution:

Given sec = 13/12

cos = 1/sec = 12/13

We have 1+tan² = sec²

1+ tan² = (13/12)²

tan² = (13/12)²-1 = (169/144)-1 = (169-144)/144 = 25/144

Taking square root on both sides

tan = 5/12

cot = 1/tan = 12/5

sin/cos = tan

sin = tan×cos

sin = (5/12)×(12/13)

sin = 5/13

cosec = 1/sin = 13/5

Hence cos = 12/13 , tan = 5/12, cot = 12/5 , sin = 5/13 and cosec = 13/5

5. Prove the following.

(1) sec(1 – sin) (sec + tan) = 1

(2) (sec + tan) (1 – sin) = cos

(3) sec² + cosec² = sec²× cosec²

(4) cot² – tan² = cosec² – sec²

(5) tan⁴ + tan² = sec⁴ – sec²

(6)[ 1/(1- sin θ)]+[1/(1+ sinθ)] = 2 sec²

Solution:

(1) sec(1 – sin) (sec + tan) = (sec-secsin)(sec + tan)

= (sec-tan)(sec+tan) [secsin = sin/cos = tan]

= sec²-tan²

= 1 [1+tan² = sec²]

Hence proved.

(2) (sec + tan) (1 – sin) = [(1/cos)+(sin/cos)](1 – sin)

= [(1+sin)/cos]×(1-sin)

= (1-sin²)/cos

= cos²/cos

= cos

Hence proved.

(3) sec² + cosec² = (1/cos²) +(1/sin²)

= (sin²+cos²)/sin² cos²

= 1/ sin² cos² [sin²+cos² = 1]

= sec²× cosec²

Hence proved.

(4) cot² – tan² = (cosec²-1)-(sec²-1) [∵cot² = cosec²-1 and tan² = sec²-1]

= cosec²-1-sec²+1

= cosec²-sec²

Hence proved.

(5) tan⁴ + tan² = tan²( tan² +1)

= tan²sec² [∵tan² +1= sec²]

= (sec²-1) sec² [∵tan² = sec²-1]

= sec⁴– sec²

Hence proved.

(6)[ 1/(1- sin θ)]+[1/(1+ sinθ)] = [(1+ sinθ)+ (1-sinθ)]/ (1+ sinθ)×(1-sinθ)

= [1+ sinθ+ 1-sinθ]/ (1- sin²θ)

= 2/cos² [1- sin²θ = cos²]

= 2sec² [∵1/ cos² = sec²]

Hence proved.

Trigonometry is a branch of Mathematics that deals with the relationship between side lengths and angles of triangles. This chapter comprises Trigonometric identities and problems based on heights and distances. Sin,cos and tan are the three main trigonometric functions. These solutions help the students to make their learning easy. Get thorough with the mathematical concepts Trigonometry and various problems with BYJU’S.