MSBSHSE Solutions For Class 8 Maths Part 2 Chapter 10 Division of Polynomials

MSBSHSE Solutions For Class 8 Maths Part 2 Chapter 10 Division of Polynomials can be accessed by the students here. This chapter mainly deals with the division of a polynomial by different kinds of polynomials. Mathematics is one of the highest scoring subjects and students are encouraged to use it to their advantage. But, when it comes to exams and preparations, students face a struggle to solve problems on their own. Thus, we at BYJU’S have created Maharashtra State Board Class 8 Part 2 solutions by our subject experts in order to help students prepare for their exams effortlessly. All the solutions are in accordance with the latest Maharashtra Board guidelines to help students secure high marks. Students referring to these solutions will learn the tricks and easy methods to solve problems. The solutions PDF of Maharashtra Board Solutions for Class 8 Maths Chapter 10 Division of Polynomials is given in the link below.

Download the PDF of Maharashtra Board Solutions For Class 8 Maths Part 2 Chapter 10 Division of Polynomials.

Access answers to Maharashtra Board Solutions For Class 8 Maths Part 2 Chapter 10 Division of Polynomials.

Practice Set 10.1 Page No: 64

1. Divide. Write the quotient and the remainder.

(1) 21m² ÷ 7m

Solution:

Thus, quotient = 3m and remainder = 0.

(2) 40a³ ÷ (-10a)

Solution:

Thus, quotient = -4a² and remainder = 0.

(3) (- 48p⁴) ÷ (- 9p²)
Solution:

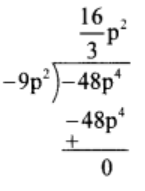
Thus, quotient = 16/3 p² and remainder = 0.

(4) 40m⁵ ÷ 30m³
Solution:

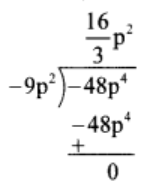
Thus, quotient = 16/3 p² and remainder = 0.

(5) (5x³ – 3x²) ÷ x²
Solution:

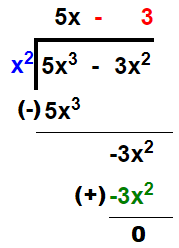
Thus, quotient = 5x – 3 and remainder = 0.

(6) (8p³ – 4p²) ÷ 2p²
Solution:

Thus, quotient = 4p – 2 and remainder = 0.

(7) (2y³ + 4y² + 3) ÷ 2y²
Solution:

Thus, quotient = y + 2 and remainder = 3.

(8) (21x⁴ – 14x² + 7x) ÷ 7x³
Solution:

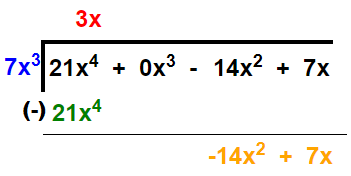
Thus, quotient = 3x and remainder = -14x² + 7x.

(9) (6x⁵ – 4x⁴ + 8x³ + 2x²) ÷ 2x²
Solution:

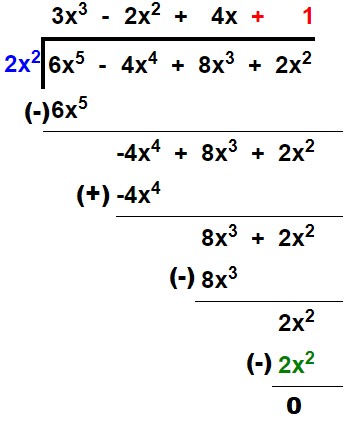
Thus, quotient = 3x³ – 2x² + 4x + 1 and remainder = 0.

(10) (25m⁴ – 15m³ + 10m + 8) ÷ 5m³

Solution:

Thus, quotient = 5m – 3 and remainder = 10m + 8.

Practice Set 10.2 Page No: 66

1. Divide and write the quotient and the remainder.

(1) (y² + 10y + 24) ÷ (y + 4)

Solution:

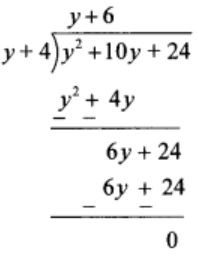
Thus, quotient = y + 6 and remainder = 0

(2) (p² + 7p – 5) ÷ (p + 3)

Solution:

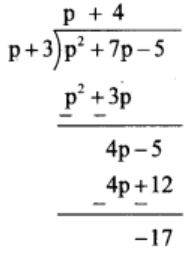
Thus, quotient = p + 4 and remainder = -17

(3) (3x + 2x² + 4x³) ÷ (x – 4)

Solution:

Writing the dividend in descending order of their indices, we have

3x + 2x² + 4x³ = 4x³ + 2x² + 3x

Thus, quotient = 4x² + 18x + 75 and remainder = 300

(4) (2m³ + m² + m + 9) ÷ (2m – 1)

Solution:

Thus, quotient = m² + m + 1 and remainder = 10

(5) (3x – 3x² – 12 + x⁴ + x³) ÷ (2 + x²)

Solution:

Writing the dividend in descending order of their indices, we have

(x⁴ + x³ – 3x² + 3x – 12) ÷ (x² + 2)

Thus, quotient = x² + x – 5 and remainder = x – 2.

(6) (a⁴ – a³ + a² – a + 1) ÷ (a³ – 2)

Solution:

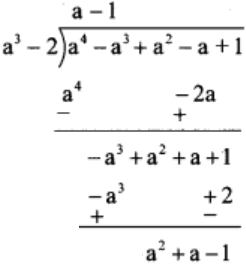
Thus, quotient = a – 1 and remainder = a² + a – 1.

(7) (4x⁴ – 5x³ – 7x + 1) ÷ (4x – 1)

Solution:

Writing the dividend in descending order of their indices, we have

(4x⁴ – 5x³ – 7x + 1) = (4x⁴ – 5x³ + 0x² – 7x + 1)

Thus, quotient = x³ – x² – x/4 – 29/16 and remainder = -13/16.

Further, our experts have solved the difficult problems by using simple steps, so that students of all levels can understand them. The following chapter is about Division of Polynomials, where one will understand how to divide a given polynomial by a monomial and binomial. Regular revision of these concepts over time can strengthen one’s knowledge over the chapter. Students can refer to all other solutions to yield good results in the examination.