MSBSHSE Solutions For Class 9 Maths Part 1 Chapter 5 Linear Equations in Two Variables

MSBSHSE Solutions For Class 9 Maths Part 1 Chapter 5 – Linear Equations in Two Variables are given here with step by step explanations of each and every solution. Here, we provide you error free solutions, which are prepared by our specialized professionals. These solutions help students not only to strengthen their foundation in the subject, but also to crack different types of problems easily. This chapter of Maharashtra Solutions for Class 9 mainly focuses on the concept of Linear Equations in Two Variables and solving simultaneous linear equations. Let us have a look at some of the important concepts that are discussed in this chapter.

• Elimination method of solving simultaneous equations
• General form of linear equation
• Substitution method of solving simultaneous equations
• Word problems based on simultaneous equations

Download the PDF of Maharashtra Solutions For Class 9 Maths Part 1 Chapter 5 Linear Equations in Two Variables

Access answers to Maths MSBSHSE Solutions For Class 9 Part 1 Chapter 5 – Linear Equations in Two Variables

Practice set 5.1 Page no: 86

1. By using variables x and y form any five linear equations in two variables.

Solution:

The general form of a linear equation in two variables x and y is ax + by + c = 0,

where a, b, c are real numbers and a ≠ 0, b ≠ 0.

Five linear equations in two variables are as follows:

i. 3x + 4y – 12 = 0

ii. 3x – 4y + 12 = 0

iii. 5x + 5y – 6 = 0

iv. 7x + 12y – 11 = 0

v. x – y + 5 = 0

2. Write five solutions of the equation x + y = 1.

Solution:

(a) Let x = 1,

As, x + y = 7

⇒ 1 + y = 7

⇒ y = 6

Hence, solution is x = 1 and y = 6.

(b) Let x = 2,

As, x + y = 7

⇒ 2 + y = 7

⇒ y = 5

Hence, solution is x = 2 and y = 5.

(c) Let x = 3,

As, x + y = 7

⇒ 3 + y = 7

⇒ y = 4

Hence, solution is x = 3 and y = 4.

(d) Let x = 4,

As, x + y = 7

⇒ 4 + y = 7

⇒ y = 3

Hence, solution is x = 4 and y = 3.

(e) Let x = 5,

As, x + y = 7

⇒ 5 + y = 7

⇒ y = 2

Hence, solution is x = 5 and y = 2.

3. Solve the following sets of simultaneous equations.
i. x + y = 4; 2x – 5y = 1
ii. 2x + y = 5; 3x – y = 5
iii. 3x – 5y = 16; x – 3y= 8
iv. 2y – x = 0; 10x + 15y = 105
v. 2x + 3y + 4 = 0; x – 5y = 11
vi. 2x – 7y = 7; 3x + y = 22

Solution:

i. x + y = 4

∴ x = 4 – y …(i)

2x – 5y = 1 ……(ii)

Substituting x = 4 – y in equation (ii),

2(4 – y) – 5y = 1

∴ 8 – 2y – 5y = 1

∴ 8 – 7y = 1

8 – 1 = 7y

7 = 7y

y = 7/7

∴ y = 1

Substituting y = 1 in equation (i),

x = 4 – 1 = 3

∴ (3,1) is the solution of the given equations.

ii. 2x + y = 5 …(i)

3x – y = 5 …(ii)

Adding equations (i) and (ii),

2x + y = 5

+ 3x – y = 5

5x = 10

∴ x = 10/5

∴ x = 2

Substituting x = 2 in equation (i),

2(2) + y = 5

4 + y = 5

∴ y = 5 – 4 = 1

∴ (2, 1) is the solution of the given equations.

iii. 3x – 5y = 16 …(i)

x – 3y = 8

∴x = 8 + 3y …..(ii)

Substituting x = 8 + 3y in equation (i),

3(8 + 3y) – 5y = 16

24 + 9y- 5y = 16

∴4y= 16 – 24

∴ 4y = -8

∴ y = −8/4

y = -2

Substituting y = -2 in equation (ii),

x = 8 + 3 (-2)

∴ x = 8 – 6 = 2

∴ (2, -2) is the solution of the given equations.

iv. 2y – x = 0

∴ x = 2y …(i)

10x + 15y = 105 …(ii)

Substituting x = 2y in equation (ii),

10(2y) + 15y = 105

∴ 20y + 15y = 105

∴ 35y = 105

∴ y = 105/35

∴ y = 3

Substituting y = 3 in equation (i),

x = 2y

∴ x = 2(3) = 6

∴ (6, 3) is the solution of the given equations.

v. 2x + 3y + 4 = 0 …(i)

x – 5y = 11

∴x = 11 + 5y …(ii)

Substituting x = 11 + 5y in equation (i),

2(11 +5y) + 3y + 4 = 0

∴ 22 + 10y + 3y + 4 = 0

∴ 13y + 26 = 0

∴ 13y = -26

∴y = −26/13

∴ y = -2

Substituting y = -2 in equation (ii),

x = 11 + 5y

∴ x = 11 + 5(-2)

∴ x = 11 – 10 = 1

∴ (1, -2) is the solution of the given equations.

vi. 2x – 7y = 7 …(i)

3x + y = 22

∴ y = 22 – 3x ……(ii)

Substituting y = 22 – 3x in equation (i),

2x – 7(22 – 3x) = 7

∴ 2x – 154 + 21x = 7

∴ 23x = 7 + 154

∴ 23x = 161

∴ x = 161/23

∴ x = 7

Substituting x = 7 in equation (ii),

y = 22 – 3x

∴ y = 22 – 3(7)

∴ 7 = 22 -21= 1

∴ (7, 1) is the solution of the given equations.

Practice set 5.2 Page no: 90

1. In an envelope there are some 5 rupee notes and some 10 rupee notes. Total amount of these notes together is 350 rupees. Number of 5 rupee notes are less by 10 than number of 10 rupee notes. Then find the number of 5 rupee and 10 rupee notes.

Solution:

Let the number of ₹5 notes be ‘x’ and the number of ₹10 notes be ‘y’

Total amount of x notes of ₹ 5 = ₹ 5x

Total amount of y notes of ₹ 10 = ₹ 10y

∴ Total amount = 5x + 10y

According to the first condition,

total amount of the notes together is ₹350.

∴ 5x + 10y = 350 …(i)

According to the second condition,

Number of ₹ 5 notes are less by 10 than twice the number of ₹ 10 notes.

∴ x = 2y – 10

∴ x – 2y = -10 …..(ii)

Multiplying equation (ii) by 5,

5x – 10y = -50 …(iii)

Adding equations (i) and (iii),

5x + 10y =350

+ 5x – 10y = -50

10x =300

∴ x = 300/10

∴ x = 30

Substituting x = 30 in equation (ii),

x – 2y = -10

30 – 2y = -10

∴ 30 + 10 = 2y

∴ 40 = 2y

∴ y = 40/2

∴ y = 20

There are 30 notes of ₹ 5 and 20 notes of ₹ 10 in the envelope.

2. The denominator of a fraction is 1 more than twice its numerator. If 1 is added to numerator and denominator respectively, the ratio of numerator to denominator is
1: 2. Find the fraction.

Solution:

Let the numerator of the fraction be ‘x’ and its denominator be ‘y’.

Then, the required fraction is xy.

According to the first condition,

the denominator is 1 less than twice its numerator.

∴ y = 2x – 1

∴ 2x – y = 1 …(i)

According to the second condition,

if 1 is added to the numerator and the denominator, the ratio of numerator to denominator is 3 : 5.

∴ x + 1y + 1 = 3/5

∴ y + 1 = 5

∴ 5(x + 1) = 3(y + 1)

∴ 5x + 5 = 3y + 3

∴ 5x – 3y = 3 – 5

∴ 5x – 3y = -2 ……(ii)

Multiplying equation (i) by 3,

6x – 3y = 3 …(iii)

Subtracting equation (ii) from (iii), we get

x = 5

Substituting x = 5 in equation (i),

∴ 2x – y = 1

∴ 2(5) – y = 1

∴ 10 – y = 1

∴ y= 10 – 1 =9

∴ The required fraction is 5/9.

3. The sum of ages of Priyanka and Deepika is 34 years. Priyanka is elder to Deepika by 6 years. Then find their today’s ages.

Solution:

Let the present age of Priyanka be ‘x’ years and that of Deepika be ‘y’ years.

According to the first condition,

Priyanka’s age + Deepika’s age = 34 years

∴ x + y = 34 …(i)

According to the second condition,

Priyanka is elder to Deepika by 6 years.

∴ x =y + 6

∴ x – y = 6 …..(ii)

Adding equations (i) and (ii),

2x = 40

∴ x = 20

Substituting x = 20 in equation (i),

x + y = 34

∴ 20 + y = 34

∴ y = 34 -20= 14

∴ The present age of Priyanka is 20 years and that of Deepika is 14 years.

4. The total number of lions and peacocks in a certain zoo is 50. The total number of their legs is 140. Then find the number of lions and peacocks in the zoo.

Solution:

Let the number of lions in the zoo be ‘x’ and the number of peacocks be ‘y’.

According to the first condition,

the total number of lions and peacocks is 50.

∴ x + y = 50 …(i)

Lion has 4 legs and Peacock has 2 legs.

According to the second condition,

the total number of their legs is 140.

∴ 4x + 2y = 140

Dividing both sides by 2,

2x + y = 70 …(ii)

Subtracting equation (i) from (ii),

x = 20

Substituting x = 20 in equation (i),

x + y = 50

∴ 20 + y = 50

∴ y = 50 – 20 = 30

∴ The number of lions and peacocks in the zoo are 20 and 30 respectively.

5. Sanjay gets fixed monthly income. Every year there is a certain increment in his salary. After 4 years, his monthly salary was Rs. 4500 and after 10 years his monthly salary became 5400 rupees, then find his original salary and yearly increment.

Solution:

Let the original salary of Sanjay be ₹ ‘x’ and his yearly increment be ₹ ‘y’.

According to the first condition, after 4 years his monthly salary was ₹ 4500

∴ x + 4y = 4500 …..(i)

According to the second condition,

after 10 years his monthly salary became ₹ 5400

∴ x + 10y = 5400 …(ii)

Subtracting equation (i) from (ii),

6y = 900

y = 900/6

∴ y = 150

Substituting y = 150 in equation (i),

x + 4y = 4500

∴ x +4(150) = 4500

∴ x + 600 = 4500

x = 4500 – 600 = 3900

∴ The original salary of Sanjay is ₹ 3900 and his yearly increment is ₹ 150.

6. The price of 3 chairs and 2 tables is 4500 rupees and price of 5 chairs and 3 tables is 7000 rupees, then find the price of 2 chairs and 2 tables.

Solution:

Let the price of one chair be ₹ ‘x’ and that of one table be ₹ ‘y’.

According to the first condition,

the price of 3 chairs and 2 tables is ₹ 4500

∴ 3x + 2y = 4500 ,..(i)

According to the second condition, the price of 5 chairs and 3 tables is ? 7000

∴ 5x + 3y = 7000 …(ii)

Multiplying equation (i) by 3,

9x + 6y = 13500 ….(iii)

Multiplying equation (ii) by 2,

10x + 6y= 14000 …(iv)

Subtracting equation (iii) from (iv),

x = 500

Substituting x = 500 in equation (i),

3x + 2y = 4500

∴ 3(500)+ 2y = 4500

∴ 1500 + 2y = 4500

∴ 2y = 4500- 1500

∴ 2y = 3000

∴ y = 30002

∴ y = 1500

∴ Price of 2 chairs and 2 tables = 2x + 2y

= 2(500)+ 2(1500)

= 1000 + 3000 = ₹ 4000

∴ The price of 2 chairs and 2 tables is ₹ 4000.

7. The sum of the digits in a two-digits number is 9. The number obtained by interchanging the digits exceeds the original number by 27. Find the two-digit number.

Solution:

Let the unit digit be ‘x’

Let the digit at ten’s place be ‘y’

The original number will be 10y + x

Given,

Sum of digits = 9

⇒ x + y = 9

⇒ x = 9 – y ….. (i)

Also,

If the digits are interchanged,

Reversed number will be = 10x + y

As, reversed number exceeds the original number by 27,

⇒ (10x + y) – (10y + x) = 27

⇒ 10x + y – 10y – x = 27

⇒ 9x – 9y = 27

⇒ x – y = 3

Using equation (i)

⇒ 9 – y – y = 3

⇒ -2y = -6

⇒ y = 3

Using this in equation (i)

⇒ x = 9 – 3 = 6

Hence the original number is 10y + x = 10(3) + 6 = 30 + 6 = 36.

8. In ΔABC, the measure of angle A is equal to the sum of the measures of ∠B and ∠C. Also, the ratio of measures of ∠B and ∠C is 4: 5. Then find the measures of angles of the triangle.

Solution:

Given that, In ΔABC

∠A = ∠B + ∠C …… (i)

Let ∠B = x and ∠C = y

Then,

∠A = x + y

In ΔABC, By angle sum property of triangle

∠A + ∠B + ∠C = 180°

⇒ x + y + x + y = 180

⇒ 2x + 2y = 180

⇒ x + y = 90

⇒ x = 90 – y ….. (ii)

Also, Given that

∠B/ ∠C = 4/5

⇒ x/y = 4/5

⇒ 5x = 4y

From equation (ii)

⇒ 5(90 – y) = 4y

⇒ 450 – 5y = 4y

⇒ 9y = 450

⇒ y = 50°

Putting this in equation (ii)

⇒ x = 90 – 50 = 40°

Therefore, we have

∠A = x + y = 40° + 50° = 90°

∠B = x = 40°

∠C = y = 50°

9. Divide a rope of length 560 cm into 2 parts such that twice the length of the smaller part is equal to 1/3 of the larger part. Then find the length of the larger part.

Solution:

Let the length of the smaller part of the rope be ‘x’ cm and that of the larger part be ‘y’ cm.

According to the first condition,

total length of the rope is 560 cm.

∴ x + y = 560 …(i)

Twice the length of the smaller part = 2x

1/3rd length of the larger part = 1/3y

According to the second condition,

2x = 1/3 × 3

∴ 6x = y

∴ 6x – y = 0 ……(ii)

Adding equations (i) and (ii),

x = 560/7

∴ x = 80

Substituting x = 80 in equation (ii),

6x – y = 0

∴ 6(80) – y = 0

∴ 480 – y = 0

∴ y = 480

∴ The length of the larger part of the rope is 480 cm.

10. In a competitive examination, there were 60 questions. The correct answer would carry 2 marks, and for incorrect answer 1 mark would be subtracted. Yashwant had attempted all the questions and he got total 90 marks. Then how many questions he got wrong?

Solution:

Let us suppose that Yashwant got ‘x’ questions right and ‘y’ questions wrong.

According to the first condition, total number of questions in the examination are 60.

∴ x + y = 60 …(i)

Yashwant got 2 marks for each correct answer and 1 mark was deducted for each wrong answer.

∴ He got 2x – y marks.

According to the second condition,

he got 90 marks.

2x – y = 90 … (ii)

Adding equations (i) and (ii),

3x = 150

x = 150/3

∴ x = 50

Substituting x = 50 in equation (i),

50 + y = 60

∴ y = 60 – 50 = 10

∴ Yashwant got 10 questions wrong.

Problem set 5 Page no: 91

1. Choose the correct alternative answers for the following questions.
i. If 3x + 5y =9 and 5x + 3y =7 then What is the value of x + y?
A. 2
B. 16
C. 9
D. 7

Solution:

A. 2

Explanation:

3x + 5y = 9 …. (i)

5x + 3y = 7 ….. (ii)

Adding i and ii we get

3x + 5y + 5x + 3y = 9 + 7

⇒ 8x + 8y = 16

Dividing both side by 8, we get

⇒ x + y = 2

ii. ‘When 5 is subtracted from length and breadth of the rectangle, the perimeter becomes 26.’ What is the mathematical form of the statement?
A. x – y = 8
B. x + y = 8
C. x + y =23
D. 2x + y = 21

Solution:

C. x + y =23

Explanation:

Let the length be ‘x’ and breadth be ‘y’ units.

Perimeter of triangle = 2(x + y) units

If 5 is subtracted from length and breadth

Perimeter = 26 units

⇒ 2 (x – 5 + y – 5) = 26

⇒ 2(x + y – 10) = 26

⇒ x + y – 10 = 13

⇒ x + y = 23

iii. Ajay is younger than Vijay by 5 years. Sum of their ages is 25 years. What is Ajay’s age?
A. 20
B. 15
C. 10
D. 5

Solution:

B. 15

Explanation:

Let Ajay’s age be ‘x’ years and Vijay’s age be ‘y’ years.

Given, Ajay is younger than Vijay by 5 years

⇒ x = y – 5 …. (i)

Also, Sum of their ages is 25 years,

⇒ x + y = 25

From (i)

⇒ y – 5 + y = 25

⇒ 2y = 30

⇒ y = 15

Putting this in (i)

⇒ x = 15 – 5 = 10

Age of Ajay = x = 10 Years

Age of Vijay = y = 15 Years

2. Solve the following simultaneous equations.
i. 2x + y = 5; 3x – y = 5
ii. x – 2y = -1; 2x – y = 7
iii. x + y = 11; 2x – 3y = 7
iv. 2x + y = -2; 3x – y = 7
v. 2x – y = 5; 3x + 2y = 11
vi. x – 2y = -2; x + 2y = 10

Solution:

i. 2x + y = 5 …(i)

3x – y = 5 …(ii)

Adding equations (i) and (ii),

2x + y = 5

+ 3x – y = 5

5x = 10

∴ x = 10/5

∴ x = 2

Substituting x = 2 in equation (i),

2(2) + y = 5

4 + y = 5

∴ y = 5 – 4 = 1

∴ (2, 1) is the solution of the given equations.

ii. x – 2y = -1

∴x = 2y – 1 … .(i)

∴ 2x – y = 7 ….(ii)

Substituting x = 2y – 1 in equation (ii),

2(2y – 1) – y = 7

∴ 4y – 2 – y = 7

∴ 3y = 7 + 2

∴ 3y = 9

∴ y = 9/3

∴ y = 3

Substituting y = 3 in equation (i),

x = 2y – 1

∴ x = 2(3) – 1

∴ x = 6 – 1 = 5

∴ (5, 3) is the solution of the given equations.

iii. x + y = 11

∴ x = 11 – y …(i)

2x – 3y = 7 …….(ii)

Substituting x = 11 -y in equation (ii),

2(11 – y) – 3y = 7

∴ 22 – 2y – 3y = 1

∴ 22 – 5y = 7

∴ 22 – 7 = 5y

∴ 15 = 5y

∴ y = \(\frac { 15 }{ 5 }\)

∴ y = 3

Substituting y = 3 in equation (i),

x = 11 – y

∴ x = 11 – 3 = 8

∴ (8, 3) is the solution of the given equations.

iv. 2x + y = -2 …(i)

3x – y = 7 …(ii)

Adding equations (i) and (ii),

2x + y = -2

+ 3x – y = l

5x = 5

∴ x = \(\frac { 5 }{ 5 }\)

∴ x = 1

Substituting x = 1 in equation (i),

2x + y = -2

∴ 2(1) +y = -2

2 + y = -2

∴ y = – 2 – 2

∴ y = -4

∴ (1, -4) is the solution of the given equations.

v. 2x – y = 5

∴ -y = 5 – 2x

∴ y = 2x – 5 …(i)

3x + 2y = 11 ……(ii)

Substituting y = 2x – 5 in equation (ii),

3x + 2(2x – 5) = 11

∴ 3x + 4x- 10= 11

∴ 7x = 11 + 10

∴ 7x = 21

∴ x = \(\frac { 21 }{ 7 }\)

∴ x = 3

Substituting x = 3 in equation (i),

y = 2x – 5

∴ y = 2(3) – 5

∴ y = 6 – 5 = 1

∴(3,1) is the solution of the given equations.

vi. x – 2y = -2

∴ x = 2y – 2 …(i)

x + 2y = 10 …..(ii)

Substituting x = 2y – 2 in equation (ii),

2y – 2 + 2y = 10

∴ 4y = 10 + 2

∴ 4y= 12

∴ y = \(\frac { 12 }{ 7 }\)

∴ y = 3

Substituting y = 3 in equation (i),

x = 2y – 2

∴ x = 2(3) – 2

∴ x = 6 – 2 = 4

∴ (4, 3) is the solution of the given equations.

3. By equating coefficients of variables, solve the following equations. [3 Marks each] i. 3x – 4y = 7; 5x + 2y = 3
ii. 5x + 7y= 17; 3x – 2y = 4
iii. x – 2y = -10; 3x – 3y = -12
iv. 4x+y = 34; x + 4y = 16

Solution:

i. 3x – 4y = 7 …(i)

5x + 2y = 3 ….(ii)

Multiplying equation (ii) by 2,

10x + 4y = 6 …(iii)

Adding equations (i) and (iii),

13 x = 13

x = 13/13

∴ x = 1

Substituting x = 1 in equation (i),

3x – 4y = 7

∴ 3(1) – 4y = 7

∴ 3 – 4y = 7

∴ 3 – 7 = 4y

∴ -4 = 4y

∴ y = \(\frac { -4 }{ 4 }\)

∴ y = -1

∴ (1, -1) is the solution of the given equations.

ii. 5x + 7y = 17 …(i)

3x – 2y = 4 …. (ii)

Multiplying equation (i) by 2,

10x + 14y = 34 …(iii)

Multiplying equation (ii) by 7,

21x – 14y = 28 …..(iv)

Adding equations (iii) and (iv),

31 x = 62

x = 62/31

∴ x = 2

Substituting x = 2 in equation (ii),

3x – 2y = 4

∴ 3(2) – 2y = 4

∴ 6 – 2y = 4

∴ 6 – 4 = 2y

∴ 2 = 2y

∴ y = \(\frac { 2 }{ 2 }\)

∴ y = 1

∴ (2,1) is the solution of the given equations.

iii. x – 2y = -10 …. (i)

3x – 5y = -12 ……. (ii)

Multiplying equation (i) by 3,

3x – 6y = -30 …(iii)

Subtracting equation (ii) from (iii),

-y = -18

∴ y = 18

Substituting y = 18 in equation (i),

x – 2y = -10

∴ x – 2(18) = -10

∴ x – 36 = -10

∴ x = -10 + 36 = 26

∴ (26, 18) is the solution of the given equations.

iv. 4x + y = 34 …(i)

x + 4y = 16 …… (ii)

Multiplying equation (i) by 4,

16x + 4y = 136 …(iii)

Subtracting equation (ii) from (iii),

15 x = 120

x = 120/15

x = 8

Substituting x = 8 in equation (i),

4x + y = 34

∴ 4(8) + y = 34

∴ 32 + y = 34

∴ y = 34 – 32 = 2

∴ (8, 2) is the solution of the given equations.

4. Solve the following simultaneous equations.
i.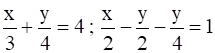
ii.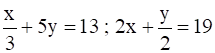 
iii.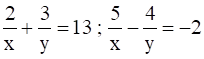 

Solution:

(i) Given

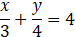
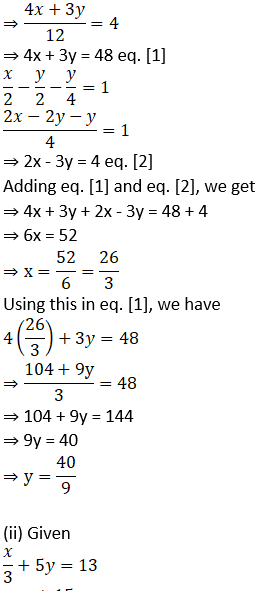
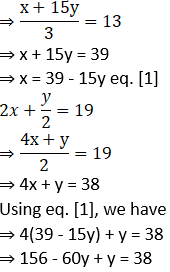
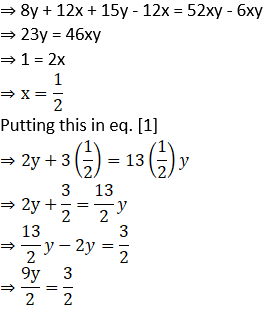
5. A two-digit number is 3 more than 4 times the sum of its digits. If 18 is added to this number, the sum is equal to the number obtained by interchanging the digits. Find the number.

Solution:

Let the unit digit be ‘x’

Let the digit at ten’s place be ‘y’

The original number will be 10y + x

Given, number is 3 more than 4 times the sum of its digits

⇒ 10y + x = 4(x + y) + 3

⇒ 10y + x = 4x + 4y + 3

⇒ 6y – 3x = 3

⇒ 2y – x = 1

⇒ x = 2y – 1 eq. [1]

Also,

If the digits are interchanged,

Reversed number will be = 10x + y

As, reversed number exceeds the original number by 18,

⇒ (10x + y) – (10y + x) = 18

⇒ 10x + y – 10y – x = 18

⇒ 9x – 9y = 18

⇒ x – y = 2

⇒ 2y – 1 – y = 2 eq. [using 1]

⇒ y = 3

Using this in eq. [1]

⇒ x = 2(3) – 1 = 5

Hence the original number is 10y + x = 10(3) + 5 = 30 + 5 = 35.

6. The total cost of 6 books and 7 pens is 79 rupees and the total cost of 7 books and 5 pens is 77 rupees. Find the cost of 1 book and 2 pens.

Solution:

Let the cost of one book be ₹ x and the cost of one pen be ₹ y.

According to the first condition,

the total cost of 8 books and 5 pens is ₹ 420.

∴ 8x + 5y = 420 …(i)

According to the second condition, the total cost of 5 books and 8 pens is ₹ 321.

5x + 8y = 321 ….(ii)

Multiplying equation (i) by 5,

40x + 25y = 2100 …(iii)

Multiplying equation (ii) by 8,

40x + 64y = 2568 … (iv)

Subtracting equation (iii) from (iv),

39 y = 468

y = 468/ 39

∴ y = 12

Substituting y = 12 in equation (i),

8x + 5y = 420

∴ 8x + 5(12) = 420

∴ 8x + 60 = 420

∴ 8x = 420 – 60

∴ 8x = 360

∴ x = \(\frac { 360 }{ 8 }\)

∴ x = 45

Cost of 1 book and 2 pens = x + 2y

= 45 + 2(12)

= 45 + 24

= ₹69

∴ The cost of 1 book and 2 pens is ₹69.

7. The ratio of incomes of two persons is 9: 7. The ratio of their expenses is 4: 3. Every person saves rupees 200, find the income of each.

Solution:

As the ratio of incomes is 9: 7,

Let income of first person = 9x

Income of second person = 7x

Also, ratio of incomes is 4: 3,

Let expenses of first person = 4y

Expenses of second person = 3y

Each person saves 200 Rs,

⇒ 9x – 4y = 200 eq. [1]

⇒ 7x – 3y = 200 eq. [2]

Multiplying eq. [1] by 3 both side and Multiplying eq. [2] by 4 both sides, we get

⇒ 27x – 12y = 600 eq. [3]

⇒ 28x – 12y = 800 eq. [4]

Subtracting eq. [3] from eq. [4], we get

⇒ 28x – 12y – (27x – 12y) = 800 – 600

⇒ 28x – 12y – 27x + 12y = 200

⇒ x = 200

Income of first person = 9x = 9(200) = 1800 Rs

Income of second person = 7x = 7(200) = 1400 Rs

8. If the length of a rectangle is reduced by 5 units and its breadth is increased by 3 units, then the area of the rectangle is reduced by 8 square units. If length is reduced by 3 units and breadth is increased by 2 units, then the area of rectangle will increase by 67 square units. Then find the length and breadth of the rectangle.

Solution:

Let the length of the rectangle be ‘x’ units and the breadth of the rectangle be ‘y’ units.

Area of the rectangle = xy sq. units

length of the rectangle is reduced by 5 units

∴ length = x – 5

breadth of the rectangle is increased by 3 units

∴ breadth = y + 3

area of the rectangle is reduced by 9 square units

∴ area of the rectangle = xy – 9

According to the first condition,

(x – 5)(y + 3) = xy – 9

∴ xy + 3x – 5y – 15 = xy – 9

∴ 3x – 5y = -9 + 15

∴ 3x – 5y = 6 …(i)

length of the rectangle is reduced by 3 units

∴ length = x – 3

breadth of the rectangle is increased by 2 units

∴ breadth = y + 2

area of the rectangle is increased by 67 square units

∴ area of the rectangle = xy + 61

According to the second condition,

(x – 3)(y + 2) = xy + 67

∴ xy + 2x – 3y – 6 = xy + 67

∴ 2x – 3y = 67 + 6

∴ 2x – 3y = 73 …(ii)

Multiplying equation (i) by 3,

9x – 15y = 18 . ..(iii)

Multiplying equation (ii) by 5,

10x – 15y = 365 …(iv)

Subtracting equation (iii) from (iv),

10x- 15y= 365 9x-15y= 18

x = 347

Substituting x = 347 in equation (ii),

2x – 3y = 73

∴ 2(347) – 3y = 73

∴ 694 – 73 = 3y

∴ 621 = 3y

∴ y = 207

∴ The length and breadth of rectangle are 347 units and 207 units respectively.

9. The distance between two places A and B on road is 70 kilometres. A car starts from A and the other from B. If they travel in the same direction, they will meet after 7 hours. If they travel towards each other they will meet after 1 hour, then find their speeds.

Solution:

Let the speed of car at place A is x km/h and that of car at place B is y km/h

If they travel in same direction, they will meet after 7 hours, i.e. the difference of distance covered by them in 7 hours will be equal to distance b/w A and B.

As, distance = speed × time, and distance from A to B is 70 km

⇒ 7x – 7y = 70

⇒ x – y = 10

⇒ x = y + 10 eq. [1]

If they, travel in opposite direction, they will meet after 1 hour i.e. sum of distance travelled by both cars will be equal to the distance b/w A and B.

⇒ x + y = 70

Using eq. [1], we have

⇒ y + 10 + y = 70

⇒ 2y = 60

⇒ y = 30

Using this in eq. [1], we have

x = 30 + 10 = 40

Hence,

Speed of car at A = x = 40 km/h

Speed of car at B = y = 30 km/h

10. The sum of a two-digit number and the number obtained by interchanging its digits is 99. Find the number.

Solution:

Let the unit digit be ‘x’ and digit at ten’s place be ‘y’

Original Number = 10y + x

Number obtained by interchanging digits = 10x + y

Given,

10y + x + 10x + y = 99

⇒ 11x + 11y = 99

⇒ x + y = 9

If x = 1, y = 8 and number is 18

If x = 2, y = 7 and number is 27

If x = 3, y = 6 and number is 36

If x = 4, y = 5 and number is 45

If x = 5, y = 4 and number is 54

If x = 6, y = 3 and number is 63

If x = 7, y = 2 and number is 72

If x = 8, y = 1 and number is 81