MSBSHSE Solutions For Class 9 Maths Part 2 Chapter 1 Basic Concepts In Geometry

MSBSHSE Solutions For Class 9 Maths Part 2 Chapter 1 Basic Concepts In Geometry consists of 100% accurate solutions prepared by our expert team. Each step in the solution is explained to match the student’s understanding. This chapter deals with basic concepts in Geometry such as Point, Line and Plane. The concept of Betweenness is also explained in this chapter. These MSBSHSE Solutions For Class 9 Maths Part 2 Chapter 1 are crucial for students who are preparing for board examinations. These solutions can be downloaded in PDF format.

Download the PDF of Maharashtra Solutions For Class 9 Maths Part 2 Chapter 1 Basic Concepts In Geometry

Access answers to Maths MSBSHSE Solutions For Class 9 Part 2 Chapter 1 – Basic Concepts In Geometry

Practice Set 1.1 Page 5

1. Find the distances with the help of the number line given below.

(i) d(B,E)

(ii) d(J, A)

(iii) d(P, C)

(iv) d(J, H)

(v) d(K, O)

(vi) d(O, E)

(vii) d(P, J)

(viii) d(Q, B)

Solution:

(i)The co-ordinates of B and E are 2 and 5 respectively.

The distance between two points is obtained by subtracting the smaller co-ordinate from the larger co-ordinate.

We know that 52.

Distance between B and E , d(B,E) = 5-2 = 3

Hence d(B,E) = 3.

(ii)The co-ordinates of J and A are -2 and 1 respectively.

The distance between two points is obtained by subtracting the smaller co-ordinate from the larger co-ordinate.

We know that 1-2.

Distance between J and A , d(J,A) = 1-(-2) =1+2 = 3

Hence d(J,A) = 3.

(iii)The co-ordinates of P and C are -4 and 3 respectively.

The distance between two points is obtained by subtracting the smaller co-ordinate from the larger co-ordinate.

We know that 3-4.

Distance between P and C , d(P,C) = 3-(-4) =3+4 = 7

Hence d(P,C) = 7.

(iv) The co-ordinates of J and H are -2 and -1 respectively.

The distance between two points is obtained by subtracting the smaller co-ordinate from the larger co-ordinate.

We know that -1-2.

Distance between J and H , d(J,H) = -1-(-2) = -1+2 = 1

Hence d(J,H) = 1.

(v) The co-ordinates of K and O are -3 and 0 respectively.

The distance between two points is obtained by subtracting the smaller co-ordinate from the larger co-ordinate.

We know that 0-3.

Distance between K and O , d(K,O) = 0-(-3) = 0+3 = 3

Hence d(K,O) = 3.

(vi) The co-ordinates of O and E are 0 and 5 respectively.

The distance between two points is obtained by subtracting the smaller co-ordinate from the larger co-ordinate.

We know that 50.

Distance between O and E , d(O,E) = 5-0 = 5

Hence d(O,E) = 5.

(vii) The co-ordinates of P and J are -4 and -2 respectively.

The distance between two points is obtained by subtracting the smaller co-ordinate from the larger co-ordinate.

We know that -2-4.

Distance between P and J , d(P,J) = -2-(-4) = -2+4 = 2

Hence d(P,J) = 2.

(viii) The co-ordinates of Q and B are -5 and 2 respectively.

The distance between two points is obtained by subtracting the smaller co-ordinate from the larger co-ordinate.

We know that 2-5.

Distance between Q and B , d(Q,B) = 2-(-5) = 2+5 = 7

Hence d(Q,B) = 7.

2. If the co-ordinate of A is x and that of B is y, find d(A, B) .

(i) x = 1, y = 7

(ii) x = 6, y = – 2

(iii) x = – 3, y = 7

(iv) x = – 4, y = – 5

(v) x = – 3, y = – 6

(vi) x = 4, y = – 8

Solution:

(i)Co-ordinate of A = 1

Co-ordinate of B = 7

The distance between two points is obtained by subtracting the smaller co-ordinate from the larger co-ordinate.

∵71 , d(A,B) = 7-1 = 6.

Hence d(A,B) is 6.

(ii)Co-ordinate of A = 6

Co-ordinate of B = -2

The distance between two points is obtained by subtracting the smaller co-ordinate from the larger co-ordinate.

∵6-2 , d(A,B) = 6-(-2) = 6+2 = 8.

Hence d(A,B) is 8.

(iii)Co-ordinate of A = -3

Co-ordinate of B = 7

The distance between two points is obtained by subtracting the smaller co-ordinate from the larger co-ordinate.

∵7-3 , d(A,B) = 7-(-3) = 7+3 = 10.

Hence d(A,B) is 10.

(iv)Co-ordinate of A = -4

Co-ordinate of B = -5

The distance between two points is obtained by subtracting the smaller co-ordinate from the larger co-ordinate.

∵-4-5 , d(A,B) = -4-(-5) = -4+5 = 1

Hence d(A,B) is 1.

(v)Co-ordinate of A = -3

Co-ordinate of B = -6

The distance between two points is obtained by subtracting the smaller co-ordinate from the larger co-ordinate.

∵-3-6 , d(A,B) = -3-(-6) = -3+6 = 3.

Hence d(A,B) is 3.

(vi)Co-ordinate of A = 4

Co-ordinate of B = -8

The distance between two points is obtained by subtracting the smaller co-ordinate from the larger co-ordinate.

∵4-8 , d(A,B) = 4-(-8) = 4+8 = 12.

Hence d(A,B) is 12.

3. From the information given below, find which of the point is between the other two. If the points are not collinear, state so.

(i) d(P, R) = 7, d(P, Q) = 10, d(Q, R) = 3

(ii) d(R, S) = 8, d(S, T) = 6, d(R, T) = 4

(iii) d(A, B) = 16, d(C, A) = 9, d(B, C) = 7

Solution:

(i)Given d(P, R) = 7

d(P, Q) = 10

d(Q, R) = 3

d(P,Q) = 10 …….(i)

d(P, R)+ d(Q, R) = 7+3 = 10……(ii)

d(P,Q) = d(P, R)+ d(Q, R) [from (i) and (ii)]

The points P,Q and R are collinear.

Hence R is the point between P and Q.

(ii)Given d(R, S) = 8

d(S, T) = 6

d(R, T) = 4

d(R, S) = 8 …….(i)

d(S, T) +d(R, T) = 6+4 = 10…….(ii)

d(R, S) ≠ d(S, T) +d(R, T) [from (i) and (ii)]

The points R,S and T are not collinear.

(iii) Given d(A, B) = 16

d(C, A) = 9

d(B, C) = 7

d(A, B) = 16…….(i)

d(C, A)+ d(A, B) = 9+7 = 16 …..(ii)

d(A, B) = d(C, A)+ d(A, B) [from (i) and (ii)]

The points A,B and C are collinear.

Hence A is the point between B and C.

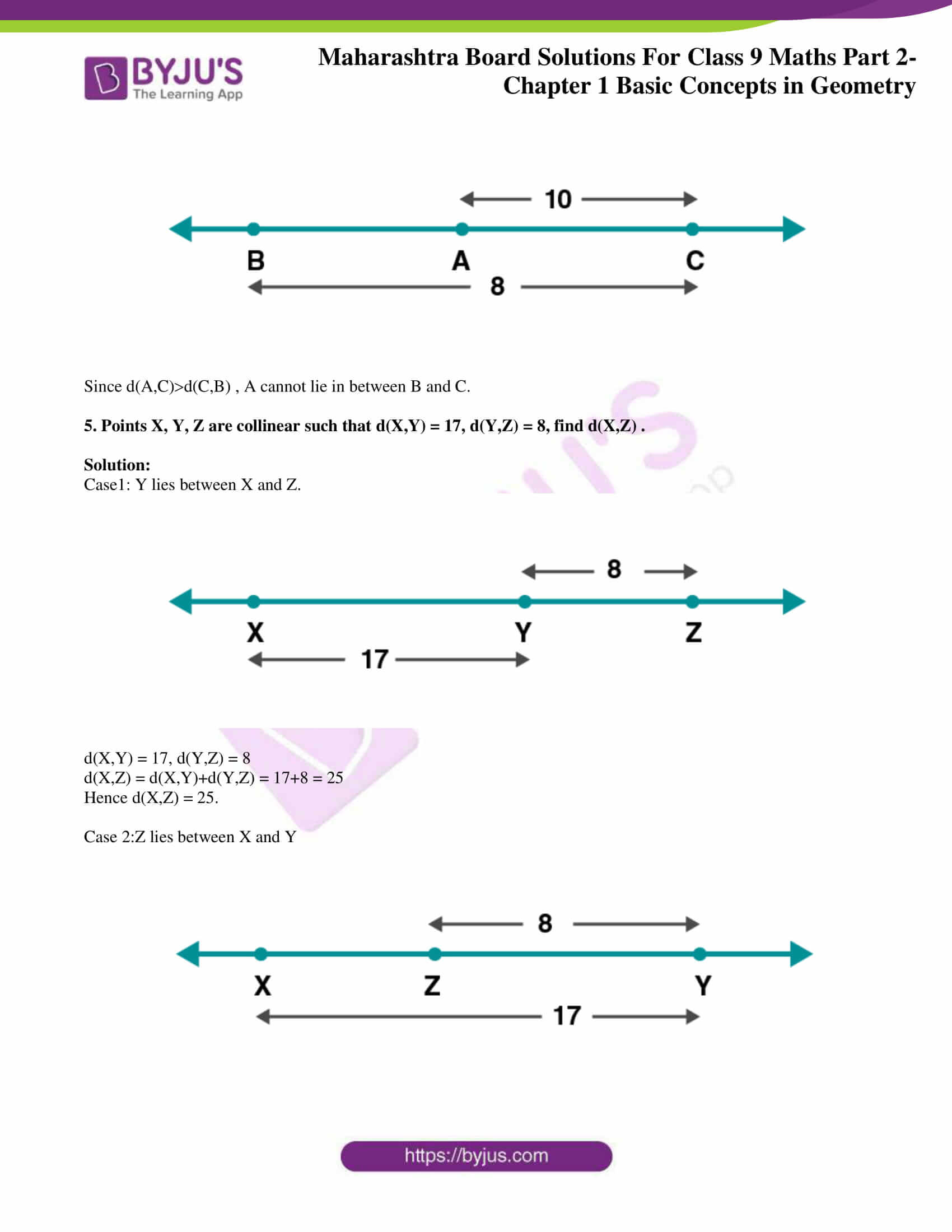
4. On a number line, points A, B and C are such that d(A,C) = 10, d(C,B) = 8 Find d(A, B) considering all possibilities.

Solution:

Case 1: C lies between A and B. ie A-C-B

d(A,C) = 10

d(C,B) = 8

d(A,B) = d(A,C)+d(C,B)

d(A,B) = 10+8 = 18

Case2: B lies between A and C. ie A-B-C

d(A,C) = 10

d(C,B) = 8

d(A,B) = d(A,C)-d(C,B)

d(A,B) = 10-8 = 2.

Case3:A lies between B and C . ie B-A-C

Since d(A,C)d(C,B) , A cannot lie in between B and C.

5. Points X, Y, Z are collinear such that d(X,Y) = 17, d(Y,Z) = 8, find d(X,Z) .

Solution:

Case1: Y lies between X and Z.

d(X,Y) = 17, d(Y,Z) = 8

d(X,Z) = d(X,Y)+d(Y,Z) = 17+8 = 25

Hence d(X,Z) = 25.

Case 2:Z lies between X and Y

d(X,Z) = d(X,Y)-d(Y,Z) = 17-8 = 9

Hence d(X,Z) = 9

Case3:X lies between Y and Z

Since d(X,Y)d(Y,Z) , X cannot lie in between Y and Z.

6. Sketch proper figure and write the answers of the following questions.

(i) If A – B – C and l(AC) = 11, l(BC) = 6.5, then l(AB) =?

(ii) If R – S – T and l(ST) = 3.7, l(RS) = 2.5, then l(RT) =?

(iii) If X – Y – Z and l(XZ) = 3√7 , l(XY) = √7 , then l(YZ) =?

Solution:

(i)Given l(AC) = 11, l(BC) = 6.5

l(AB) = l(AC)- l(BC) [A-B-C]

= 11-6.5 = 4.5

Hence l(AB) = 4.5

(ii) Given l(ST) = 3.7, l(RS) = 2.5

l(RT) = l(ST)+l(RS) [R-S-T]

= 3.7+2.5= 6.2

Hence l(RT) = 6.2

(iii) Given l(XZ) = 3√7 , l(XY) = √7

l(YZ) = l(XZ)-l(XY) [X-Y-Z]

= 3√7 -√7

= 2√7

Hence l(YZ) = 2√7

7. Which figure is formed by three non-collinear points ?

Solution:

A triangle is formed by joining three non – collinear points.

Practice Set 1.2 Page 7

1.The following table shows points on a number line and their co-ordinates. Decide whether the pair of segments given below the table are congruent or not.

(i) seg DE and seg AB (ii) seg BC and seg AD

(ii) seg BC and seg AD

(iii) seg BE and seg AD

Solutions:

(i) Co-ordinate of D = -7

Co-ordinate of E = 9

d(D,E) = 9-(-7) = 9+7 = 16 [∵9-7]

Co-ordinate of A = -3

Co-ordinate of B = 5

d(A,B) = 5-(-3) = 5+3 = 8 [∵5-3]

If the length of two segments is equal then the two segments are congruent.

Here d(D,E) ≠ d(A,B)

seg DE and seg AB are not congruent.

(ii) Co-ordinate of B = 5

Co-ordinate of C = 2

d(B,C) = 5-2 = 3 [∵52]

Co-ordinate of A = -3

Co-ordinate of D = -7

d(A,D) = -3-(-7) = -3+7 = 4 [∵-3-7]

If the length of two segments is equal then the two segments are congruent.

Here d(B,C) ≠ d(A,D)

seg BC and seg AD are not congruent.

2. Point M is the midpoint of seg AB. If AB = 8 then find the length of AM.

Solution:

If M is the midpoint of AB ,then seg AM seg MB.

Given AB = 8

AM = (1/2)AB = 8/2 = 4.

Hence AM is 4 units.

3. Point P is the midpoint of seg CD. If CP = 2.5, find l(CD).

Solution:

If P is the midpoint of CD ,then seg CP seg PD.

Given CP = 2.5

PD = 2.5

CD = CP+PD = 2.5+2.5 = 5

Hence l(CD) is 5 units.

4. If AB = 5 cm, BP = 2 cm and AP = 3.4 cm, compare the segments.

Solution:

If length of segment AB is less than the length of segment CD, it is written as seg AB < seg CD or seg CD > seg AB.

Given AB = 5 cm, BP = 2 cm and AP = 3.4 cm

53.42

seg AB seg AP seg BP

5. Write the answers to the following questions with reference to figure 1.13.

(i) Write the name of the opposite ray of ray RP

(ii) Write the intersection set of ray PQ and ray RP.

(iii) Write the union set of ray PQ and ray QR.

(iv) State the rays of which seg QR is a subset.

(v) Write the pair of opposite rays with common end point R.

(vi) Write any two rays with common end point S.

(vii) Write the intersection set of ray SP and ray ST.

Solution:

(i)The ray opposite to ray RP is ray RT or RS.

(ii)The ray is RQ.

(iii)The union set of ray PQ and RP is line RQ.

(iv)Ray QR is a subset of ray QS and ray QT.

(v)Ray RT and ray RQ , Ray RS and ray RP have common end point R.

(vi)Ray ST and ray SR have common end point S.

(vii)Intersection ser of ray SP and ray ST is point S.

6. Answer the questions with the help of figure 1.14.

(i) State the points which are equidistant from point B.

(ii) Write a pair of points equidistant from point Q.

(iii) Find d (U,V), d (P,C), d (V,B), d (U, L).

Solution:

(i)From figure d(A,B) = d(C,B ) = 2

A and C are equidistant from B.

d(B,D) = d(B,P) = 4

D and P are equidistant from B.

(ii)From figure d(Q,R) = d(Q,P) = 2

P and R are equidistant from Q.

d(Q,U) = d(Q,L) = 1

U and L are equidistant from Q.

Practice Set 1.3 Page 11

1. Write the following statements in ‘if-then’ form.

(i) The opposite angles of a parallelogram are congruent.

(ii) The diagonals of a rectangle are congruent.

(iii) In an isosceles triangle, the segment joining the vertex and the mid point of the base is perpendicular to the base.

Solution:

(i) If a quadrilateral is a parallelogram, then the opposite angles of that quadrilateral are congruent.

(ii) If a quadrilateral is a rectangle, then the diagonals are congruent.

(iii) If a triangle is an isosceles triangle, then segment joining the vertex of a triangle and midpoint of the base is perpendicular to the base.

2. Write converses of the following statements.

(i) The alternate angles formed by two parallel lines and their transversal are congruent.

(ii) If a pair of the interior angles made by a transversal of two lines are supplementary then the lines are parallel.

(iii) The diagonals of a rectangle are congruent.

Solution:

(i) If the alternate angles made by two lines and their transversal are congruent, then the two lines are parallel.

(ii) If two parallel lines are intersected by a transversal, then the interior angles formed bv the transversal are supplementary.

(iii) If the diagonals of a quadrilateral are congruent, then the quadrilateral is a rectangle.

Problem Set 1 Page 11

1.Select the correct alternative from the answers of the questions given below.

(i) How many mid points does a segment have ?

(A) only one (B) two (C) three (D) many

Solution:

A segment have only one midpoint.

Hence Option A is the answer.

(ii) How many points are there in the intersection of two distinct lines ?

(A) infinite (B) two (C) one (D) not a single

Solution:

Two distinct lines meet at one point.

Hence Option C is the answer.

(iii) How many lines are determined by three distinct points?

(A) two (B) three (C) one or three (D) six

Solution:

If three points are collinear , then one line is formed by them.

If three points are non-collinear, then three lines are formed by them.

Hence Option C is the answer.

(iv) Find d(A, B), if co-ordinates of A and B are – 2 and 5 respectively.

(A) – 2 (B) 5 (C) 7 (D) 3

Solution:

d(A,B) = 5-(-2) = 7

Hence Option C is the answer.

(v) If P – Q – R and d(P,Q) = 2, d(P,R) = 10, then find d(Q,R).

(A) 12 (B) 8 (C) 96 (D) 20

Solution:

d(Q,R) = d(P,R)-d(P,Q) = 10-2 = 8

Hence Option B is the answer.

2. On a number line, co-ordinates of P, Q, R are 3, – 5 and 6 respectively. State with reason whether the following statements are true or false.

(i) d(P,Q) + d(Q,R) = d(P,R)

(ii) d(P,R) + d(R,Q) = d(P,Q)

(iii) d(R,P) + d(P,Q) = d(R,Q)

(iv) d(P,Q) – d(P,R) = d(Q,R)

Solution:

From figure, co-ordinate of P = 3

Co-ordinate of R = 6

Here 63

d(P,R) = 6-3 = 3…………….(i)

Co-ordinate of P = 3

Co-ordinate of Q = -5

Here 3-5

d(P,Q) = 3-(-5) = 3+5 = 8………(ii)

Co-ordinate of Q = -5

Co-ordinate of R = 6

Here 6-5

d(Q,R) = 6-(-5) = 6+5 = 11………(iii)

(i) d(P,Q) + d(Q,R) = 8+11

= 17 ≠ d(P,R) [from (i)]

Hence statement is False.

(ii) d(P,R) + d(R,Q) = 3+11

= 14 ≠ d(P,Q) [from (ii)]

Hence statement is False.

(iii) d(R,P) + d(P,Q) = 3+8

= 11 = d(R,Q) [from (iii)]

Hence statement is True.

(iv) d(P,Q) – d(P,R) = 8-3

= 5 ≠ d(Q,R) [from (iii)]

Hence statement is False.

3. Co-ordinates of some pairs of points are given below. Hence find the distance between each pair.

(i) 3, 6

(ii) – 9, – 1

(iii) – 4, 5

Solution:

(i) Co-ordinates of points are 3 and 6.

Since 63

Distance between each pair = 6-3 = 3

(ii) Co-ordinates of points are -9 and -1.

Since -1-9

Distance between each pair = -1-(-9) = -1+9 = 8

(iii) Co-ordinates of points are -4 and 5.

Since 5-4

Distance between each pair = 5-(-4) = 5+4 = 9

4. Co-ordinate of point P on a number line is – 7. Find the co-ordinates of points on the number line which are at a distance of 8 units from point P.

Solution:

Let Q be a point on left side of P which is 8 units from P.

Then co-ordinate of Q = -7-8 = -15

Let R be a point on right side of P which is 8 units from P.

Then co-ordinate of Q = 8-7 = 1

Hence the co-ordinates which are at a distance of 8 units from P are -15 and 1.

5. Answer the following questions.

(i) If A – B – C and d(A,C) = 17, d(B,C) = 6.5 then d (A,B) = ?

Solution:

Given d(A,C) = 17

d(B,C) = 6.5

d(A,C) = d(A,B)+d(B,C) [A – B – C]

d(A,B) = d(A,C) – d(B,C)

=17-6.5 = 10.5

Hence d(A,B) is 10.5 units.

6. Co-ordinate of point A on a number line is 1. What are the co-ordinates of points on the number line which are at a distance of 7 units from A ?

Solution:

Co-ordinate of A = 1

Let C be the point at a distance 7 units on left side of A.

Then co-ordinate of C = 1-7 = -6

Let B be the point at a distance 7 units on right side of A.

Then co-ordinate of C = 1+7 = 8

Hence the co-ordinates of the points are -6 and 8.

This chapter also deals with coordinates of points and distance. In this chapter, we look at the subject of Geometry from a different point of view. The idea of conditional statements and proof comes in this chapter.

Follow BYJU’S to get more information on concepts and a greater level of understanding Basic Concepts In Geometry.