Bisection Method Questions

Bisection method questions with solutions are provided here to practice finding roots using this numerical method. In numerical analysis, the bisection method is an iterative method to find the roots of a given continuous function, which assumes positive and negative values at two distinct points in its domain.

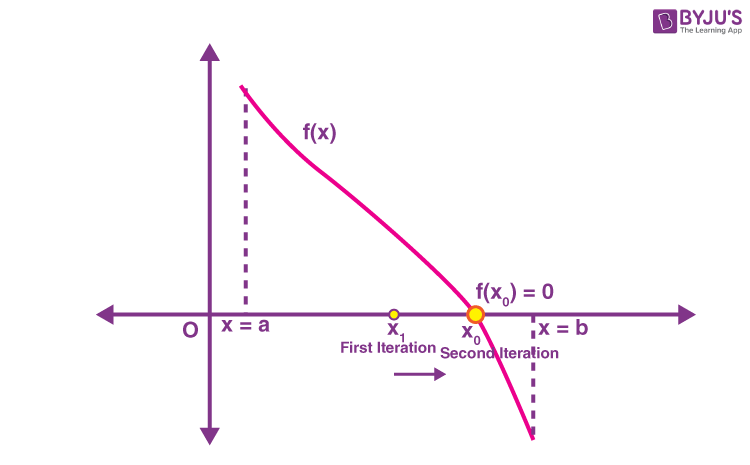
The main idea behind this root-finding method is to repeatedly bisect the interval, in which the function is continuous and assumes opposite sign values at the extremities of the interval. This process continues until we find a point x_o within the interval, for which the function vanishes.

This method is based on the intermediate value theorem for continuous functions.

Learn how to find out the roots of polynomial functions using the bisection method.

Bisection Method Questions with Solution

Follow the above algorithm of the bisection method to solve the following questions.

Question 1:

Find the root of the following polynomial function using the bisection method:

x³ – 4x – 9.

Solution:

Let f(x) = x³ – 4x – 9

f(2) = 8 – 8 – 9 = – 9

f(3) = 27 – 12 – 9 = 6

∴ the root lies in [2, 3]

First iteration:

x₁ = (2 + 3)/2 = 2.5

Now, f(x₁) = (2.5)³ – 4(2.5) – 9 = –3.375

Then, f(x₁).f(3) < 0

Thus, the root lies in [2.5, 3]

Second iteration:

x₂ = (2.5 + 3)/2 = 2.75

Now, f(x₂) = (2.75)³ – 4(2.75) – 9 = 0.7969

Then, f(x₁).f(x₂) < 0

Thus, the root lies in [2.5, 2.75]

Third iteration:

x₃ = (2.5 + 2.75)/2 = 2.625

Now, f(x₃) = (2.625)³ – 4(2.625) – 9 = –1.4121

Then, f(x₂).f(x₃) < 0

Thus, the root lies in [2.75, 2.625]

Hence, we can make the following iteration table:

∴ the root of the function is 2.707.

Question 2:

Find the root of the following polynomial function using the bisection method:

x³ – 4.

Solution:

Let f(x) = x³ – 4

f(0) = 0 – 4 = –4

f(1) = 1 – 4 = –3

f(2) = 8 – 4 = 4

∴ the root lies in [1, 2]

First iteration:

x₁ = (1 + 2)/2 = 1.5

Now, f(x₁) = (1.5)³ – 4 = –0.625

Then, f(x₁).f(2) < 0

Thus, the root lies in [1.5, 2]

Hence, we can make the following iteration table:

∴ the root of the given function is 1.59375.

Question 3:

Find the root of the following polynomial function using the bisection method:

x³ – 3.

Solution:

Let f(x) = x³ – 3

f(0) = 0 – 3 = –3

f(1) = 1 – 3 = –2

f(2) = 8 – 3 = 5

∴ the root lies in [1, 2]

First iteration:

x₁ = (1 + 2)/2 = 1.5

Now, f(x₁) = (1.5)³ – 3 = 0.375

Then, f(1).f(x₁) < 0

Thus, the root lies in [1, 1.5]

Hence, we can make the following iteration table:

∴ the root of the given function is 1.445 (approx).

Question 4:

Find the root of the following polynomial function using the bisection method:

x² – 5.

Solution:

Let f(x) = x² – 5

f(0) = 0 – 5 = –5

f(1) = 1 – 5 = –4

f(2) = 4 – 5 = –1

f(3) = 9 – 5 = 4

∴ the root lies in [2, 3]

First iteration:

x₁ = (2 + 3)/2 = 2.5

Now, f(x₁) = (2.5)² – 5 = 1.25

Then, f(2).f(x₁) < 0

Thus, the root lies in [2, 2.5].

Hence, we can make the following iteration table:

∴ the root of the given function is 2.25 (approx).

Question 5:

Find the root of the following polynomial function using the bisection method:

x³ – 3x – 5.

Solution:

Let f(x) = x³ – 3x – 5

f(2) = 8 – 6 – 5 = –3

f(3) = 27 – 9 – 5 = 13

∴ the root lies in [2, 3]

First iteration:

x₁ = (2 + 3)/2 = 2.5

Now, f(x₁) = (2.5)³ – 7.5 – 5 = 3.125

Then, f(2).f(x₁) < 0

Thus, the root lies in [2, 2.5]

Hence, we can make the following iteration table:

∴ the root of the given function is 2.2792 (approx).

Also Read:

• Fixed Point Iteration Method
• Newton Raphson Method
• False Position Method

Question 6:

Find √12.

Solution:

Let x = √12 ⇒ x² – 12 = 0

f(3) = 9 – 12 = –3

f(4) = 16 – 12 = 4

∴ the root lies in [3, 4]

First iteration:

x₁ = (3 + 4)/2 = 3.5

Now, f(x₁) = (3.5)² – 12 = 0.25

Then, f(3).f(x₁) < 0

Thus, the root lies in [3, 3.5]

Hence, we can make the following iteration table:

∴ √12 = 3.4641 (approx).

Question 7:

Find the root of the following polynomial function using the bisection method:

x⁴ – 2

Solution:

Let f(x) = x⁴ – 2

f(1) = 1 – 2 = –1

f(2) = 16 – 2 = 14

∴ the root lies in [1, 2]

Hence, we can make the following iteration table:

∴ the root of the given function is 1.19 (approx).

Question 8:

Find out after how many iterations the function x⁴ – x³– x² – 4 in the interval [1, 9].

Solution:

Let f(x) = x⁴ – x³ – x² – 4

f(1) = 1 – 1 – 1 – 4 = –5

f(9) = 6561 – 729 – 81 – 4 = 5747

First iteration:

x₁ = (1 + 9)/2 = 5

f(x₁) = 625 – 125 – 25 – 4 > 0

∴ the root lies between [1, 5]

Second iteration:

x₂ = (1 + 5)/2 = 3

f(x₁) = 81 – 27 – 9 – 4 > 0

∴ the root lies between [1, 3]

Third iteration:

x₃ = (1 + 3)/2 = 2

f(x₃) = 16 – 8 – 4 – 4 = 0

∴ x = 2 is the root of the function; hence, the iterations converges to the solution after 3 iterations.

Question 9:

For the given function f(x) = x³ – x – 1, a real root lies in between the interval [1,2]. Find the minimum number of iterations required to find the root up to the accuracy of two decimal points.

Solution:

Given,

f(x) = x³ – x² – 1

Since we have to find the root up to accuracy level of 2 decimal points, we have:

Accuracy = ε = 0.01

Now, the accuracy of the bisection method:

⇒ 0.01 ≥ 2 ^–n

⇒ 2ⁿ ≥ 100

Now, 2⁶ ≤ 100 ≤ 2⁷

∴ minimum n = 7 iterations are required.

Question 10:

For the given function f(x) = x³ – 4x + 3, a real root lies in between the interval [–3 , –2]. Find the minimum number of iterations required to find the root up to the accuracy of three decimal points.

Solution:

Given,

f(x) = x³ – 4x + 3

Since we have to find the root up to accuracy level of 2 decimal points, we have:

Accuracy = ε = 0.001

Now, the accuracy of the bisection method,

⇒ 0.001 ≥ 2 ^–n

⇒ 2ⁿ ≥ 1000

Now, 2⁹ ≤ 100 ≤ 2¹⁰

∴ minimum n = 10 iterations are required.

Practice Questions on Bisection Method

1. Solve the following using the bisection method:

(i) x² – 2

(ii) x³ – 5

(iii) x³ – x – 1

(iv) 2x³ – 2x – 5

(v) x² – 3

2. Find out after how many iterations the function 3x² – 5x – 2 in the interval [0, 4].

To learn about more numerical methods – concepts and questions, download BYJU’S – The Learning App today, and register yourself to explore video lessons, notes, and many more study resources.