Quadratics or Quadratic Equations

Quadratics can be defined as a polynomial equation of a second degree, which implies that it comprises a minimum of one term that is squared. It is also called quadratic equations. The general form of the quadratic equation is: 

ax² + bx + c = 0

where x is an unknown variable and a, b, c are numerical coefficients. For example, x² + 2x +1 is a quadratic or quadratic equation. Here, a ≠ 0 because if it equals zero then the equation will not remain quadratic anymore and it will become a linear equation, such as: 

bx+c=0

Thus, this equation cannot be called a quadratic equation.

The terms a, b and c are also called quadratic coefficients. 

The solutions to the quadratic equation are the values of the unknown variable x, which satisfy the equation. These solutions are called roots or zeros of quadratic equations. The roots of any polynomial are the solutions for the given equation.

What is Quadratic Equation?

The polynomial equation whose highest degree is two is called a quadratic equation or sometimes just quadratics. It is expressed in the form of:

ax² + bx + c = 0

where x is the unknown variable and a, b and c are the constant terms.

Standard Form of Quadratic Equation

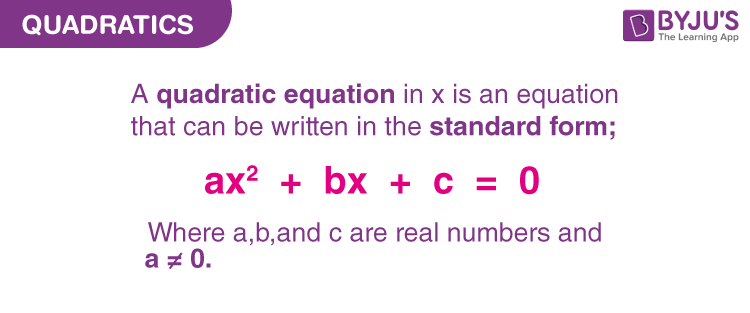
Since the quadratic includes only one unknown term or variable, thus it is called univariate. The power of variable x is always non-negative integers. Hence the equation is a polynomial equation with the highest power as 2.

The solution for this equation is the values of x, which are also called zeros. Zeros of the polynomial are the solution for which the equation is satisfied. In the case of quadratics, there are two roots or zeros of the equation. And if we put the values of roots or x on the left-hand side of the equation, it will equal to zero. Therefore, they are called zeros.

Quadratics Formula

The formula for a quadratic equation is used to find the roots of the equation. Since quadratics have a degree equal to two, therefore there will be two solutions for the equation. Suppose ax² + bx + c = 0 is the quadratic equation, then the formula to find the roots of this equation will be:

x = [-b±√(b²-4ac)]/2a

The sign of plus/minus indicates there will be two solutions for x. Learn in detail the quadratic formula here.

Examples of Quadratics

Beneath are the illustrations of quadratic equations of the form (ax² + bx + c = 0)

• x² –x – 9 = 0

• 5x² – 2x – 6 = 0

• 3x² + 4x + 8 = 0

• -x² +6x + 12 = 0

Examples of a quadratic equation with the absence of a ‘ C ‘- a constant term.

• -x² – 9x = 0

• x² + 2x = 0

• -6x² – 3x = 0

• -5x² + x = 0

• -12x² + 13x = 0

• 11x² – 27x = 0

Following are the examples of a quadratic equation in factored form

• (x – 6)(x + 1) = 0  [ result obtained after solving is x² – 5x – 6 = 0]

• –3(x – 4)(2x + 3) = 0  [result obtained after solving is -6x² + 15x + 36 = 0]

• (x − 5)(x + 3) = 0  [result obtained after solving is x² − 2x − 15 = 0]

• (x – 5)(x + 2) = 0  [ result obtained after solving is x² – 3x – 10 = 0]

• (x – 4)(x + 2) = 0  [result obtained after solving is x² – 2x – 8 = 0]

• (2x+3)(3x – 2) = 0  [result obtained after solving is 6x² + 5x – 6]

Below are the examples of a quadratic equation with an absence of linear co – efficient ‘ bx’

• 2x² – 64 = 0

• x² – 16 = 0

• 9x² + 49 = 0

• -2x² – 4 = 0

• 4x² + 81 = 0

• -x² – 9 = 0

How to Solve Quadratic Equations?

There are basically four methods of solving quadratic equations. They are:

1. Factoring
2. Completing the square
3. Using Quadratic Formula
4. Taking the square root

Factoring of Quadratics

• Begin with a equation of the form ax² + bx + c = 0
• Ensure that it is set to adequate zero.
• Factor the left-hand side of the equation by assuming zero on the right-hand side of the equation.
• Assign each factor equal to zero.
• Now solve the equation in order to determine the values of x.

Suppose if the main coefficient is not equal to one then deliberately, you have to follow a methodology in the arrangement of the factors.

Example:

2x²-x-6=0

(2x+3)(x-2)=0

2x+3=0

x=-3/2

x=2

Learn more about the factorization of quadratic equations here.

Completing the Square Method

Let us learn this method with example.

Example: Solve 2x² – x – 1 = 0.

First, move the constant term to the other side of the equation.

2x² – x = 1

Dividing both sides by 2.

x² – x/2 = ½

Add the square of half of the coefficient of x, (b/2a)2, on both the sides, i.e., 1/16

x² – x/2 + 1/16 = ½ + 1/16

Now we can factor the right side,

(x-¼)2 = 9/16 = (¾)2

Taking root on both sides;

X – ¼ = ±3/4

Add ¼ on both sides

X = ¼ ± ¾

Therefore,

X = ¼ + ¾ = 4/4 = 1

X = ¼ – ¾ = -2/4 = -½ 

To learn more about completing the square method, click here.

Using Quadratic Formula

For the given Quadratic equation of the form, ax² + bx + c = 0

Therefore the roots of the given equation can be found by:

where ± (one plus and one minus) represent two distinct roots of the given equation.

Taking the Square Root

We can use this method for the equations such as:

x² + a² = 0

Example: Solve x² – 50 = 0.

x² – 50 = 0

x² = 50

Taking the roots both sides

√x² = ±√50

x = ±√(2 x 5 x 5)

x = ±5√2

Thus, we got the required solution.

Related Articles

Video Lesson on Quadratic Equations

Range of Quadratic Equations

Solved Problems on Quadratic Equations

Lets Work Out: Example 1: \(\begin{array}{l}3x^{2} – 5x + 2 = 0\end{array} \) Solution: \(\begin{array}{l}3x^{2} – 5x + 2 = 0\end{array} \) Solving the quadratic equation using the above method: \(\begin{array}{l}x= \frac{-b \pm \sqrt{b^{2}-4ac}}{2a}\end{array} \) \(\begin{array}{l}x = \frac{-(-5)\pm \sqrt{(-5)^{2} -4 \times 3 \times 2}}{2 \times 3}\end{array} \) \(\begin{array}{l}x = \frac{5 \pm 1}{6}\end{array} \) \(\begin{array}{l}x = \frac{6}{6} \;\; or \;\; \frac{4}{6}\end{array} \) or, \(\begin{array}{l}x = 1 \;\; or \;\; \frac{2}{3}\end{array} \) Example 2: Solve x2 – 6 x = 16. Solution: x2 – 6 x = 16.  x2 – 6 x – 16 = 0 By factorisation method,  ( x – 8)( x + 2) = 0 Therefore, x = 8 and x = -2 Example 3: Solve x2 – 16 = 0. And check if the solution is correct. Solution: x2 – 16 = 0. x2 – 42 = 0  [By algebraic identities] (x-4) (x+4) = 0 x = 4 and x = -4 Check: Putting the values of x in the LHS of the given quadratic equation If x = 4 X2 – 16 = (4)2 – 16 = 16 – 16 = 0 If x = -4, X2 – 16 = (-4)2 – 16 = 16 – 16 = 0 Example 4: Solve for y: y2 = –2y + 2. Solution: Given, y2 = –2y + 2 Rewriting the given equation; y2 + 2 y – 2 = 0 Using quadratic formula, \(\begin{array}{l}y=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\end{array} \) \(\begin{array}{l}y=\frac{-(2) \pm \sqrt{(2)^{2}-4(1)(-2)}}{2(1)}\end{array} \) \(\begin{array}{l}y=\frac{-2 \pm \sqrt{4+8}}{2}\end{array} \) \(\begin{array}{l}y=\frac{-2 \pm \sqrt{12}}{2}\end{array} \) Therefore, y = -1 + √3 or y = -1 – √3

Applications of Quadratic Equations

Many real-life word problems can be solved using quadratic equations. While solving word problems, some common quadratic equation applications include speed problems and Geometry area problems.

1. Solving the problems related to finding the area of quadrilateral such as rectangle, parallelogram and so on
2. Solving Word Problems involving Distance, speed, and time, etc.,

Example: Find the width of a rectangle of area 336 cm2 if its length is equal to the 4 more than twice its width.
Solution:
Let x cm be the width of the rectangle.
Length = (2x + 4) cm
We know that
Area of rectangle = Length x Width
x(2x + 4) = 336
2x² + 4x – 336 = 0
x² + 2x – 168 = 0
x² + 14x – 12x – 168 = 0
x(x + 14) – 12(x + 14) = 0
(x + 14)(x – 12) = 0
x = -14, x = 12
Measurement cannot be negative.
Therefore, Width of the rectangle = x = 12 cm

Practice Questions

1. Solve x² + 2 x + 1 = 0.
2. Solve 5x² + 6x + 1 = 0
3. Solve 2x² + 3 x + 2 = 0.
4. Solve x² − 4x + 6.25 = 0