Simultaneous Linear Equations

In Mathematics, linear equations are the equations in which the highest power of the variable is one. The result of the linear equation is always a straight line. Thus, simultaneous linear equations are the system of two linear equations in two or three variables that are solved together to find a common solution. The simultaneous linear equation is represented as follows:

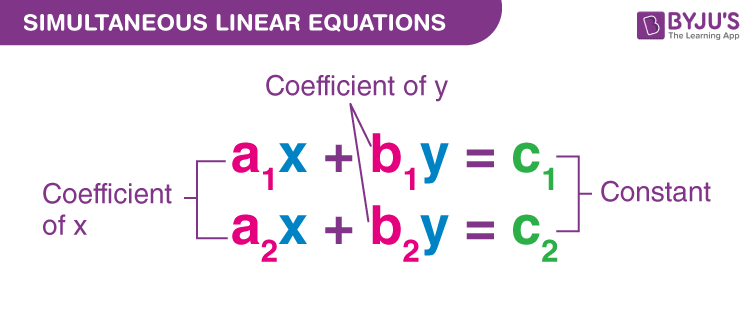
Here, a₁ and a₂ are the coefficients of x, and b₁ and b₂ are the coefficients of y, and c₁ and c₂ are constant. The solution for the system of linear equations is the ordered pair (x, y), which satisfies the given equation.

In this article, we are going to learn different methods of solving simultaneous linear equations with steps and many solved examples in detail.

Methods to Solve Simultaneous Linear Equations

Generally, three different methods are used to solve the simultaneous linear equations. They are:

• Substitution Method
• Elimination Method
• Graphical Method

Now, let us discuss all these three methods in detail with examples.

Substitution Method

Follow the below steps to solve the system of linear equations or simultaneous linear equations using the substitution method:

1. Rearrange one of the given equations to express x in terms of y.
2. Now, the expression for x can be substituted in the other equation to find the value of y.
3. Finally, substitute the value of y in any of the equations to find the value of x.

Example 1:

Solve the following system of linear equations using the substitution method:

3x – 4y = 0

9x – 8y = 12

Solution:

Given:

3x – 4y = 0 …(1)

9x – 8y = 12 …(2)

Step 1: Rearrange equation (1) to express x in terms of y:

⇒3x = 4y

⇒x = 4y/3 …(3)

Now substitute x = 4y/3 in (2), we get

⇒9(4y/3) – 8y = 12

⇒(36y/3) – 8y = 12

⇒12y – 8y = 12

⇒4y = 12

⇒y = 12/4 = 3

Hence, the value of y is 3

Now, substitute y= 3 in (3) to get the value of x

⇒ x = [4(3)]/3 = 12/3 = 4

Therefore, x = 4

Thus, the solution for the simultaneous linear equations (x, y) is (4, 3).

Elimination Method

To find the solutions (x, y) for the system of linear equations using the elimination method, go through the below steps:

1. Multiply the given equations by a constant, so as to make the coefficients of the variables in the equations equal.
2. Add or subtract the equations to eliminate the variable having the same coefficients.
3. Now, solve the equation for one variable.
4. Substitute the variable value in any of the equations to find the value of the other variable.
5. Finally, the ordered pair (x, y) is the solution of the simultaneous equation.

Example 2:

Solve the system of equations using the elimination method:

2x+3y= 11

x+2y = 7

Solution:

Given:

2x+3y= 11 …(1)

x+2y = 7 …(2)

Now, multiply the equation (2) by 2, we get

2x + 4y = 14 …(3)

Now, solve the equation (1) and (3),

2x + 3y = 11

2x + 4y = 14

–      –       –

__________

0 – y = -3

⇒ -y = -3

⇒ y = 3

Now, substitute y = 3 in equation (2),

x + 2(3) = 7

x + 6 = 7

x = 1

Hence, x = 1 and y = 3

Therefore, the solution for the system of equations 2x+3y= 11and x+2y = 7 is x = 1 and y=3.

Graphical Method

To solve the simultaneous linear equations graphically, follow the below steps:

1. First, find the coordinates of two equations simultaneously by substituting the values of x as 1, 2, 3, 4, etc.
2. Now, plot the points and we get two straight lines.
3. Observe the common point of intersection of two straight lines.
4. The common point of intersection of two straight lines is the solution of the simultaneous linear equation.

Also, read: Graphing of Linear Equations.

Example 3:

Solve the simultaneous linear equations graphically: x+y = 4 and x -y = 0.

Solution:

Given:

x+y = 4 …(1)

x -y = 0 …(2)

Let us take equation (1), x+y = 4

When x = 1,

⇒ y = 4-1 = 3

When x = 2,

⇒y= 4-2 = 2

When x = 3,

⇒ y = 4-3 = 1

Now, take the second equation x-y = 0

When x = 1,

⇒ -y = 0-1

⇒ y = 1

When x = 2,

⇒ -y = 0-2

⇒ y = 2

When x = 3,

⇒ -y = 0-3

⇒ y = 3

Now, plot these points in the XY coordinate plane.

From the graph, it is observed that the point of intersection of two straight lines is (2, 2), which is the solution for the given simultaneous linear equation.

Practice Questions

1. Solve the system of linear equations using the substitution method: 3x-2y=2 and 7x+3y=43.
2. Solve the simultaneous linear equations using the elimination method: (x/2)+(2y/3) = -1 and x – (y/3) = 3.
3. Solve the simultaneous linear equations using the graphical method: x+y = 60 and x-y = 2.

Stay tuned to BYJU’S – The Learning App, and download the app to learn all Maths concepts easily by exploring more videos.