Square root 1 to 20 are the list of values that can be squared to get the original number, respectively. For example, the square root of 4 is equal to 2 and the square of 2 is equal to 4. The square root of any number could be both positive and negative. Thus, the square of such values will always be positive. Square root 1 to 20 will include both rational and irrational numbers. You can find the square root of all the numbers from 1 to 20, here in this article.
List of Square Root 1 to 20
The table given below shows the square values from 1 to 20.
| Number (x) | Square root (√X) (Rounded to 3 Decimal Places) |
| 1 | 1.000 |
| 2 | 1.414 |
| 3 | 1.732 |
| 4 | 2.000 |
| 5 | 2.236 |
| 6 | 2.449 |
| 7 | 2.646 |
| 8 | 2.828 |
| 9 | 3.000 |
| 10 | 3.162 |
| 11 | 3.317 |
| 12 | 3.464 |
| 13 | 3.606 |
| 14 | 3.742 |
| 15 | 3.873 |
| 16 | 4.000 |
| 17 | 4.123 |
| 18 | 4.243 |
| 19 | 4.359 |
| 20 | 4.472 |
Square Root 1 to 20 Chart
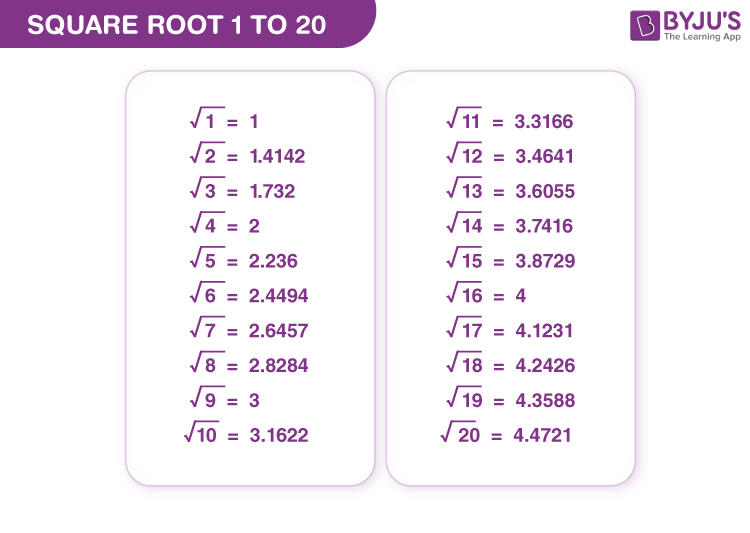
Download PDF – Square Root 1 to 20
Square Root of Perfect Squares – 1 to 20
Between 1 to 20, there are a few numbers that are perfect squares. The square root of such numbers are given in the below table.
| Square root of 1, √1 | 1 |
| Square root of 4, √4 | 2 |
| Square root of 9, √9 | 3 |
| Square root of 16, √16 | 4 |
We can see, the squares of consecutive numbers from 1 to 4 lie between 1 to 20. Hence, there are four perfect squares between 1 to 20, that are rational numbers.
Apart from these four numbers, i.e.,1, 4, 9 and 16, the square root of numbers (2, 3, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15, 17, 18, 19, 20) will all be decimal values. These decimal numbers are non-terminating and non-recurring and hence are irrational numbers.
How to Find Square Root 1 to 20?
Square root of 1 to 20 can be evaluated using two methods:
Prime factorisation is applicable for perfect squares, such as 1, 4, 9 and 16. The square root of these numbers is a whole number.
For example, prime factorisation of 9 = 3 x 3
9 = 32
Taking square root on both the sides, we get;
√9 = √32
√9 = ±3
But the numbers like 3, 5, 8, 15, etc., are not perfect squares, and the square root of such numbers cannot be determined using prime factorisation. Thus, we use the long division method to find the square root of non-perfect squares.
For example, check the square root of 10 in the below figure.

Thus, the value of √10 is 3.162, up to three places of decimal.
Related Articles
Video Lessons on Square Roots
Visualising square roots

Finding Square roots

Solved Examples on Square Root 1 to 20
Q.1: What is the sum of √1 and √9?
Solution: The value of √1 and √9 will be:
√1 = ±1
√9 = ±3
If we ignore – sign, then
√1 = 1
√9 = 3
Therefore, the sum will be 1 + 3 = 4.
Q.2: If the area of a square is 16 cm2, find the length of its side.
Solution: By the formula of area of square, we know that;
Area = side2
Thus,
Side of the square = √Area
Side = √16
Side = ±4
Length of a square cannot be negative.
Therefore, side of the square is 4 cm.
Frequently Asked Questions on Square Root 1 to 20
What is the square root of 1 to 20?
The square root 1 to 20 are the list of values of root of numbers from 1 to 20.
In square root 1 to 20, how many values are whole numbers?
In square root 1 to 20 table, there are four values that are whole numbers, such as 1, 4, 9 and 16.
How to determine the square root of 1 to 20 numbers?
We can use the prime factorisation and long division method to find the square root of 1 to 20.
Square root of which number is equal to 2?
Square root of 4 is equal to 2.
Comments