Triangles Class 9 Questions

The information provided below will help students quickly grasp a range of triangles Class 9 questions. One of the essential concepts taught in primary and secondary schools is the triangle. The triangles Class 9 questions are designed to follow the CBSE and NCERT curriculum. Students can use these questions to get a fast review of the concept of “Triangles.” Also, verify your answers by reading the detailed explanations for each question. Click here to learn more about triangles class 9.

Triangles Class 9 Questions with Solutions

1. Identify the shape of a triangle, if in ∆PQR, ∠P = ∠Q + ∠R.

Solution:

Given that, ∠P = ∠Q + ∠R

By using the angle sum property for a triangle PQR, we can write

∠P + ∠Q + ∠R = 180°

⇒ ∠P + ∠P = 180° [Since, ∠P = ∠Q + ∠R]

⇒ 2∠P = 180°

⇒ ∠P = 90°

As one of the angles equals 90°, the given triangle is a right-angled triangle.

2. Determine the measure of all the angles of an equilateral triangle.

Solution:

We know that in an equilateral triangle, all the sides must be equal.

Since the sides are equal, the angle must also be equal.

Assume that the angle of an equilateral triangle is x.

By using the angle sum property of the triangle, we can write,

x + x + x = 180°

Therefore, 3x = 180°

x = 180°/3

x = 60°

Therefore, all the angles of an equilateral triangle equal 60°.

3. Determine the measure of each of an equilateral triangle’s exterior angles.

Solution:

As we know, the relationship between the exterior angles and the interior angles of a triangle is given by:

Exterior angle + Interior angle = 180° ………(1)

As we all know, each interior angle of an equilateral triangle equals 60°.

Hence,

Exterior angle + 60° = 180°

Exterior angle = 180° – 60° = 120°

Hence, each equilateral triangle’s exterior angle = 120°.

4. Find the three equalities of the corresponding angle, if ∆ABC ≅ ∆PQR uses the SSS congruence rule.

Solution:

Using the Side – Side – Side (SSS) Congruence rule, the 3 equalities of corresponding angles are :

• ∠A = ∠P
• ∠B = ∠Q
• ∠C = ∠R

5. In ∆PQR, if PQ = PR and ∠Q = 70°, find ∠P.

Solution:

Given triangle is ∆PQR.

Also, given that PQ = PR

As we know that the angles opposite to equal sides of a triangle are equal.

So, ∠R = ∠Q

By using the angle sum property of triangle,

∠P + ∠Q + ∠R = 180°

⇒ ∠P + 70° + 70° = 180°

⇒ ∠P = 180° – 70° – 70°

⇒ ∠P = 180° – 140°

⇒ ∠P = 40°

Hence, the measure of ∠P is 40°.

6. Determine the longest side in a triangle PQR, if ∠Q = 90°.

Solution:

Since ∠Q = 90°, the given triangle is a right triangle.

If ∠Q = 90°, the side opposite to the angle Q is PR (Hypotenuse)

Therefore, the longest side of a triangle PQR is PR.

7. If PQ = 6 cm, QR = 4 cm and PR = 1.5 cm, is triangle PQR possible?

Solution:

As we know, in a triangle, the sum of lengths of any two sides is always greater than the third side.

PQ = 6cm

QR = 4cm

PR = 1.5cm

So, QR + PR = (4 + 1.5) cm

= 5.5 cm, which is less than 6 cm

Hence, the triangle PQR is not possible.

8. If ∠1 = ∠2 and ∠3 = ∠4, then prove that BC = CD, as shown in the below figure.

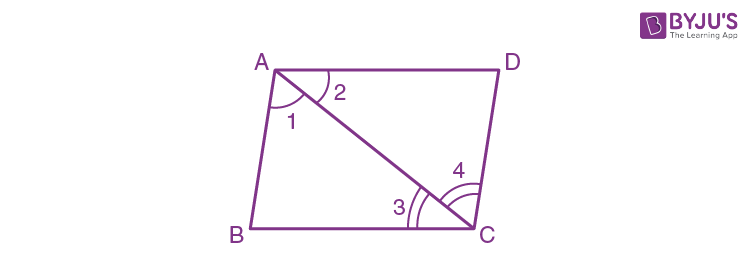
Solution:

In a triangle ABC and triangle ACD

Given that ∠1 = ∠2

Common side: AC = AC

Also, given that ∠3 = ∠4

Now, by using the Angle Side Angle (ASA) rule, we can write

∆ABC ≅ ∆CDA

Because congruent triangles’ corresponding parts are equal, we can say BC = CD.

Hence, proved.

9. Find the three angles, if the triangle’s angle is in the ratio 1:2:3.

Solution:

Given that, the ratio of the triangle’s angle is 1:2:3.

Hence, the angles are a, 2a, and 3a.

By using the angle sum property of the triangle,

The sum of three interior angles of a triangle equals 180°

Therefore,

a + 2a + 3a = 180°

6a = 180°

a = 180°/6

a = 30°

So,

2a = 2(30)° = 60°

3a = 3(30)° = 90°

Therefore, the three angles are 30°, 60° and 90°.

10. A triangle’s first two angles are equal, while the third angle is 30 degrees greater than the first two. Determine all of the triangle’s angles.

Solution:

Let the first two angles be “a” and “a” [Since the first two angles are equal]

Also, the third angle be a + 30° [Since the 3rd angle is 30° greater than the first two angles]

By using the angle sum property of the triangle, we can write,

a + a + a + 30° = 180°

3a + 30° = 180°

3a = 180° – 30°

3a = 150°

Hence, a = 150°/3

a = 50°

Therefore, the first two angles are 50° and 50°.

Third angle = a + 30° = 50° + 30° = 80°.

Hence, the three angles are 50°, 50° and 80°.

Explore More Articles:

• Circles Questions
• Quadrilateral Questions
• Surface Area and Volume Questions
• Rectangle Questions
• Lines and Angles Questions
• Square Questions
• Functions Questions

Practice Questions

1. In a triangle, the angles are listed in ascending order of magnitude. Find the three angles if the difference between two consecutive angles is 10°.
2. (k − 40)°, (k − 20)°, and (1/2 k − 10)° are the angles of a triangle. Determine the value of k.
3. Find the shortest angle in a triangle whose angles are in the ratio 2:1:3.

Register with BYJU’S – The Learning App to explore more Maths-related articles and videos.