Probability means possibility. It is a branch of mathematics that deals with the occurrence of a random event. The value is expressed from zero to one. Probability has been introduced in Maths to predict how likely events are to happen. The meaning of probability is basically the extent to which something is likely to happen. This is the basic probability theory, which is also used in the probability distribution, where you will learn the possibility of outcomes for a random experiment. To find the probability of a single event to occur, first, we should know the total number of possible outcomes.
Learn More here: Study Mathematics
| Table of contents: |
Probability Definition in Math
Probability is a measure of the likelihood of an event to occur. Many events cannot be predicted with total certainty. We can predict only the chance of an event to occur i.e., how likely they are going to happen, using it. Probability can range from 0 to 1, where 0 means the event to be an impossible one and 1 indicates a certain event. Probability for Class 10 is an important topic for the students which explains all the basic concepts of this topic. The probability of all the events in a sample space adds up to 1.
For example, when we toss a coin, either we get Head OR Tail, only two possible outcomes are possible (H, T). But when two coins are tossed then there will be four possible outcomes, i.e {(H, H), (H, T), (T, H), (T, T)}.
Download this lesson as PDF: –Download PDF Here
Formula for Probability
The probability formula is defined as the possibility of an event to happen is equal to the ratio of the number of favourable outcomes and the total number of outcomes.
| Probability of event to happen P(E) = Number of favourable outcomes/Total Number of outcomes |
Sometimes students get mistaken for “favourable outcome” with “desirable outcome”. This is the basic formula. But there are some more formulas for different situations or events.
Solved Examples
1) There are 6 pillows in a bed, 3 are red, 2 are yellow and 1 is blue. What is the probability of picking a yellow pillow?
Ans: The probability is equal to the number of yellow pillows in the bed divided by the total number of pillows, i.e. 2/6 = 1/3.
2) There is a container full of coloured bottles, red, blue, green and orange. Some of the bottles are picked out and displaced. Sumit did this 1000 times and got the following results:
- No. of blue bottles picked out: 300
- No. of red bottles: 200
- No. of green bottles: 450
- No. of orange bottles: 50
a) What is the probability that Sumit will pick a green bottle?
Ans: For every 1000 bottles picked out, 450 are green.
Therefore, P(green) = 450/1000 = 0.45
b) If there are 100 bottles in the container, how many of them are likely to be green?
Ans: The experiment implies that 450 out of 1000 bottles are green.
Therefore, out of 100 bottles, 45 are green.
Probability Tree
The tree diagram helps to organize and visualize the different possible outcomes. Branches and ends of the tree are two main positions. Probability of each branch is written on the branch, whereas the ends are containing the final outcome. Tree diagrams are used to figure out when to multiply and when to add. You can see below a tree diagram for the coin:
Types of Probability
There are three major types of probabilities:
- Theoretical Probability
- Experimental Probability
- Axiomatic Probability
Theoretical Probability
It is based on the possible chances of something to happen. The theoretical probability is mainly based on the reasoning behind probability. For example, if a coin is tossed, the theoretical probability of getting a head will be ½.
Experimental Probability
It is based on the basis of the observations of an experiment. The experimental probability can be calculated based on the number of possible outcomes by the total number of trials. For example, if a coin is tossed 10 times and head is recorded 6 times then, the experimental probability for heads is 6/10 or, 3/5.
Axiomatic Probability
In axiomatic probability, a set of rules or axioms are set which applies to all types. These axioms are set by Kolmogorov and are known as Kolmogorov’s three axioms. With the axiomatic approach to probability, the chances of occurrence or non-occurrence of the events can be quantified. The axiomatic probability lesson covers this concept in detail with Kolmogorov’s three rules (axioms) along with various examples.
Conditional Probability is the likelihood of an event or outcome occurring based on the occurrence of a previous event or outcome.
Probability of an Event
Assume an event E can occur in r ways out of a sum of n probable or possible equally likely ways. Then the probability of happening of the event or its success is expressed as;
P(E) = r/n
The probability that the event will not occur or known as its failure is expressed as:
P(E’) = (n-r)/n = 1-(r/n)
E’ represents that the event will not occur.
Therefore, now we can say;
P(E) + P(E’) = 1
This means that the total of all the probabilities in any random test or experiment is equal to 1.
What are Equally Likely Events?
When the events have the same theoretical probability of happening, then they are called equally likely events. The results of a sample space are called equally likely if all of them have the same probability of occurring. For example, if you throw a die, then the probability of getting 1 is 1/6. Similarly, the probability of getting all the numbers from 2,3,4,5 and 6, one at a time is 1/6. Hence, the following are some examples of equally likely events when throwing a die:
- Getting 3 and 5 on throwing a die
- Getting an even number and an odd number on a die
- Getting 1, 2 or 3 on rolling a die
are equally likely events, since the probabilities of each event are equal.
Complementary Events
The possibility that there will be only two outcomes which states that an event will occur or not. Like a person will come or not come to your house, getting a job or not getting a job, etc. are examples of complementary events. Basically, the complement of an event occurring in the exact opposite that the probability of it is not occurring. Some more examples are:
- It will rain or not rain today
- The student will pass the exam or not pass.
- You win the lottery or you don’t.
Also, read:
Probability Theory
Probability theory had its root in the 16th century when J. Cardan, an Italian mathematician and physician, addressed the first work on the topic, The Book on Games of Chance. After its inception, the knowledge of probability has brought to the attention of great mathematicians. Thus, Probability theory is the branch of mathematics that deals with the possibility of the happening of events. Although there are many distinct probability interpretations, probability theory interprets the concept precisely by expressing it through a set of axioms or hypotheses. These hypotheses help form the probability in terms of a possibility space, which allows a measure holding values between 0 and 1. This is known as the probability measure, to a set of possible outcomes of the sample space.
Probability Density Function
The Probability Density Function (PDF) is the probability function which is represented for the density of a continuous random variable lying between a certain range of values. Probability Density Function explains the normal distribution and how mean and deviation exists. The standard normal distribution is used to create a database or statistics, which are often used in science to represent the real-valued variables, whose distribution is not known.
Probability Terms and Definition
Some of the important probability terms are discussed here:
| Term | Definition | Example |
|---|---|---|
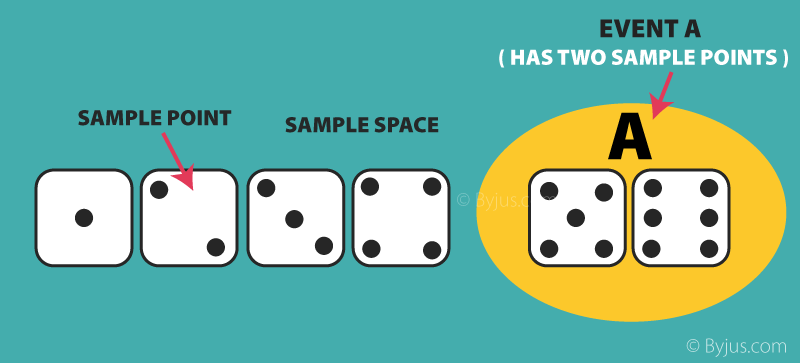
| Sample Space | The set of all the possible outcomes to occur in any trial |
|
| Sample Point | It is one of the possible results | In a deck of Cards:
|
| Experiment or Trial | A series of actions where the outcomes are always uncertain. | The tossing of a coin, Selecting a card from a deck of cards, throwing a dice. |
| Event | It is a single outcome of an experiment. | Getting a Heads while tossing a coin is an event. |
| Outcome | Possible result of a trial/experiment | T (tail) is a possible outcome when a coin is tossed. |
| Complimentary event | The non-happening events. The complement of an event A is the event, not A (or A’) | In a standard 52-card deck, A = Draw a heart, then A’ = Don’t draw a heart |
| Impossible Event | The event cannot happen | In tossing a coin, impossible to get both head and tail at the same time |
Applications of Probability
Probability has a wide variety of applications in real life. Some of the common applications which we see in our everyday life while checking the results of the following events:
- Choosing a card from the deck of cards
- Flipping a coin
- Throwing a dice in the air
- Pulling a red ball out of a bucket of red and white balls
- Winning a lucky draw
Other Major Applications of Probability
- It is used for risk assessment and modelling in various industries
- Weather forecasting or prediction of weather changes
- Probability of a team winning in a sport based on players and strength of team
- In the share market, chances of getting the hike of share prices
Problems and Solutions on Probability
Question 1: Find the probability of ‘getting 3 on rolling a die’.
Solution:
Sample Space = S = {1, 2, 3, 4, 5, 6}
Total number of outcomes = n(S) = 6
Let A be the event of getting 3.
Number of favourable outcomes = n(A) = 1
i.e. A = {3}
Probability, P(A) = n(A)/n(S) = 1/6
Hence, P(getting 3 on rolling a die) = 1/6
Question 2: Draw a random card from a pack of cards. What is the probability that the card drawn is a face card?
Solution:
A standard deck has 52 cards.
Total number of outcomes = n(S) = 52
Let E be the event of drawing a face card.
Number of favourable events = n(E) = 4 x 3 = 12 (considered Jack, Queen and King only)
Probability, P = Number of Favourable Outcomes/Total Number of Outcomes
P(E) = n(E)/n(S)
= 12/52
= 3/13
P(the card drawn is a face card) = 3/13
Question 3: A vessel contains 4 blue balls, 5 red balls and 11 white balls. If three balls are drawn from the vessel at random, what is the probability that the first ball is red, the second ball is blue, and the third ball is white?
Solution:
Given,
The probability to get the first ball is red or the first event is 5/20.
Since we have drawn a ball for the first event to occur, then the number of possibilities left for the second event to occur is 20 – 1 = 19.
Hence, the probability of getting the second ball as blue or the second event is 4/19.
Again with the first and second event occurring, the number of possibilities left for the third event to occur is 19 – 1 = 18.
And the probability of the third ball is white or the third event is 11/18.
Therefore, the probability is 5/20 x 4/19 x 11/18 = 44/1368 = 0.032.
Or we can express it as: P = 3.2%.
Question 4: Two dice are rolled, find the probability that the sum is:
- equal to 1
- equal to 4
- less than 13
Solution:
Video Lectures
Introduction

Solving Probability Questions

Probability Important Topics

Probability Important Questions

Probability Problems
- Two dice are thrown together. Find the probability that the product of the numbers on the top of the dice is:
(i) 6 (ii) 12 (iii) 7 - A bag contains 10 red, 5 blue and 7 green balls. A ball is drawn at random. Find the probability of this ball being a
(i) red ball (ii) green ball (iii) not a blue ball - All the jacks, queens and kings are removed from a deck of 52 playing cards. The remaining cards are well shuffled and then one card is drawn at random. Giving ace a value 1 similar value for other cards, find the probability that the card has a value
(i) 7 (ii) greater than 7 (iii) less than 7 - A die has its six faces marked 0, 1, 1, 1, 6, 6. Two such dice are thrown together and the total score is recorded.
(i) How many different scores are possible?
(ii) What is the probability of getting a total of 7?
Frequently Asked Questions (FAQs) on Probability
What is probability? Give an example
What is the formula of probability?
What are the different types of probability?
Theoretical Probability
Experimental Probability
Axiomatic Probability
What are the basic rules of probability?
P ( A ∪ B ) = P ( A ) + P ( B ) − P ( A ∩ B )
P ( A ∩ B ) = P ( B ) ⋅ P ( A | B )
What is the complement rule in probability?
In probability, the complement rule states that “the sum of probabilities of an event and its complement should be equal to 1”. If A is an event, then the complement rule is given as:
P(A) + P(A’) = 1.
What are the different ways to present the probability value?
The three ways to present the probability values are:
- Percentage
- Ratio
- Decimal or fraction
What does the probability of 0 represent?
The probability of 0 represents that the event will not happen or that it is an impossible event.
What is the sample space for tossing two coins?
The sample space for tossing two coins is:
S = {HH, HT, TH, TT}



good basics concepts provide
Great video content. Perfectly explained for examinations. I really like to learn from BYJU’s
Thank you for your best information on probablity
Good explanation about probability and concept for simple understanding the overall chapter. I hope this is a good way to understand the CONCEPT
For learner of class X standard , it is providing all the relevant informations and approach towards the contenet is knitted in an elegant manner and students will have the opportunity to grasp the topic easily and will be immensely benefited.
this topic has been hard for me but now I know what it is all about and I have really enjoyed it thanks for your good explanation
Well explained
Excellent explanation of probability. One can easily understand about the probability.
I really appreciated your explanations because it’s well understandable Thanks
Love the way you teach
There are 3 boxes Box A contains 10 bulbs out of which 4 are dead box b contains 6 bulbs out of which 1 is dead box c contains 8 bulbs out of which 3 are dead. If a dead bulb is picked at random find the probability that it is from which box?
Probability of selecting a dead bulb from the first box = (1/3) x (4/10) = 4/30
Probability of selecting a dead bulb from the second box = (1/3) x (1/6) = 1/18
Probability of selecting a dead bulb from the third box = (1/3) x (3/8) = 3/24 = 1/8
Total probability = (4/30) + (1/18) + (1/8)
= (48 + 20 + 45)360
=113/360