Geometry is a branch of mathematics that deals with the study of shapes and their measurements. It also focuses on the relative configuration of the shapes and their spatial properties. We know that geometry is classified into 2D Geometry and 3D Geometry. Before dividing that, all the geometrical shapes are formed by points, lines, rays and plane surface. When the two lines or the rays converge at a common point, the measurement between the two lines is called an “Angle”. In this article, we are going to discuss what is an angle, what are the different types of angles with their meaning with examples.
Table of Contents:
Angle Definition in Maths
What is an angle? In Plane Geometry, a figure which is formed by two rays or lines that shares a common endpoint is called an angle. The word “angle” is derived from the Latin word “angulus”, which means “corner”. The two rays are called the sides of an angle, and the common endpoint is called the vertex. The angle that lies in the plane does not have to be in the Euclidean space. In case if the angles are formed by the intersection of two planes in the Euclidean or the other space, the angles are considered dihedral angles. The angle is represented using the symbol “∠”. The angle measurement between the two rays can be denoted using the Greek letter θ, α, β etc. If the angles are measured from a line, we can find two different types of angles, such as a positive angle and a negative angle.
Positive Angle: If the angle goes in counterclockwise, then it is called a positive angle.
Negative Angle: If the angle goes clockwise direction, then it is called a negative angle.

How to Label the Angles?
There are two different ways to label the angles. They are:
Method 1: Give a name to the angle. Generally, the angle is named using the lower case letter like “a”, “x”, etc or by using the Greek Letters alpha (α), beta (β), theta (θ), etc.
Method 2: By using the three letters on the shapes, we can define the angle. The middle letter should be the vertex (actual angle).
For example, ABC is a triangle. To represent the angle A is equal to 60 degrees, we can define it as ∠BAC = 60°
How to Measure the Angle?
The angles are generally measured in degrees (°). An important geometrical tool that helps to measure the angles in degree is a “protractor”. A protractor has two sets of numbers going in opposite directions. One set goes from 0 to 180 degree on the outer rim and the other set goes from 180 to 0 degree on the inner rim.
For More Information On Parts Of An Angle, Watch The Below Video:

Types of Angles
The angles are classified under the following types:
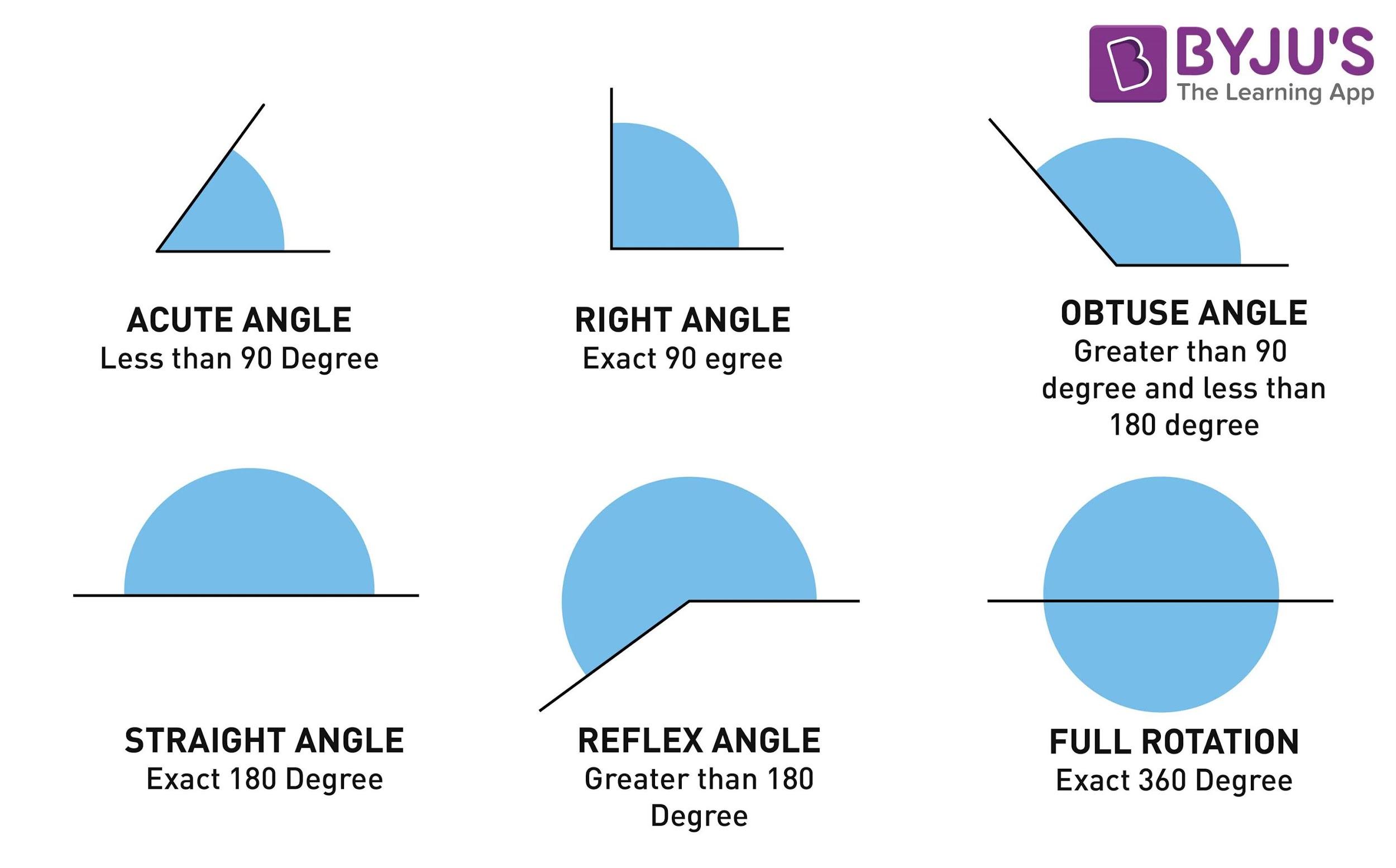
- Acute Angle – an angle measure less than 90 degrees
- Right Angle – an angle is exactly at 90 degrees
- Obtuse Angle – an angle whose measure is greater than 90 degrees and less than 180 degrees
- Straight Angle – an angle which is exactly at 180 degrees
- Reflex Angle – an angle whose measure is greater than 180 degrees and less than 360 degrees
- Full Angle – an angle whose measure is exactly at 360 degrees
Based on these angles and the lines, it is further classified into different types such as complementary angles, supplementary angles, adjacent angles, vertical angles, alternate interior angles, alternate exterior angles, and so on.
A series of angles are formed when the transversal cuts two or more lines. Specific names are given to the pair of angles, which depends on the location of the angle in relation to the lines. The lines may be either a parallel line or a not-parallel line. Some of the important pair of angles are:
- Corresponding Angles
- Alternate Interior Angles
- Alternate Exterior Angles
- Interior Angles on the Same Side of Transversal
- Supplementary Angles
- Adjacent Angles
- Vertical Angles
Now let us discuss some of the important theorems based on the lines and angles:
- If two parallel lines are cut by a transversal, then the alternate interior angles are of the same measure.
- If two parallel lines are cut by a transversal, then the alternate exterior angles are of the same measure.
- If two parallel lines are cut by a transversal, then the corresponding angles are of the same measure.
- If two parallel lines are cut by a transversal, then the interior angles on the same side of the transversal are supplementary.
- Vertical angles are congruent when the straight line intersects the lines. The lines may be either parallel or not-parallel
Properties of Angles
The following are the important properties of angles:
- The sum of all the angles on one side of a straight line is always equal to 180 degrees,
- The sum of all the angles around the point is always equal to 360 degrees.
Angle Examples
Question 1:
Find the unknown angle x for the given triangle ABC, where ∠A = 28° and ∠B = 91°
Solution:
Given that ∠A = 28° and ∠B = 91°
Let ∠C = x
We know that the sum of interior angles of a triangle is 180°
Therefore,
∠A + ∠B + ∠C = 180°
28°+ 91° + x = 180°
119° + x = 180°
x = 180° – 119°
x = 61°
Therefore, the value of the unknown angle is 61°
Question 2:
Find the unknown angle in a quadrilateral ABCD, where ∠A = 120°, ∠B = 60°, ∠C = 45°. Find the unknown angle D.
Given:
∠A = 120°
∠B = 60°
∠C = 45°
To find ∠D.
We know that the sum of the interior angles of a quadrilateral is equal to 360°.
Therefore,
∠A + ∠B + ∠C + ∠D = 360° ….(1)
Now, substitute the known values in the equation (1), we get
120° + 60°+ 45° + ∠D = 360°
225° + ∠D = 360°
∠D = 360° – 225°
∠D = 135°
Therefore, the unknown angle, ∠D is 135°
Frequently Asked Questions on Angles
Define Angle in Geometry
An angle is defined as the figure, in which two rays meet at a common point called the vertex. The angle is denoted using the symbol “∠”.
What are the different types of angles?
The different types of angles are:
Acute angle
Obtuse angle
Right angle
Reflex angle
Straight angle
Full angle
Mention the properties of angles
The two main important properties of angles are:
The sum of all the angles on one side of a straight line always measures 180 degrees.
The sum of all the angles around a point always measures 360 degrees.
What is meant by interior and exterior angles?
The angle which is formed on the inside of a shape is called the interior angles, whereas the angles formed on the outside of the shape are called the exterior angles.
What is meant by adjacent and vertical angles?
If two angles share a common vertex and the common arm, then the angles are called adjacent angles. Vertical angles are the angles opposite each other when two lines intersect.
Download BYJU’S – The Learning App today and subscribe to BYJU’S YouTube Channel to learn in an engaging way.


Comments