Distance formula questions with solutions are provided here for students to practice and understand how to find the distance between the two points in a Cartesian plane.
In coordinate geometry, the distance between two points A(x1, y1) and B(x2, y2) is given by
This formula is used to find the distance between two points in a two-dimensional plane.
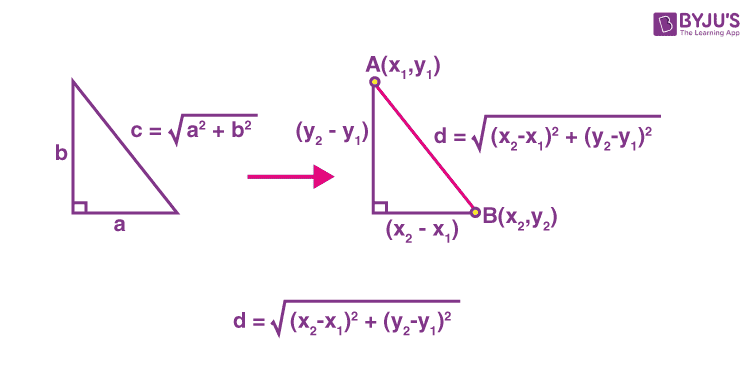
The distance between two points A(x1, y2, z1) and B(x2, y2, z2) in three dimensional plane is given by –
To see the derivation of the distance formula, click here.
Distance Formula Questions with Solutions
Let us apply the distance formula by solving some questions.
Question 1:
Find the distance between the following points:
(I) (-1, 2) and (2, 3)
(II) (0, 1) and (6, –1)
(III) (1, 0, –1) and (2, 0, 7)
Solution:
(I) Let the distance between the points (-1, 2) and (2, 3) be d, then
d = √[(2 – ( –1))2 + (3 – 2)2] = √[9 + 1] = √10 units.
(II) Let the distance between the points (0, 1) and (6, –1) be d, then
d = √[(6 – 0)2 + ( –1 – 1)2] = √[36 + 4] = √40 = 2√10 units.
(III) Let the distance between the points (1, 0, –1) and (2, 0, 7) be d, then
d = √[(2 – 1)2 + (0 – 0)2 + (7 – ( –1))2] = √[1 + 0 + 64] = √65 units.
Question 2:
Find a point on the x-axis which is equidistant from the points ( –5, 2) and (9, –2).
Solution:
Let the points be P( –5, 2) and Q(9, –2) and let R(x , 0) be the point on x-axis which is equidistant from P and Q.
Now, PR = QR ⇒ PR2 = QR2
⇒ [(x – ( –5))2 + (0 – 2)2] = [(x – 9)2 + (0 – ( –2))2]
⇒ (x + 5)2 + 4 = (x – 9)2 + 4
⇒ x2 + 10x + 25 = x2 – 18x + 81
⇒ 10x + 18x = 81 – 25
⇒ 28x = 56
⇒ x = 56/28 = 2
Therefore, the point is R(2, 0).
Question 3:
Show that the points P( –1, 6, 6), Q(0, 7, 10) and R( –4, 9, 6) form an isosceles right triangle.
Solution:
Now, PQ = √[(0 +1)2 + (7 – 6)2 + (10 – 6)2]
= √[1 + 1 + 16] = √18 = 3√2 units.
QR = √[( –4 – 0)2 + (9 – 7)2 + (6 – 10)2]
= √[16 + 4 + 16] = √36 = 6 units.
PR = √[( –4 – ( –1))2 + (9 – 6)2 + (6 – 6)2]
= √[9 + 9 + 0] = √18 = 3√2 units.
Also, PQ2 + PR2 = QR2. Hence, PQR is a right isosceles triangle.
|
Collinearity of Points If A(x1, y1), B(x2, y2), and C(x3, y3) are collinear points on a plane, then the sum of any two of these distances is equal to the third distance. That is, AB + BC = AC Or, AB + AC = BC Or, AC + BC = AB |
Question 4:
Show that the points A(2, 3), B(3, 4) and C(4, 5) are collinear.
Solution:
Now, AB = √[(3 – 2)2 + (4 – 3)2]
= √[1 + 1] =√2 units
BC = √[(4 – 3)2 + (5 – 4)2]
= √[1 + 1] = √2 units
AC = √[(4 –2)2 + (5 – 3)2]
= √[22. + 22] = √8 = 2√2 units.
Clearly, AB + BC = AC
∴ the points are collinear.
Question 5:
The vertices of a triangle ABC are A(1, 2), B(3, –4), and C(5, –6). Find its circumcentre and circum-radius.
Solution:
The circumcentre of a triangle is an interior point of a triangle equidistant from the vertices of the triangle, and the circum-radius is that equal distance.
Let O(x, y) be the circumcentre of the triangle ABC. the
AO = BO = CO ⇒ AO2 = BO2 = CO2
Taking
AO2 = BO2
⇒ (x – 1)2 + (y – 2)2 = (x – 3)2 + (y + 4)2
⇒ x2 – 2x + 1 + y2 – 4y + 4 = x2 – 6x + 9 + y2 + 8y + 16
⇒ 4x – 12y = 25 – 5
⇒ x – 3y = 5 ….(i)
Again taking BO2 = CO2.
⇒ (x – 3)2 + (y + 4)2 = (x – 5)2 + (y + 6)2
⇒ –6x + 8y + 10x – 12y = 25 + 36 – 9 – 16
⇒ 4x – 4y = 36
⇒ x – y = 9 ….(ii)
Subtracting (ii) from (i) we get, y = 2 and x = 11
∴ the circumcentre is O(11, 2)
And the circum-radius is AO = √[(11 – 1)2 + (2 – 2)2] = 10 units.
Also Read:
Question 6:
Find the area of the square whose one pair of opposite vertices are (3, 4) and (5, 6).
Solution:
Let ABCD be the square and let A(3, 4) and C(5, 6) be the pair of opposite vertices of the square.
Now, AC makes the diagonal of the square and the area of a square is also given by (diagonal)2/2/
AC =√[(5 – 3)2 + (6 – 4)2] = √[22 + 22] = 2√2 units
Area of the square ABCD = AC2/2 = 8/2 = 4 square units.
|
Circumcentre of a Triangle: The circumcentre of a triangle is the point inside the triangle which is equidistant from all the vertices of the triangle. Ortho-centre of a Triangle: The ortho-centre of a triangle is the point where all the three altitudes of a triangle intersect
The centroid of a Triangle: The centroid of a triangle is the intersection point of all the medians of a triangle. If A(x1, y1) , B(x2, y2) and C(x3, y3) are the vertices of triangle ABC, then the centroid of the triangle is given by ((x1 + x2 + x3)/3, (y1 + y2 + y3)/3). |
Question 7:
Find the orthocentre of the triangle ABC such that A(2, 2), B(6, 3) and C(4, 11).
Solution:
Let us find the length of each side of the triangle
AB = √[(6 – 2)2 + (3 – 2)2] = √[16 + 1] = √17 units.
BC = √[(4 – 6)2 + (11 – 3)2] = √4 + 64 = √68 units
AC = √[(4 – 2)2 + (11 – 2)2] = √[4 + 81] = √85 units
We see that AB2 + BC2 = AC2
∴ triangle ABC is a right-angled triangle at B
Thus, the ortho-centre of the triangle ABC is at B(6, 3).
Question 8:
Find the center of the circle passing through points A(0, 5), B(3, 8), and C(6, 5).
Solution:
Let O(x, y) be the center of the circle.
Then AO2 = BO2 = CO2
Taking AO2 = BO2
⇒ (x – 0)2 + (y – 5)2 = (x – 3)2 + (y – 8)2
⇒ –10y + 6x + 16y = 9 + 64 – 25
⇒ 6x + 6y = 48
⇒ x + y = 8 ….(i)
Again taking BO2 = CO2
⇒ (x – 3)2 + (y – 8)2 = (x – 6) + (y – 5)2
⇒ –6x –16y + 12x + 10y = 36 + 25 – 9 – 64
⇒ 6x – 6y = – 12
⇒ x – y = –2 ….(ii)
Adding (i) and (ii), we get
2x = 6 ⇒ x = 3 and y = 5
∴ O(3, 5) is the centre of the circle passing through points A(0, 5), B(3, 8) and C(6, 5).
Question 9:
If the point P(2, 1) lies on the line segment joining the points A(4, 2) and B(8, 4), then prove that AP = ½ AB.
Solution:
Let us find the length of AP and AB,
AP = √[(2 – 4)2 + (1 – 2)2] = √[4 + 1] = √5 units.
AB = √[(8 – 4)2 + (4 – 2)2] = √[16 + 4] = 2√5 units.
Clearly, 2AP = AB
⇒ AP = ½ AB.
Question 10:
Find the coordinates of a point that is equidistant from the three vertices of a triangle (0, 0), (0, 2y), and (2x, 0).
Solution:
Let the triangle be ABC such that A(0, 0), B(2x, 0), and C(0, 2y), and let P(h, k) be the point equidistant from all the points.
Then, PA2 = PB2 = PC2
Taking, PA2 = PB2
⇒ (h – 0)2 + (k – 0)2 = (h – 2x)2 + (k – 0)2.
⇒ h2 + k2 = h2 + 4x2 – 4hx + k2
⇒ 4hx = 4x2.
⇒ h = x
Again taking, PB2 = PC2
⇒ (h – 2x)2 + (k – 0)2 = (h – 0)2 + (k – 2y)2
⇒ h2 + 4x2 – 4hx + k2 = h2 + k2 – 4ky + 4y2
⇒ 4x2 – 4x2 = –4ky + 4y2 { ∵ h = x}
⇒ k = y
∴ the coordinates of the point are P(x, y).
Check your answers with the distance formula calculator.
<h2>Related Video Lesson</h2>
<div class=”youtube-video” data-video-thumbnail=””><img class=”tumbnailYT” src=”https://cdn1.byjus.com/wp-content/uploads/2020/01/section-formula-in-coordinate-geometry.jpg” data-video=”https://www.youtube.com/embed/KowWdT5IcaQ” /></div>
Related Articles |
|
Practice Questions on Distance Formula
1. Find the distance between the following points:
(I) (2, 5) and (3, 6)
(II) ( –9, 3) and (3, 2)
(III) (4, 5, –2) and (0, –2, 3)
2. Find a point on the y-axis which is equidistant from the points ( –5, 2) and (9, –2).
3. Find the area of the square whose one pair of opposite vertices are (2, 6) and (6, 2).
4. Find the orthocentre of the triangle PQR such that P( –1, 6, 6), Q(0, 7, 10) and R( –4, 9, 6).
5. Find the coordinates of the fourth vertex of the parallelogram whose rest of the three vertices are ( –2, 3), (6, 7) and (8, 3).
Learn about various mathematical concepts in a simple manner with detailed information, along with step-by-step solutions to all questions, only at BYJU’S. Download BYJU’S – The Learning App to get personalized videos.