In Mathematics, the centroid defines the geometric centre of a two-dimensional plane surface. It is a point that is located from the arithmetic mean position of all the points on the plane surface. Otherwise, it is defined as the average of all the points in the plane figure. The centroid can be found for different geometrical shapes. In this article, the concept of the centroid of a triangle is discussed in detail.
What is the Centroid of a Triangle?
Definition: For a two-dimensional shape “triangle,” the centroid is obtained by the intersection of its medians. The line segments of medians join vertex to the midpoint of the opposite side. All three medians meet at a single point (concurrent). The point of concurrency is known as the centroid of a triangle.

From the given figure, three medians of a triangle meet at a centroid “G”. A centroid is also known as the centre of gravity.
Properties of the Centroid of Triangle
The important properties of the centroid of a triangle are:
- The centroid of a triangle is located at the intersecting point of all three medians of a triangle
- It is considered one of the three points of concurrency in a triangle, i.e., incenter, circumcenter, centroid
- The centroid is positioned inside a triangle
- At the point of intersection (centroid), each median in a triangle is divided in the ratio of 2: 1
Centroid of a Triangle Formula
If the coordinates of the vertices of a triangle are (x1, y1), (x2, y2), (x3, y3), then the formula for the centroid of the triangle is given below:
The centroid of a triangle = ((x1+x2+x3)/3, (y1+y2+y3)/3)
Where,
x1, x2, x3 are the x coordinates of the vertices of a triangle.
y1, y2, y3 are the y coordinates of the vertices of a triangle.
Derivation for the Formula of a Triangle’s Centroid (Proof)
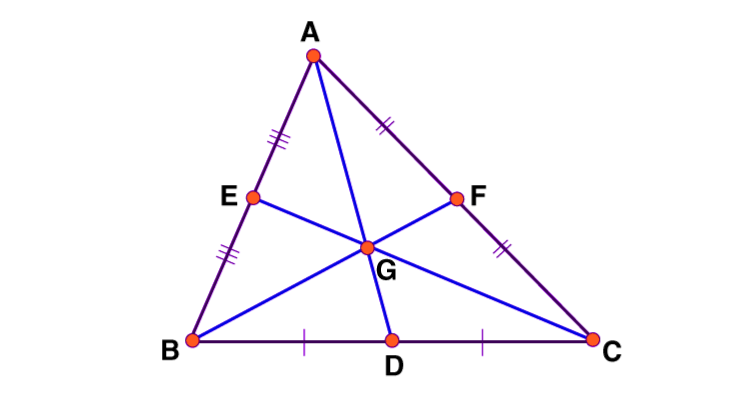
Let ABC be a triangle with the vertex coordinates A( (x1, y1), B(x2, y2), and C(x3, y3). The midpoints of the side BC, AB and AC are D, E, and F, respectively. The centroid of a triangle is represented as “G.”
As D is the midpoint of the side BC, the midpoint formula can be determined as:
((x2+x3)/2, (y2+y3)/2)
We know that point G divides the median in the ratio of 2: 1. Therefore, the coordinates of the centroid “G” are calculated using the section formula.
To find the x-coordinates of G:
x = (2(x2+x3)/2 + 1.x1 )/ (2+1)
x= (x2+x3+x1)/3
x = (x1+x2+x3)/3
To find the y-coordinates of G:
Similarly, for y-coordinates of the centroid “G.”
y =(2(y2+y3)/2 + 1.y1 )/ (2+1)
y= (y2+y3+y1)/3
y = (y1+y2+y3)/3
Therefore, the coordinates of the centroid “G” is ((x1+x2+x3)/3 , (y1+y2+y3)/3 )
Hence, proved
Try This: Centroid Calculator
Questions on Centroid of Triangles
Question: Determine the coordinates of the centroid of a triangle whose vertices are (-1, -3), (2, 1) and (8, -4)
Solution:
Given,
The vertices coordinates are (-1, -3), (2, 1) and (8, -4)
From this, we can write the x- coordinates
x1 = -1, x2 = 2, x3 = 8
Similarly, for the y-coordinates;
y1 = -3, y2 = 1, y3 = -4
The formula to find the centroid of a triangle is
G = ((x1+x2+x3)/3 , (y1+y2+y3)/3 )
Substitute the values, G = ((-1+2+8)/3 , (-3+1-4)/3)
G =( 9/3 , -6/3)
G = (3, -2)
Therefore, the centroid of a triangle, G = (3, -2)
| Also Check: | |
|---|---|
| Coordinate Geometry | Geometry |
| Types Of Triangles | Altitude And Median Of A Triangle |

