Reflection Symmetry

You may have often heard of the term ‘symmetry’ in your day-to-day life. If any object can be divided into two halves such that one half forms the mirror image of the other half, then the object is known to be Symmetrical. Whereas, if both the halves are not mirrored images of each other, then the object is said to be asymmetrical. Symmetric objects are found all around us, in nature, in architecture, in art etc. We are already aware of the different types of symmetry. In this article, we will discuss the line or reflection symmetry.

What is Reflection Symmetry?

Reflection symmetry is a type of symmetry which is with respect to reflections. Reflection symmetry is also known as line symmetry or mirror symmetry. It states that if there exists at least one line that divides a figure into two halves such that one half is the mirror image of the other half.

• The line where a mirror can be kept so that one-half appears as the reflection of the other is called the line of symmetry.
• A figure can have one or more lines of reflection symmetry.
• The line of symmetry can be in any direction.

Examples of Reflection Symmetry

• Regular polygons of N sides have N lines of symmetry.

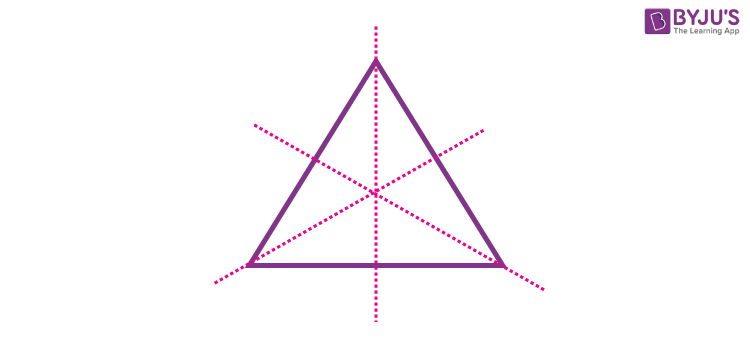
Triangle: 3 Lines of Symmetry

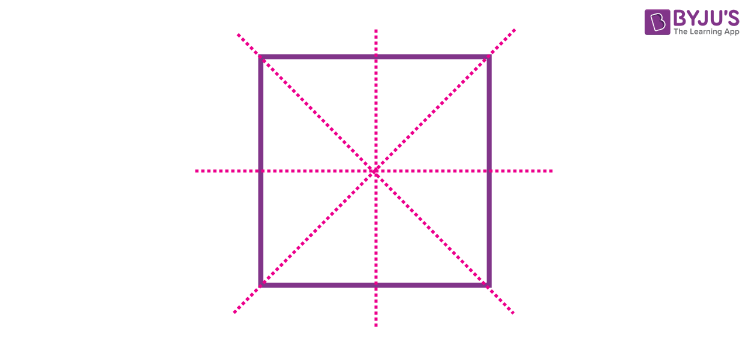
Square: 4 Lines of Symmetry

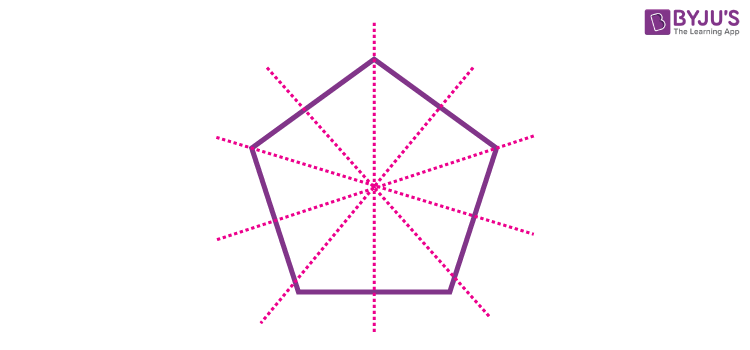
Pentagon: 5 Lines of Symmetry

• A rectangle has a vertical and a horizontal line of symmetry.

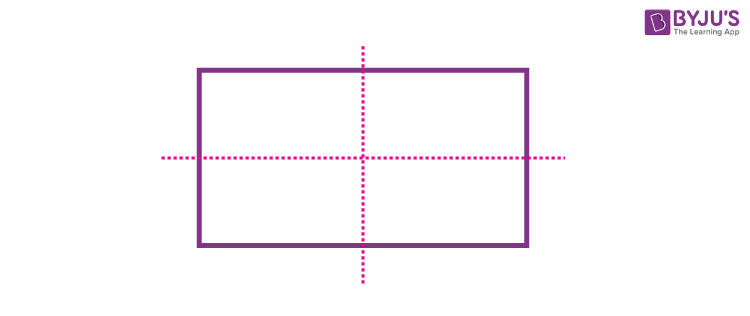
Rectangle: 2 Lines of Symmetry

However, it is not symmetrical across its diagonal.

Is Parallelogram Symmetrical?

• At first glance, a parallelogram may look symmetrical. But it is not symmetrical along any of the axes of reflection.

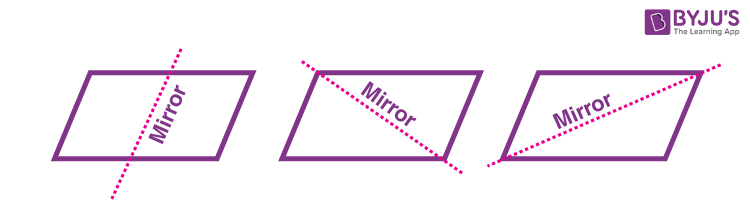
Reflection symmetry of Parallelogram

• Reflection symmetry is also observed in inkblot paper. Pour a little ink and water drop on one side of the paper. Fold the paper into two halves and press it with your palm. Unfold the paper to see the symmetric pattern along the line of the fold. The line of the fold is the axis of reflection.

To learn more about reflection symmetry, download BYJU’S The Learning App and register.