Degree and radian measure are the units of measurement of an angle that we use regularly. We know that these measures can be expressed in the form of numbers which are real. Thus, the measurement of an angle in radians is the real number for any given angle. This relation among radian and real numbers is explained here along with an illustration.
Click here to recall what real numbers are.
What is the Relationship between Radian and Real Numbers?
To establish the relationship between radian and real numbers, one should follow the below construction steps.
Step 1: Consider the unit circle with centre O.
Step 2: Locate a point, say P on the circle.
Step 3: Now, take the line segment OP as the initial side of an angle.
Step 4: From the initial side OP, the length of an arc of the circle will give the radian measure of the angle, which the arc will subtend at the centre of the circle.
Step 5: Draw the line APB, which is tangent to the circle with the point of contact P.
Step 6: Consider this line as a number line with real numbers such that the point A represents the real number zero (0), AP represents the positive real numbers, and PB represents negative real numbers, as shown in the below figure.
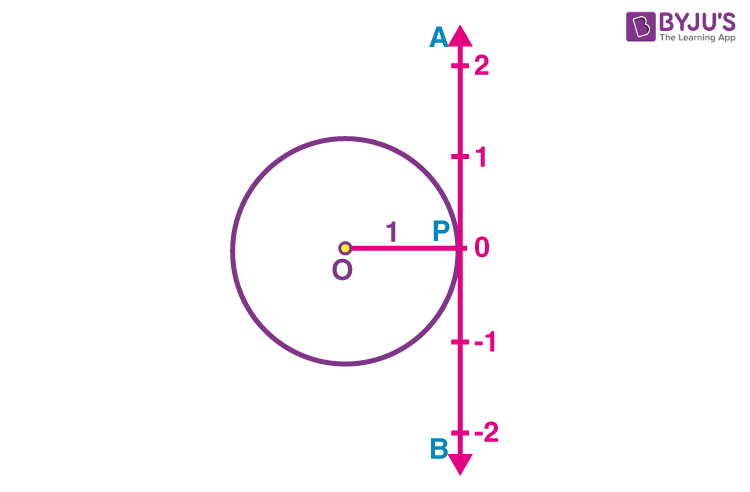
Thus, when we rope the line PA in the anticlockwise direction along the circle and PB in the clockwise direction, every real number will correspond to a radian measure and conversely.
In this way, radian measures and real numbers can be considered as the same. Hence, the numbers representing the radians are the real numbers only.
| Read more: |
To understand the above relation clearly, go through the given measurements of angles in radians and the corresponding values in degree measure.
| Radians | Degrees |
| 1 | 57.2958 or 57° 16′ |
| 5 | 286.479 |
| 10 | 572.958 |
| 20 | 1145.92 |
| 30 | 1718.87 |
| 60 | 3437.75 |
| 90 or π/2 | 5156.62 |
| π (or 22/7) | 180 |
| 2π | 360 |
In the above table, all the measures of angles in radians and degrees are real numbers.
Let us incorporate the above measures with trigonometric functions.
Suppose the sin angle for a certain measure is different for degree measurement and radian measurement.
For example, sin 18 is different from sin 18°.
Here, sin 18 means the value of sin for 18 radians, whereas sin 18° describes the value of sin for 18 degrees.
Thus, sin 18 value in radians is equal to -0.769214 (approx) and sin 18° = 0.309016995…
The value of cos 0 for degree and radians is the same, i.e. cos 0 = cos 0° = 1.
For some values of degrees and radians, the value of the given trigonometric function will be the same.
Video Lesson on Numbers

Visit byjus.com for more interesting maths articles and also download BYJU’S – The Learning App to enjoy the fun in learning maths and science concepts.
Comments