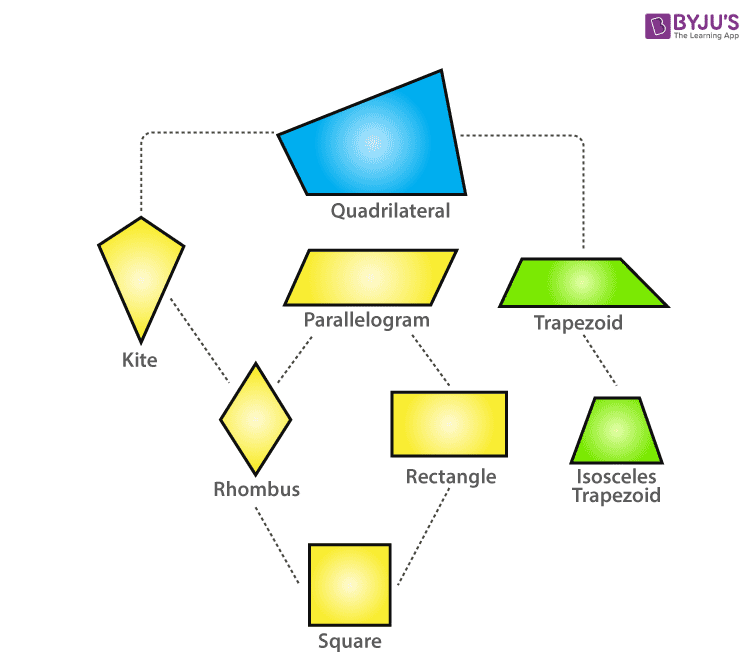
To understand rhomboids, we need to understand what a plane figure is. A plane figure can be an open or closed figure drawn using either straight line on curved lines. It is primarily a two-dimensional figure. So to understand geometry, we need to understand plane figures. They have both vertices and sides. Similarly, they have perimeters and areas but not surface area and volumes. The basic types of figures are shown in the image below.
Also check: Parallelepiped
Definition of Rhomboid
The rhomboid is different from a rhombus. It is a type of parallelogram. It is very similar to a parallelogram. It is a figure in which opposite sides are parallel to each other. This is why it is similar to a parallelogram. And if a rhomboid has all sides equal, it becomes a rhombus. So we can say that a rhombus is always a rhomboid, but all rhomboids may not be a rhombuses. The below figure is the rhomboid with base b and height or altitude h.

Rhomboid Properties
- Opposite pair of sides are parallel.

- Opposite sides of a rhomboid are also congruent.
- The diagonal divides the rhomboid into two congruent triangles.
- Opposite angles of a rhomboid are also congruent.

- The sum of interior angles of a rhomboid is equal to 360 degrees.

Important Rhomboid Formulas
- The perimeter of a rhomboid: The perimeter of a rhomboid is the sum of all sides of the figure i.e. P= (a +b + a +b) = 2(a + b), where b is the base of the rhomboid and a is the length of the other side of the rhomboid.

- Area of a rhomboid: The diagonal of a rhomboid divides the rhomboid into two congruent triangles and its area becomes ½ x base x altitude.

Where AB is the base and BD is the diagonal which divides it into two parts(equal).
Examples of a Rhomboid
Problem 1: Calculate the perimeter of the rhomboid shown below:

Solution: For the given figure above,
Base length = b = 8cm
Adjacent side = a = 7 cm
Height (altitude) = h = 4 cm
Therefore, the perimeter = 2 (a + b) cm = 2 (7 + 8) = 2(15) = 30 cm
| Related Links | |
| Area of Rhombus | Difference between Rhombus and Parallelogram |
| Construction of Rhombus | Area of Parallelogram |

