Square root of a number is a value, which on multiplication by itself, gives the original number. The square root is an inverse method of squaring a number. Hence, squares and square roots are related concepts.
Suppose x is the square root of y, then it is represented as x=√y, or we can express the same equation as x2 = y. Here, ‘√’ is the radical symbol used to represent the root of numbers. The positive number, when multiplied by itself, represents the square of the number. The square root of the square of a positive number gives the original number.
For example, the square of 3 is 9, 32 = 9 and the square root of 9, √9 = 3. Since 9 is a perfect square, hence it is easy to find the square root. But for an imperfect square like 3, 7, 5, etc., we have to use different methods to find the square root. Learn square roots from 1 to 25 with some shortcut tricks here.
| Table of Contents: |
Square Roots Definition
The square root of any number is equal to a number, which when squared gives the original number.
Let us say m is a positive integer, such that √(m.m) = √(m2) = m
In mathematics, a square root function is defined as a one-to-one function that takes a positive number as an input and returns the square root of the given input number.
f(x) = √x
For example, if x=4, then the function returns the output value as 2.
Note: The square root of a negative number represents a complex number.
Suppose √-n = i√n, where i is the imaginary number.
Square Root Symbol
The square root symbol is usually denoted as ‘√’. It is called a radical symbol. To represent a number ‘x’ as a square root using this symbol can be written as:
‘ √x ‘
where x is the number. The number under the radical symbol is called the radicand. For example, the square root of 6 is also represented as radical of 6. Both represent the same value.
Square Root Formula
The formula to find the square root is:
| y = √a |
Since, y.y = y2 = a; where ‘a’ is the square of a number ‘y’.
Properties of Square root
Some of the important properties of the square root are as follows:
- If a number is a perfect square number, then there exists a perfect square root.
- If a number ends with an even number of zeros (0’s), then it can have a square root.
- The two square root values can be multiplied. For example, √3 can be multiplied by √2, then the result should be √6.
- When two same square roots are multiplied, then the result should be a radical number. It means that the result is a non-square root number. For instance, when √7 is multiplied by √7, the result obtained is 7.
- The square root of any negative numbers is not defined because the perfect square cannot be negative.
- If a number ends with 2, 3, 7 or 8 (in the unit digit), then the perfect square root does not exist.
- If a number ends with 1, 4, 5, 6 or 9 in the unit digit, then the number may have a perfect square root.
How do Find Square Root of Numbers?
To find the square root of any number, we need to figure out whether the given number is a perfect square or an imperfect square. If the number is a perfect square, such as 4, 9, 16, etc., then we can factorize the number by prime factorisation method. If the number is an imperfect square, such as 2, 3, 5, etc., then we have to use a long division method to find the root.
Hence, the methods to find the square root of numbers are:
- Square Root by Prime Factorisation
- Square Root by Repeated Subtraction Method
- Square Root by Long Division Method
- Square Root by Estimation Method
Let us learn each method of square root with examples.
Square root By Prime Factorization
The square root of a perfect square number is easy to calculate using the prime factorization method. Let us solve some of the examples here:
| Number | Prime Factorization | Square Root |
| 16 | 2x2x2x2 | √16 = 2×2 = 4 |
| 144 | 2x2x2x2x3x3 | √144 = 2x2x3 = 12 |
| 169 | 13×13 | √169 = 13 |
| 256 | 256 = 2×2×2×2×2×2×2×2 | √256 = (2x2x2x2) = 16 |
| 576 | 576 = 2x2x2x2x2x2x3x3 | √576 = 2x2x2x3 = 24 |
Finding Square Roots by Repeated Subtraction Method
As per the repeated subtraction method, if a number is a perfect square, then we can determine its square root by:
- Repeatedly subtracting consecutive odd numbers from it
- Subtract till the difference is zero
- Number of times we subtract is the required square root
For example, let us find the square root of 25.
- 25 – 1 = 24
- 24 – 3 = 21
- 21 – 5 = 16
- 16 – 7 = 9
- 9 – 9 = 0
Since, the subtraction is done for 5 times, hence the square root of 25 is 5.
Finding Square Roots by Long Division Method
Finding square roots for the imperfect numbers is a bit difficult but we can calculate using a long division method. This can be understood with the help of the example given below. Consider an example of finding the square root of 436.
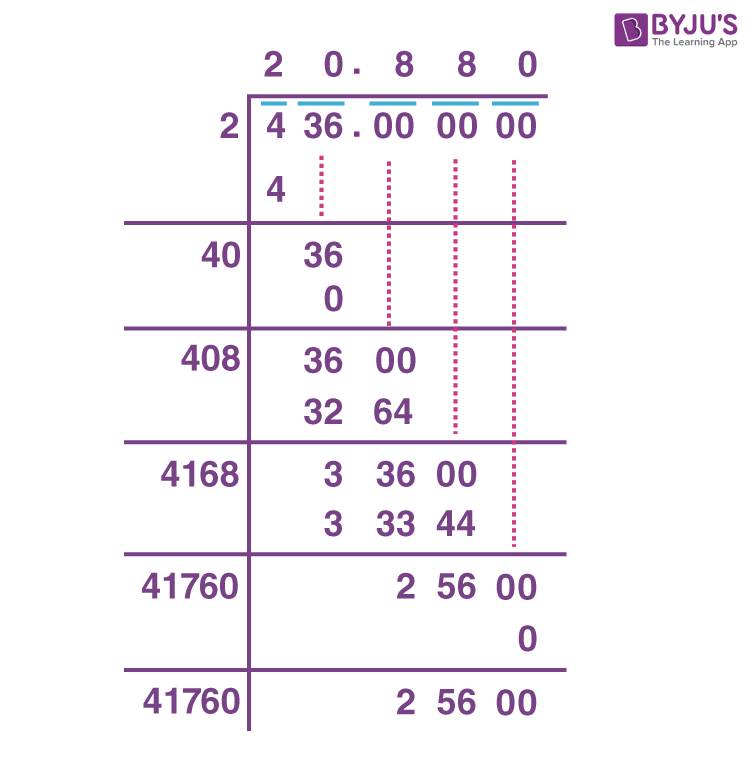
Thus, the square root of 436 is 20.880 (rounding to 3 decimals).
Square root by Estimation Method
This method is used as an approximation method, to find the square root by guessing the values.
For example, the square root of 4 is 2 and the square root of 9 is 3, thus, we can guess the square root of 5 will lie between 2 and 3.
But, we need to check the value of √5 is nearer to 2 or 3. Let us find the square of 2.2 and 2.8.
- 2.22 = 4.84
- 2.82 = 7.84
Since the square of 2.2 gives an approximate value of 5, thus we can estimate the square root of 5 is equal to 2.2 approximately.
How to Find Square Roots Without Calculator?
This is quite an interesting way to figure out the square root of a given number. The procedure is completely based on the method called “guess and check”. Guess your answer, and verify. Repeat the procedure until you have the desired accurate result. We can also use the long division method to find the square root of a number.
Square Root of Perfect squares
Below are the numbers which are perfect squares and then finding the square roots of such numbers is easy.
- 12 = 1 ⇔ √1 = 1
- 22 = 4 ⇔ √4 = 2
- 32 = 9 ⇔ √9 = 3
- 42 = 16 ⇔ √16 = 4
- 52 = 25 ⇔ √25 = 5
- 62 = 36 ⇔ √36 = 6
- 72 = 49 ⇔ √49 = 7
- 82 = 64 ⇔ √64 = 8
- 92 = 81 ⇔ √81 = 9
- 102 = 100 ⇔ √100 = 10
Hence, 1, 4, 9, 16, 25, 36, 49, 64, 81 and 100 are the perfect squares here. Check square roots of some numbers here:
Square Root Table (1 to 50)
Here is the list of the square root of numbers from 1 to 50.
| √n | Value | √n | Value | √n | Value |
| √1 | 1 | √18 | 4.2426 | √35 | 5.9161 |
| √2 | 1.4142 | √19 | 4.3589 | √36 | 6 |
| √3 | 1.7321 | √20 | 4.4721 | √37 | 6.0828 |
| √4 | 2 | √21 | 4.5826 | √38 | 6.1644 |
| √5 | 2.2361 | √22 | 4.6904 | √39 | 6.2450 |
| √6 | 2.4495 | √23 | 4.7958 | √40 | 6.3246 |
| √7 | 2.6458 | √24 | 4.8990 | √41 | 6.4031 |
| √8 | 2.8284 | √25 | 5 | √42 | 6.4807 |
| √9 | 3 | √26 | 5.0990 | √43 | 6.5574 |
| √10 | 3.1623 | √27 | 5.1962 | √44 | 6.6332 |
| √11 | 3.3166 | √28 | 5.2915 | √45 | 6.7082 |
| √12 | 3.4641 | √29 | 5.3852 | √46 | 6.7823 |
| √13 | 3.6056 | √30 | 5.4772 | √47 | 6.8557 |
| √14 | 3.7417 | √31 | 5.5678 | √48 | 6.9282 |
| √15 | 3.8730 | √32 | 5.6569 | √49 | 7 |
| √16 | 4 | √33 | 5.7446 | √50 | 7.0711 |
| √17 | 4.1231 | √34 | 5.8310 |
Square Root of Decimal
A decimal value will have a dot (.) such as 3.8, 5.2, 6.33, etc. For a whole number, we have understood how to derive the square root but let us see how to get the square root of a decimal.
| Example: Find the square root of 0.09.Let N2 = 0.09
Taking root on both sides. N = ±√0.09 As we know, 0.3 x 0.3 = (0.3)2 = 0.09 Therefore, N = ±√(0.3)2 N = ±(0.3) |
Square Root of Negative Number
The square root of a negative number is not a real number but a complex number. It is because the square of any integer is a positive value. The square root of a negative number, say, -y, is: √(-y)= i√y, where ‘i’ is the square root of -1.
Square root of Complex Numbers
To find the square root of complex numbers is a little complicated. We can find the square root of a+ib using the below formula:
where a+ib is a complex number.
How to Solve the Square Root Equation?
A square root equation is such an equation that has a variable in the radicand of the root. It is also called the radical equation.
To solve the radical equation, we need to follow the below steps:
- Isolate the square root to one of the sides (L.H.S or R.H.S).
- Square both the sides of the given equation
- Now solve the rest equation.
Let us understand the steps with examples.
| Example: Solve the radical equation √(4a+9) – 5 = 0Solution: Given, √(4a+9) – 5 = 0
Isolate the square root term first. Then the equation becomes, √(4a+9) = 5 Now on squaring both the sides, we get; 4a+9 = 52 4a = 16 a = 16/4 a = 4 |
Condition 1: If the equation has more than one radical or square root.
If the radical equation has more than one root then repeat the above given steps for each square root.
| Example: Solve √(2x−5) − √(x−1) = 1Let us isolate one of the square root.
√(2x−5) = 1 + √(x−1) Now squaring both the sides 2x – 5 = (1 + √(x−1))2 Apply the algebraic identity, (a+b)2 = a2 + b2 + 2ab. 2x−5 = 1 + 2√(x−1) + (x−1) 2x−5 = 2√(x−1) + x x−5 = 2√(x−1) Now again isolate the square root. √(x−1) = (x−5)/2 x−1 = ((x−5)/2)2 x−1 = (x2 − 10x + 25)/4 4x−4 = x2 − 10x + 25 4x − 4 − x2 + 10x − 25 = 0 −x2 + 14x − 29 = 0 x2 − 14x + 29 = 0 Using the quadratic formula, we can solve the above equation. x = 2.53 and x = 11.47 |
Squaring a Number
To find the square of a number, we need to multiply the number by itself.
For example, 2 multiplied by 2 is equal to 4
Below is a 2 by 2 table that shows, a total of four blocks.
| 1 | 2 |
| 3 | 4 |
Similarly,
square of 5 is: 5 multiplied by 5 = 5 x 5 = 52 = 25
Square of 9 = 92 = 9 x 9 = 81
Square of 15 = 152 = 15 x 15 = 225
Applications of Square Roots
The square root formula is an important section of mathematics that deals with many practical applications of mathematics and it also has its applications in other fields such as computing. Some of the applications are:
- Quadratic equations
- Algebra
- Geometry
- Calculus
List of Square Roots of Numbers
Video Lessons on Square Roots
Visualising square roots

Finding Square roots

Solved Examples on Square Roots
Let us understand this concept with the help of an example:
Example 1: Solve √10 to 2 decimal places.
Solution:
Step 1: Select any two perfect square roots that you feel your number may fall in between.
We know that 22 = 4; 32 = 9, 42 = 16 and 52 = 25
Now, choose 3 and 4 (as √10 lies between these two numbers)
Step 2: Divide the given number by one of those selected square roots.
Divide 10 by 3.
=> 10/3 = 3.33 (round off answer at 2 places)
Step 3: Find the average of root and the result from the above step i.e.
(3 + 3.33)/2 = 3.1667
Verify: 3.1667 x 3.1667 = 10.0279 (Not required)
Repeat step 2 and step 3
Now 10/3.1667 = 3.1579
Average of 3.1667 and 3.1579.
(3.1667+3.1579)/2 = 3.1623
Verify: 3.1623 x 3.1623 = 10.0001 (more accurate)
Stop the process.
Example 2: Find the square roots of whole numbers which are perfect squares from 1 to 100.
Solution: The perfect squares from 1 to 100: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100
| Square root | Result |
| √1 | 1 |
| √4 | 2 |
| √9 | 3 |
| √16 | 4 |
| √25 | 5 |
| √36 | 6 |
| √49 | 7 |
| √64 | 8 |
| √81 | 9 |
| √100 | 10 |
Example 3: What is:
- The square root of 2
- The square root of 3
- The square root of 4
- The square root of 5
Solution: Use square root list, we have
- value of root 2 i.e. √2 = 1.4142
- value of root 3 i.e. √3 = 1.7321
- value of root 4 i.e. √4 = 2
- value of root 5 i.e. √5 = 2.2361
Example 4: Is square Root of a Negative Number a whole number?
Solution: No, As per the square root definition, negative numbers shouldn’t have a square root. This is because if we
multiply two negative numbers, the result will always be a positive number. Square roots of negative numbers expressed
as multiples of i (imaginary numbers).
Example 5: Solve the equation: √(x+2) = 4
Solution: Given,
√(x+2) = 4
Squaring both the sides, we get;
x+2 = √4
x+2 = ±4
x = ±4 – 2
Therefore,
Practice Questions on Square roots
- What is square root of 64?
- Simplify √142
- Find the square root of 250
- What is the square root of 10000?
- Find the value of √12.
- Are √155, √121 and √139 perfect squares?
To learn more about square roots and other Maths topics in a more engaging and effective way, register with BYJU’S – The Learning App.


This app is very helpful
I appreciate it
Very nice because it helps me doing my homework of mathematics
Very good app