In 3D geometry, position vectors are used to denote the position or location of a point with respect to the origin. The plane, as we know, is a 3D object formed by stacks of lines kept side by side. A 3D space can have an infinite number of planes aligned to one another at an infinite number of angles. In this article, we will derive a general formula for the calculation of angle between two planes in the 3D space.
How to Calculate the Angle Between Two Planes?
The angle between two planes is generally calculated with the knowledge of angle between their normal. In other words, the angle between normal to two planes is the angle between the two planes. This can be understood quite clearly from the below figure:
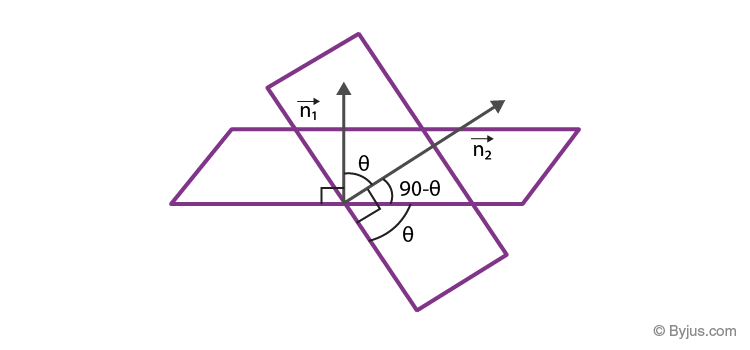
Let
From the above figure, we learnt that the angle between the two planes is equal to the angle between their normal, thus,
![]()
Calculation of Angle Between Two plane in the Cartesian Plane
Let A1 x + B1 y + C1z + D1 = 0 and A2x + B2y + C2 z + D2 = 0 be the equation of two planes aligned to each other at an angle θ where A1, B1, C1 and A2, B2, C2 are the direction ratios of the normal to the planes, then the cosine of the angle between the two planes is given by:

Angle Between Two Planes Example
Question: Calculate the angle between the two planes given by the equation 2x + 4y – 2z = 5 and 6x – 8y – 2z = 14.
Solution: As mentioned above, the angle between two planes is equal to the angle between their normals. Normal vectors to the above planes are represented by:
![]()

To learn about other techniques to calculate the angle between two planes, download BYJU’S – The Learning App.

Comments