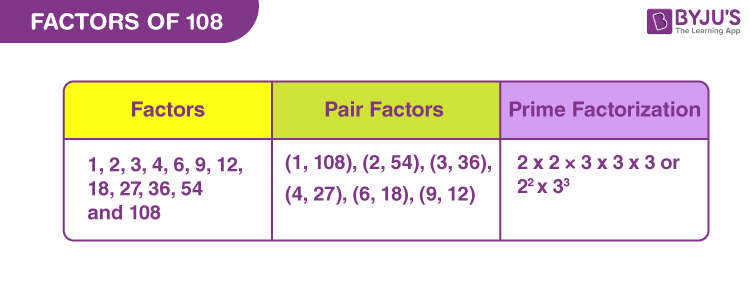
The factors of 108 are the numbers that are multiplied in pairs resulting in an original number. For example, the factors of 108 can be positive or negative. Similarly, the pair factors of 108 can also be represented in the positive as well as in the negative pair. For example, the factor pair of 108 can be (1, 108) or (-1, -108). If we multiply the pair of negative factors, such as multiplying -1 and -108 results in 108. In this article, we are going to learn the factors of 108 and also get to know about the positive and negative pair factors of 108, and the prime factorization of 108 and many solved examples.
Table of Contents:
- What are the Factors of 108?
- Pair Factors of 108
- Factors of 108 by Division Method
- Prime Factorization of 108
- Solved Examples
- FAQs
What are the Factors of 108?
The factors of 108 are the numbers that divide 108 exactly without leaving a remainder. As the number 108 is an even composite number, it has many factors other than 1 and 108. Hence, the factors of 108 are 1, 2, 3 , 4, 6, 9, 12, 18, 27, 36, 54, and 108. Similarly, the negative factors of 108 are -1, -2, -3 , -4, -6, -9, -12, -18, -27, -36, -54, and -108.
|
Factors of 108: 1, 2, 3 , 4, 6, 9, 12, 18, 27, 36, 54, and 108. Prime Factorization of 108: 2 × 2 × 3 × 3 × 3 or 22 × 33. |
Pair Factors of 108
A pair of numbers that are multiplied together resulting in an original number 108 is called the pair factors of 108. As discussed earlier, the pair factors of 108 can be represented in positive as well as in negative form. Thus, the positive and negative pair factors of 108 are given below:
Positive Pair Factors of 108:
|
Positive Factors of 108 |
Positive Pair Factors of 108 |
|
1×108 |
(1, 108) |
|
2×54 |
(2, 54) |
|
3×36 |
(3, 36) |
|
4×27 |
(4, 27) |
|
6×18 |
(6, 18) |
|
9×12 |
(9, 12) |
Negative Pair Factors of 108:
|
Negative Factors of 108 |
Negative Pair Factors of 108 |
|
-1×-108 |
(-1, -108) |
|
-2×-54 |
(-2, -54) |
|
-3×-36 |
(-3, -36) |
|
-4×-27 |
(-4, -27) |
|
-6×-18 |
(-6, -18) |
|
-9×-12 |
(-9, -12) |
Factors of 108 by Division Method
In the division method, the factors of 108 are found by dividing 108 by different consecutive integers. If the integers divide 108 exactly and leave the remainder 0, then the integers are the factors of 108. Here, we will discuss how to find the factors of 108 using the division method.
- 108/1 = 108 (Factor = 1 and Remainder = 0)
- 108/2 = 54 (Factor = 2 and Remainder = 0)
- 108/3 = 36 (Factor = 3 and Remainder = 0)
- 108/4 = 27 (Factor = 4 and Remainder = 0)
- 108/6 = 18 (Factor = 6 and Remainder = 0)
- 108/9 = 12 (Factor = 9 and Remainder = 0)
- 108/12 = 9 (Factor = 12 and Remainder = 0)
- 108/18 = 6 (Factor = 18 and Remainder = 0)
- 108/27 = 4 (Factor = 27 and Remainder = 0)
- 108/36 = 3 (Factor = 36 and Remainder = 0)
- 108/54 = 2 (Factor = 54 and Remainder = 0)
- 108/108 = 1 (Factor = 108 and Remainder = 0)
If we divide 108 by any numbers other than 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, and 108, it leaves a remainder. Hence, the factors of 108 are 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, and 108.
Prime Factorization of 108
In the prime factorization of 108, the number 108 is written as the product of its prime factors. Now, let us discuss how to find the prime factors of 108.
Step 1: Write down the pair factor of 108, say (1, 108)
Step 2: Check whether the numbers in the pair factors are composite or prime numbers.
In the factor pair (1, 108), leave the number 1 as it cannot be factored further.
Now, let us take the other number 108. As the number 108 is an even composite number, it can be further split into its prime factors. Hence, the number 108 is written as the product of 4 and 27.
Also, 4 is further factored as the product of 2 and 2 and 27 is further factored as the product of 3, 3 and 3.
Hence, 108 = 2 × 2 × 3 × 3 × 3.
Thus, the prime factorization of 108 is 2 × 2 × 3 × 3 × 3 or 22 × 33.
| Learn more on Factors | |
| Factors of 15 | Factors of 12 |
| Factors of 72 | Factors of 48 |
Examples
Example 1:
Find the common factors of 108 and 107.
Solution:
The factors of 108 are 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, and 108.
The factors of 107 are 1 and 107.
As 107 is a prime number, the common factor of 108 and 107 is 1.
Example 2:
Find the common factors of 108 and 109.
Solution:
Factors of 108 = 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, and 108.
Factors of 109 = 1 and 109.
As 109 is a prime number, the common factor of 108 and 109 is 1 only.
Example 3:
Find the common factors of 108 and 54.
Solution:
The factors of 108 are 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, and 108.
The factors of 54 are 1, 2, 3, 6, 9, 18, 27 and 54.
Hence, the common factors of 108 and 54 are 1, 2, 3, 6, 9, 18, 27 and 54.
Register at BYJU’S to know about the factors of other numbers and mathematical concepts in a fun and engaging way.
Frequently Asked Questions on Factors of 108
What are the factors of 108?
The factors of 108 are 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, and 108.
What is the prime factorization of 108?
The prime factorization of 108 is 2 × 2 × 3 × 3 × 3 or 22 × 33.
What are the positive pair factors of 108?
The positive pair factors of 108 are (1, 108), (2, 54), (3, 36), (4, 27), (6, 18) and (9, 12).
Write down the negative pair factors of 108.
The positive pair factors of 108 are (-1, -108), (-2, -54), (-3, -36), (-4, -27), (-6, -18) and (-9, -12).
Is 27 a factor of 108?
Yes, 27 is a factor of 108. As 27 divides 108 exactly and leaves the remainder 0, 27 is a factor of 108.
