In Mathematics, Laurent’s series expansion is considered to be an essential tool in complex analysis. Laurent’s series helps us to work around the singularities of the complex function. In this article, let us discuss the definition, formulas, difference between the Taylor series and Laurent’s series with solved examples in detail.
Table of Contents:
What is Laurent’s Series?
Laurent’s series, also known as Laurent’s expansion, of a complex function f(z) is defined as a representation of that function in terms of power series that includes the terms of negative degree. Laurent’s series was first published by Pierre Alphonse Laurent in 1843.
Laurent’s Series Formula
Assume that f(z) is analytic on the annulus (i.e.,) A: r1 < | z- z0| < r2, then f(z) is expressed in terms of series is:
Here the coefficients an and bn have the following formulas:
Here,
γ can be any circle | w – z0| = r, inside the annulus. It means, r1 < r < r2.
From the series, we can also say,
- \(\begin{array}{l}\sum_{n=0}^{\infty }a_{n}(z-z_{0})^{n} \text{ converges to the analytic function, when} |z-z_{0}| < r_{2}.\end{array} \)
- \(\begin{array}{l}\sum_{n=1}^{\infty }\frac{b_{n}}{(z-z_{0})^{n}}\text{ converges to the analytic function, when} |z-z_{0}| > r_{1}.\end{array} \)
Thus, together both series converges on the annulus (A), where f is analytic.
Thus, the entire series
Whereas, the series
Similarly,
Note: It should be noted that as f(z) may not be analytic (even defined) at z0, there exists no such formulas for the coefficients using derivatives.
The below diagram represents the contour used to prove the formulas of Laurent’s series:
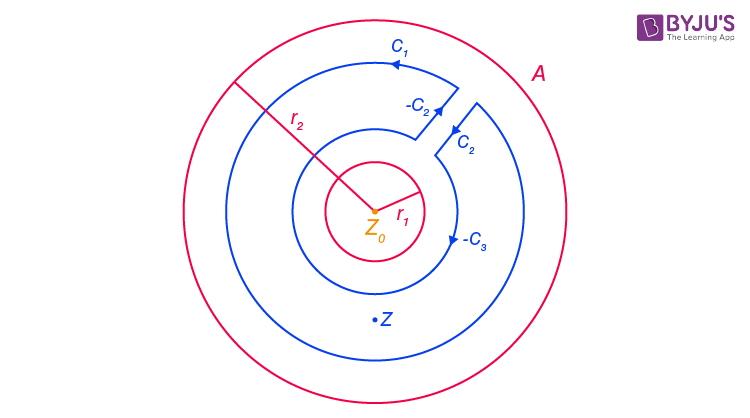
Laurent’s Series Convergence
The Laurent’s series converges on the open annulus A ≡ {z : r1 < |z − z0| < r2}. In other words, the Laurent series converges, when both the positive and negative degree of the power series converges. Also, the Laurent series convergence should be uniform for compact sets. Hence, we can say that the convergent series will define the holomorphic function on open annulus.
| Also, read: |
Difference Between Taylor and Laurent Series
The following are the major differences between Taylor and Laurent Series:
| S. No | Laurent’s Series | Taylor’s Series |
| 1 | Laurent series is defined as a power series, where it contains negative power terms. | Taylor’s series is also a power series where it does not contain negative power terms. |
| 2 | If a function f(z) is not analytic at a point, but the function is analytic around the neighbourhood, then it can be expanded using Laurent’s series. | If a function f(z) is analytic at a point, it can be expanded using Taylor’s series. |
Laurent Series Solved Examples
Example 1:
Determine the Laurent series for the function, f(z) = (z+1)/z around z0 = 0. Also, define the region where the function is valid.
Solution:
Given function, f(z) = (z+1)/z
The given function can be written as:
f(z) = (z/z) + (1/z)
f(z) = 1+(1/z)
Hence, f(z) = 1+ (1/z) is the Laurent series, which is valid on the infinite region 0 < |z| < ∞.
Example 2:
Compute the Laurent series for the function f(z) = z / [z2 + 1] around z0 = i. Give the region where the function is valid. Also, determine the principal part of the Laurent series.
Solution:
Given: f(z) = z / [z2 + 1]
Using the partial fraction, the above function can be written as:
As 1/(z+i) is analytic at z = i, it should have Taylor expansion and it can be found using the geometric series.
Therefore, the Laurent series is
As we know, the principal part is given by the first term.
And, the region of convergence is 0 < |z − i| < 2.
Note: The function f(z) on the region 2 < |z − i| < ∞ will produce a different Laurent series.
Frequently Asked Questions on Laurent’s Series
What is Laurent’s Series?
Laurent’s Series is used to express the complex function when the Taylor series cannot be applied. Laurent’s series can be used if a function f(z) is not analytic at a point, but the function is analytic around neighbourhood.
Are Laurent’s series and Taylor’s series the same?
The power series which consists of only positive power terms is called the Taylor series, whereas the power series containing the negative power terms is called Laurent’s series.
Which portion is considered to be the principal part of Laurent’s series?
In Laurent’s series, the portion that consists of terms with the negative degree is called the singular or the principal part of Laurent’s series.
Comments