Trigonometry is one of the branches of mathematics. There are six trigonometric functions and the limit of each of these functions leading to the point. However, we can calculate the limits of these functions according to the continuity of the function, considering the domain and range of trigonometric functions. This can be observed in the graph of every trigonometric function given below, as the limit of each function is different at the same point.
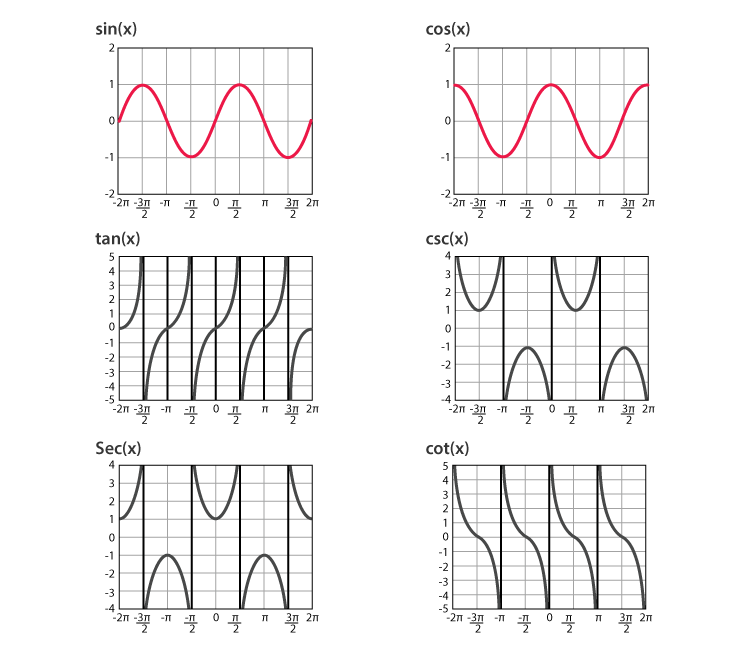
These graphs are used to determine the limits of given trigonometry functions for general values of x.
Get more information on trigonometry graphs here.
Limits of Trigonometric Functions Formulas
Suppose a is any number in the general domain of the corresponding trigonometric function, then we can define the following limits.
| Function | Limit of the function |
| sin x | \(\begin{array}{l}\lim_{x\rightarrow a}sin\ x = sin\ a\end{array} \) |
| cos x | \(\begin{array}{l}\lim_{x\rightarrow a}cos\ x = cos\ a\end{array} \) |
| tan x | \(\begin{array}{l}\lim_{x\rightarrow a}tan\ x = tan\ a\end{array} \) |
| cosec x | \(\begin{array}{l}\lim_{x\rightarrow a}cosec\ x = cosec\ a\end{array} \) |
| sec x | \(\begin{array}{l}\lim_{x\rightarrow a}sec\ x = sec\ a\end{array} \) |
| cot x | \(\begin{array}{l}\lim_{x\rightarrow a}cot\ x = cot\ a\end{array} \) |
We know that the graphs of the functions y = sin x and y = cos x approach different values between -1 and 1 as shown in the above figure. Thus, the function is oscillating between the values, so it will be impossible for us to find the limit of y = sin x and y = cos x as x tends to ±∞. Therefore, the limits of all six trigonometric functions when x tends to ±∞ are tabulated below:
| Function | Limit of the function for ±∞ |
| sin x | \(\begin{array}{l}\lim_{x \rightarrow \pm \infty} \sin\ x=not\ defined\end{array} \) |
| cos x | \(\begin{array}{l}\lim_{x \rightarrow \pm \infty} \cos\ x=not\ defined\end{array} \) |
| tan x | \(\begin{array}{l}\lim_{x \rightarrow \pm \infty} \tan\ x=not\ defined\end{array} \) |
| cosec x | \(\begin{array}{l}\lim_{x \rightarrow \pm \infty}\ cosec\ x=not\ defined\end{array} \) |
| sec x | \(\begin{array}{l}\lim_{x \rightarrow \pm \infty} \sec\ x=not\ defined\end{array} \) |
| cot x | \(\begin{array}{l}\lim_{x \rightarrow \pm \infty} \cot\ x=not\ defined\end{array} \) |
Apart from the above formulas, we can define the following theorems that come in handy in calculating limits of some trigonometric functions.
Theorem 1:
Let f and g be two real valued functions with the same domain such that
f(x) ≤ g(x) for all x in the domain of definition, For some a, if both
Theorem 2:
Let f, g and h be real functions such that f(x) ≤ g( x) ≤ h(x) for all x in the common domain of definition. For some real number a, if
This is also known as Sandwich theorem or Squeeze theorem.
Based on this, we can write the following two important limits.
(i)
(ii)
Using these identities we can solve complex limits problems that involve trigonometric functions.
Now, go through the examples of limits of trigonometric functions along with solutions to understand the concept easily.
Video Lesson on Trigonometry

| Also, read: |
Limits of Trigonometric Functions Examples
Example 1:
Evaluate:
Solution:
Multiplying and dividing the function by “ax”,
Now, take the constant term out of the limit.
As we know,
So, replacing “x” with “ax”,
Therefore,
Example 2:
Find the value of
Solution:
We know that,
and
Now,
= cos π/ (sin π/2)
= -1/1
= -1
Therefore,

Comments