In mathematics, the logarithm table is used to find the value of the logarithmic function. The simplest way to find the value of the given logarithmic function is by using the log table. Learn Mathematics at BYJU’S in an easy way.
Here, the definition of the logarithmic function and procedure to use the logarithm table is given in detail. Also, get Antilogarithm table here for reference.
Table of Contents:
Logarithmic Function Definition
The logarithmic function is defined as an inverse function to exponentiation. The logarithmic function is stated as follows
For x, a > 0, and a≠1,
y= loga x, if x = ay
Then the logarithmic function is written as:
f(x) = loga x
The most common bases used in logarithmic functions are base e and base 10. The log function with base 10 is called the common logarithmic function and it is denoted by log10 or simply log.
f(x) = log10
The log function to the base e is called the natural logarithmic function and it is denoted by loge.
f(x) = loge x
To find the logarithm of a number, we can use the logarithm table instead of using a mere calculation. Before finding the logarithm of a number, we should know about the characteristic part and mantissa part of a given number
- Characteristic Part – The whole part of a number is called the characteristic part. The characteristic of any number greater than one is positive, and if it is one less than the number of digits to the left of the decimal point in a given number. If the number is less than one, the characteristic is negative and is one more than the number of zeros to the right of the decimal point.
- Mantissa Part – The decimal part of the logarithm number is said to be the mantissa part and it should always be a positive value. If the mantissa part is in a negative value, then convert into the positive value.
How to Use the Log Table?
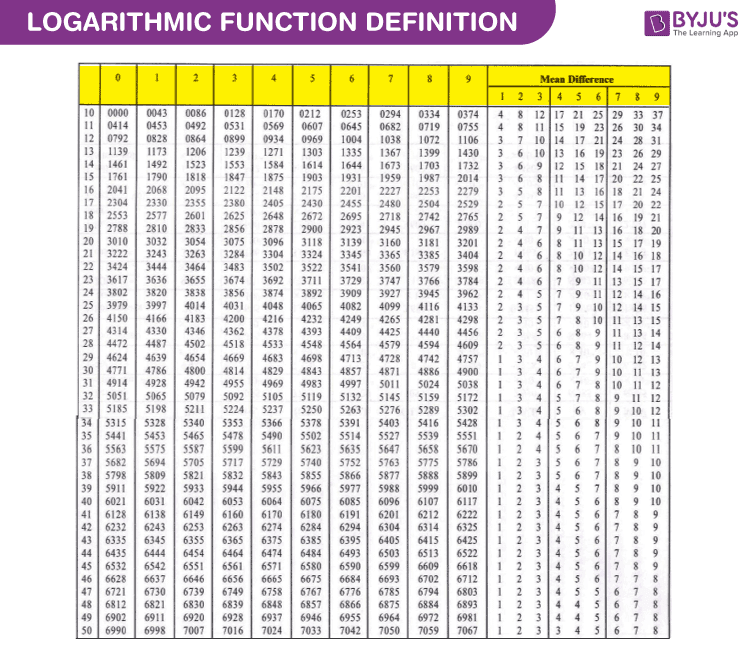
The procedure is given below to find the log value of a number using the log table. First, you have to know how to use the log table. The log table is given for the reference to find the values.
Step 1: Understand the concept of the logarithm. Each log table is only usable with a certain base. The most common type of logarithm table is used is log base 10.
Step 2: Identify the characteristic part and mantissa part of the given number. For example, if you want to find the value of log10 (15.27), first separate the characteristic part and the mantissa part.
Characteristic Part = 15
Mantissa part = 27
Step 3: Use a common log table. Now, use row number 15 and check column number 2 and write the corresponding value. So the value obtained is 1818.
Step 4: Use the logarithm table with a mean difference. Slide your finger in the mean difference column number 7 and row number 15, and write down the corresponding value as 20.

Step 5: Add both the values obtained in step 3 and step 4. That is 1818+20= 1838. Therefore, the value 1838 is the mantissa part.

Step 6: Find the characteristic part. Since the number lies between 10 and 100, (101 and 102), the characteristic part should be 1.
Step 7: Finally combine both the characteristic part and the mantissa part, it becomes 1.1838.
Sample Examples
Here the sample example to find the value of the logarithmic function using the logarithm table is given.
Example 1:
Find the value of log10 2.872
Solution:
Step 1: Characteristic Part= 2 and mantissa part= 872
Step 2: Check the row number 28 and column number 7. So the value obtained is 4579.
Step 3: Check the mean difference value for row number 28 and mean difference in column 2. The value corresponding to the row and column is 3
Step 4: Add the values obtained in step 2 and 3, we get 4582. This is the mantissa part.
Step 5: Since the number of digits to the left side of the decimal part is 1, the characteristic part is less than 1. So the characteristic part is 0
Step 6: Finally combine the characteristic part and the mantissa part. So it becomes 0.4582.
Therefore, the value of log 2.872 is 0.4582.
Example 2:
Find the value of log10 (∛2.134)
Solution:
We know by the property of logarithms,
loga bn = n loga b
Thus, log10 (∛2.134) = 1/3 log10 2.134
Now we calculate log10 2.134
For the mantissa, check row 21 and column 3 in the logarithm table, which is 3284. Now check the mean difference 4 of the same row, which is 8.
∴ Mantissa is 3284 + 8 = 3292
For the characteristic part, since there is only 1 digit in the left side of decimal, hence characteristic is 0
∴ log10 2.134 = 0.3292
Then, log10 (∛2.134) = 1/3 log10 2.134 = 1/3 × 0.3292 = 0.10973.
Note: To find the value of ∛2.134, we just have to find the antilogarithm of 0.10973.
Practice Questions
- Find the value of log10 23.46.
- Find the value of log10 345.
- Find the value of log10 25.
| Related Links | |
| Exponential Function | Logarithm Formula |
| Log Base 2 | Logarithms |
Register with BYJU’S to know more about the usage of logarithm table and antilog table and also watch interactive videos to learn with ease.
Frequently Asked Questions on Logarithm Table
What is the base of the common logarithm?
How find the logarithm of a given number?
Calculate the characteristic, which is determined by the whole number part of the given number.
Calculate the mantissa, which is determined by the significant digits of the given number.
Finally, combine the characteristic and mantissa with a decimal point.


Ya it is good
Wow…thank you….
i’m grateful….
now i can use a log table….
Thank you I can use logarithms table am so grateful
Thank U … Yeeh! I can use log table 🙏👍👍
I’m very grateful, now I can make use of logarithm table without any problems.
Thanks for teaching me well
I’m happy
Yeah, thanks I can use logarithm tables
Very good
Well, That’s Useful.
Thanks 😉
That’s great information about log table.
I understand how to solve log table.
Thank you