In this article, the concept of the onto function, which is also called a surjective function, is discussed. Also, learn about its definition, the way to find out the number of onto functions and how to prove whether a function is surjective with the help of examples.
To recall, a function is something, which relates elements/values of one set to the elements/values of another set, in such a way that elements of the second set is identically determined by the elements of the first set. A function has many types which define the relationship between two sets in a different pattern. They are various types of functions like one to one function, onto function, many to one function, etc.
Table of Contents:
Onto Function Definition (Surjective Function)
Onto function could be explained by considering two sets, Set A and Set B, which consist of elements. If for every element of B, there is at least one or more than one element matching with A, then the function is said to be onto function or surjective function. The term for the surjective function was introduced by Nicolas Bourbaki.
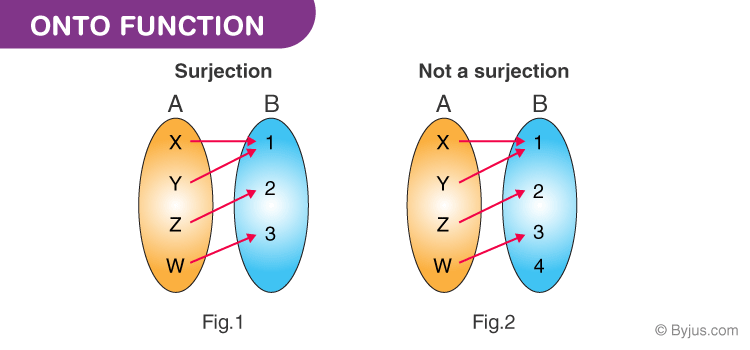
In the first figure, you can see that for each element of B, there is a pre-image or a matching element in Set A. Therefore, it is an onto function. But if you see in the second figure, one element in Set B is not mapped with any element of set A, so it’s not an onto or surjective function.
Number of Onto Functions (Surjective functions) Formula
If we have to find the number of onto function from a set A with n number of elements to set B with m number of elements.
Thus,
Total number of functions from A to B = mn
Total number of onto functions = Total number of functions – Number of functions which are not onto
The formula to find the total number of function that are not onto is given by:
Therefore, the Number of onto functions can be found using the formula,
\(\begin{array}{l}m^{n}\,-\,(^{m}_{1})(m-1)^{n}\,+\,(^{m}_{2})(m-2)^{n}\,-\,(^{m}_{3})(m-3)^{n}\,+\,.\,.\,.\,.\,. -(^{m}_{m-1})(1)^{n}\end{array} \)
|
When
n < m, the number of onto functions = 0
n = m, the number of onto functions = m!
Properties of a Surjective Function (Onto)
- We can define onto function as if any function states surjection by limit its codomain to its range.
- The domain is basically what can go into the function, codomain states possible outcomes and range denotes the actual input of the function.
- Every onto function has a right inverse.
- Every function with a right inverse is a surjective function.
- If we compose onto functions, it will result in onto function only.
Now let us take a surjective function example to understand the concept better.
Onto Function Example Questions
Example 1:
Let A = {1, 5, 8, 9) and B {2, 4} And f={(1, 2), (5, 4), (8, 2), (9, 4)}. Then prove f is a onto function.
Solution:
From the question itself we get,
A={1, 5, 8, 9)
B{2, 4}
& f={(1, 2), (5, 4), (8, 2), (9, 4)}
So, all the element on B has a domain element on A or we can say element 1 and 8 & 5 and 9 has same range 2 & 4 respectively.
Therefore, f: A → B is a surjective function.
Example 2:
Find the number of onto functions from the set X = {1, 2, 3, 4} to the set y= {a, b, c} .
Given:
Set X = {1, 2, 3, 4}
Set Y = {a, b, c}
Here, n=4 and m=3
Now, substitute the values of m and n in the formula, we get
= 34 – 3C1(2)4 + 3C2(1)4
= 81 – 3 (16) + 3(1)
= 81 – 48 + 3
= 84-48
= 36
Thus, the number of onto functions from set X to set Y is 36.
| More Articles Related to Surjective Function | |
|---|---|
| Inverse Of A Function | Composition Of Functions & Inverse Of A Function |
| Greatest Integer Function | Relations And Its Types |
To learn more similar maths concepts in a more engaging and effective way, keep visiting BYJU’S and download BYJU’S app for experiencing a personalized and interactive learning experience.
Frequently Asked Questions on Onto Function
What is meant by onto function?
If A and B are the two sets, if for every element of B, there is at least one or more element matching with set A, it is called the onto function.
What is the other name of the onto function?
The onto function is also called the surjective function.
How to determine if a graph is onto?
The function “f” is onto, if and only if its graph function intersects the horizontal line at least once.
What can we call if a function is both injective and surjective?
If a function is both injective and surjective, then the function is called the bijective function, which is also called the one-to-one correspondence.
Mention two properties of the surjective function.
Every onto function has a right inverse
In the surjective function, the range of the function “f” is equal to the codomain.


Comments