Telangana 10th Annual Exam Question Papers 2019 Maths Paper 1 with Solutions – Free Download
Telangana SSC Class 10 Maths 2019 Question Paper 1 with solutions is given at BYJU’S, which will help the students in verifying their answers after practising Telangana 10th Maths question papers. Students can get the solutions for all recent year question papers of Class 10 at BYJU’S. Telangana board conducts SSC Maths exam with two papers, each having part A and part B, students can download and practice the pdf of Telangana SSC Board (TS SSC) Question Paper 1 for Class 10th Maths 2019 to improve their problem-solving skills and for the better understanding of exam pattern.
Download TS SSC 2019 Maths Question Paper 1
Download TS SSC 2019 Maths Question Paper 1 With Solutions
Telangana Board SSC Class 10 Maths 2019 Question Paper 1 with Solutions
PART A
SECTION – I
1. If A = {x: x is a factor of 24}, then find n(A).
Solution:
A = {1, 2, 3, 4, 6, 8, 12, 24}
n(A) = 8
2. Find the HCF of 24 and 33 by using a division algorithm.
Solution:
24 < 33

3. Radha says “1, 1, 1,…. are in AP and also in GP”. Do you agree with Radha? Give reason.
Solution:
Given,
1, 1, 1,….
If a, b, c are in AP, then a + c = 2b
Thus, 1 + 1 = 2(1)
2 = 2
Therefore, 1, 1, 1 are in AP.
If a, b, a are in GP, then, ac = b2
(1)(1) = (1)2
1 = 1
Therefore, 1, 1, 1 are in GP.
Hence, we can say that 1,1,1 are in AP and also in GP.
4. If P(x) = x4 + 1, then find P(2) – P(-2).
Solution:
Given,
P(x) = x4 + 1
P(2) = (2)4 + 1 = 16 + 1 = 17
P(-2) = (-2)4 + 1 = 16 + 1 = 17
P(2) – P(-2) = 17 – 17 = 0
5. Find the roots of the quadratic equation x2 + 2x – 3 = 0.
Solution:
Given quadratic equation is: x2 + 2x – 3 = 0
x2 + 3x – x – 3 = 0
x(x + 3) – 1(x + 3) = 0
(x – 1)(x + 3) = 0
x – 1 = 0, x + 3 = 0
x = 1, x = -3
Hence, the roots of the given quadratic equation are 1 and -3.
6. Find the centroid of ΔPQR, whose vertices are P(1, 1), Q(2, 2), R(-3, -3).
Solution:
Let the given vertices of a triangle PQR are:
(x1, y1) = (1, 1)
(x2, y2) = (2, 2)
(x3, y3) = (-3, -3)
Centroid of a triangle = [(x1 + x2 + x3)/3, (y1 + y2 + y3)/3]
= [(1 + 2 – 3)/3, (1 + 2 – 3)/3]
= (0/3, 0/3)
= (0, 0)
7. For what value of ‘t’ the following pair of linear equations has a no solution?
2x – ty = 5 and 3x + 2y = 11
Solution:
Given pair of linear equations are:
2x – ty = 5
3x + 2y = 11
Comparing with the standard form,
a1 = 2, b1 = -t, c1 = -5
a2 = 3, b2 = 2, c2 = -11
Condition for no solution of linear equations is
a1/a2 = b1/b2 ≠ c1/c2
⅔ = -t/2
⇒ t = -4/3
SECTION – II
8. If µ = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, A = {2, 3, 5, 8} and B = {0, 3, 5, 7, 10}. Then represent A ⋂ B in the Venn diagram.
Solution:
Given,
µ = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {2, 3, 5, 8}
B = {0, 3, 5, 7, 10}
A ⋂ B = {2, 3, 5, 8} ⋂ {0, 3, 5, 7, 10} = {3, 5}

9. Akhila says, “points A(1, 3), B(2, 2), C(5, 1) are collinear”. Do you agree with Akhila? Why?
Solution:
Given points are A(1, 3), B(2, 2) and C(5, 1).
If (x1, y1), (x2, y2) and (x3, y3) are collinear, then area of triangle = 0
i.e. ½ [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)] = 0
= ½ [1(2 – 1) + 2(1 – 3) + 5(3 – 2)]
= 1 + 2(-2) + 5(1)
= 1 – 4 + 5
= 2 ≠ 0
Thus, the given points are not collinear.
Hence, we do not agree with Akhila.
10. Write the quadratic equation, whose roots are 2 + √3 and 2 – √3.
Solution:
Let α and β be the roots of the quadratic equation.
Given,
2 + √3 and 2 – √3 are the roots of the quadratic equation.
Sum of the roots = α + β = 2 + √3 + 2 – √3 = 4
Product of the roots = αβ = (2 + √3)(2 – √3)
= (2)2 – (√3)2
= 4 – 3
= 1
Hence, the quadratic equation is x2 – (α + β)x + αβ = 0
x2 – 4x + 1 = 0
11. Divide x3 – 4x2 + 5x – 2 by x – 2.
Solution:

Quotient = q(x) = x2 – 2x + 1
12. Write the formula of the nth term of GP and explain the terms in it.
Solution:
The formula for nth term of GP is
an = arn – 1
Here,
an = nth term of the sequence
a = first term
r = common ratio
13. Solve the pair of linear equations 2x + 3y = 8 and x + 2y = 5 by elimination method.
Solution:
Given,
2x + 3y = 8….(i)
x + 2y = 5….(ii)
(ii) × 2 – (i),
2x + 4y – (2x + 3y) = 10 – 8
y = 2
Substituting y = 2 in (ii),
x + 2(2) = 5
x = 5 – 4
x = 1
SECTION – III
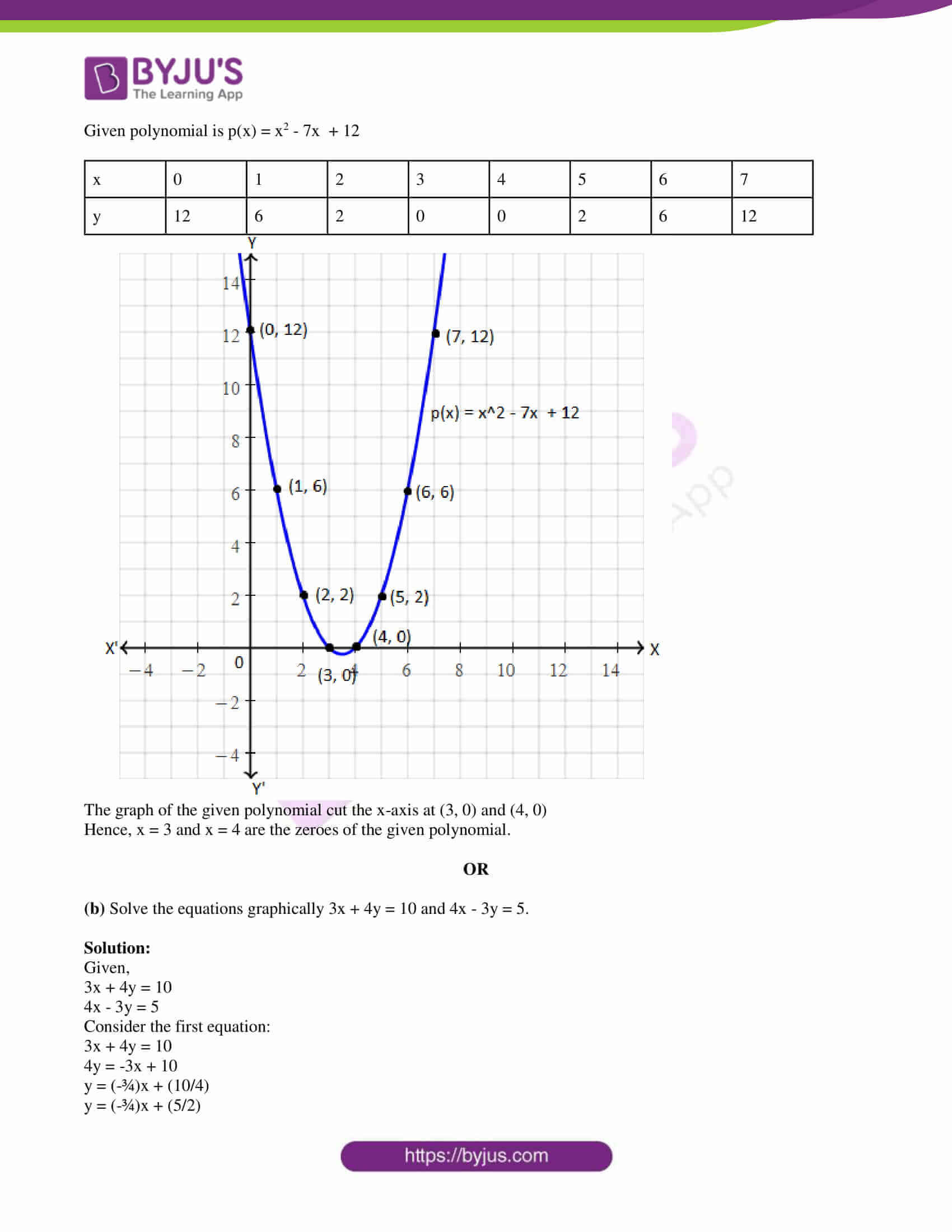
14. (a) Draw the graph of the polynomial p(x) = x2 – 7x + 12, then find its zeroes from the graph.
Solution:
Given polynomial is p(x) = x2 – 7x + 12
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 12 | 6 | 2 | 0 | 0 | 2 | 6 | 12 |

The graph of the given polynomial cut the x-axis at (3, 0) and (4, 0)
Hence, x = 3 and x = 4 are the zeroes of the given polynomial.
OR
(b) Solve the equations graphically 3x + 4y = 10 and 4x – 3y = 5.
Solution:
Given,
3x + 4y = 10
4x – 3y = 5
Consider the first equation:
3x + 4y = 10
4y = -3x + 10
y = (-¾)x + (10/4)
y = (-¾)x + (5/2)
| x | -2 | 0 | 2 | 6 |
| y | 4 | 5/2 | 1 | -2 |
Now, consider the another equation,
4x – 3y = 5
3y = 4x – 5
y = (4/3)x – (5/3)
| x | -1 | 2 | 5 | 8 |
| y | -3 | 1 | 5 | 9 |
Graph:

The lines representing the given pair of equations intersect each other at (2, 1).
Hence, the solution of a given pair of linear equations is x = 2 and y = 1.
15. (a) Find the ratio in which X-axis divides the line segment joining the points (2, -3) and (5, 6). Then find the intersection point on X-axis.
Solution:
Let P(x, 0) divide the line segment joining the points A(2, -3) and B(5, 6) in the ratio m : n.
Here,
(x1, y1) = (2, -3)
(x2, y2) = (5, 6)
Using the section formula,
P(x, 0) = [(mx2 + nx1)/ (m + n), (my2 + ny1)/ (m + n)]
(x, 0) = [ (5m + 2n)/ (m + n), (6m – 3n)/ (m + n)]
⇒ (6m – 3n)/ (m + n) = 0
⇒ 6m = 3n
⇒ m/n = 3/6
⇒ m/n = 1/2
Therefore, the required ratio is 1 : 2.
Now,
x = (5m + 2n)/ (m + n)
x = [5 + 2(2)]/ (1 + 2)
x = 9/3
x = 3
Hence, the required point on the x-axis is (3, 0).
OR
(b) Find the sum of all two digit odd multiples of 3.
Solution:
Two digit odd multiples of 3 are 15, 21, 27, 33, 39, 45, 51, 57, 63, 69, 75, 81, 87, 93, 99.
This is an AP with a = 15
Common difference = d = 6
n = 15
Sum of first n terms
Sn = n/2[2a + (n – 1)d]
S15 = (15/2) [2(15) + (15 – 1)6]
= (15/2) [30 + 14(6)]
= (15/2) [30 + 84]
= (15/2) × 114
= 855
Hence, the required sum is 855.
16. (a) If A = {x : 2x + 1, x ∈ N, x ≤ 5}, B = {x : x is a composite number, x ≤ 12}, then show that (A ⋃ B) – (A ⋂ B) = (A – B) ⋃ (B – A).
Solution:
A = {x : 2x + 1, x ∈ lN, x ≤ 5}
= {3, 5, 7, 9, 11}
B = {x : x is a composite number, x ≤ 12}
= {4, 6, 8, 9, 10, 12}
A ⋃ B = {3, 5, 7, 9, 11} ⋃ {4, 6, 8, 9, 10, 12}
= {3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
A ⋂ B = {3, 5, 7, 9, 11} ⋂ {4, 6, 8, 9, 10, 12}
= {9}
(A ⋃ B) – (A ⋂ B) = {3, 4, 5, 6, 7, 8, 9, 10, 11, 12} – {9}
= {3, 4, 5, 6, 7, 8, 10, 11, 12}
A – B = {3, 5, 7, 9, 11} – {4, 6, 8, 9, 10, 12} = {3, 5, 7, 11}
B – A = {4, 6, 8, 9, 10, 12} – {3, 5, 7, 9, 11} = {4, 6, 8, 10, 12}
(A – B) ⋃ (B – A) = {3, 5, 7, 11} ⋃ {4, 6, 8, 10, 12} = {3, 4, 5, 6, 7, 8, 10, 11, 12}
Therefore, (A ⋃ B) – (A ⋂ B) = (A – B) ⋃ (B – A)
OR
(b) Prove that √2 + √7 is an irrational number.
Solution:
Let √2 + √7 be a rational number.
√2 + √7 = a, where a is an integer.
Squaring on both sides,
(√2 + √7)2 = a2
(√2)2 + (√7)2 + 2(√2)(√7) = a2
2 + 7 + 2√14 = a2
9 + 2√14 = a2
2√14 = a2 – 9
√14 = (a2 – 9)/2
(a2 – 9)/2 is a rational number since a is an integer.
Therefore, √14 is also an integer.
We know that integers are not rational numbers.
Thus, our assumption that √2 + √7 is a rational number is wrong.
Hence, √2 + √7 is an irrational number.
17. (a) Sum of the areas of two squares is 850 m2. If the difference of their perimeters is 40 m. Find the sides of the two squares.
Solution:
Let x and y be the sides of two squares.
According to the given,
Sum of the areas of two squares = 850 m2
x2 + y2 = 850….(i)
Difference of their perimeters = 40 m
4x – 4y = 40
4(x – y) = 40
x – y = 10
x = y + 10….(ii)
Substituting (ii) in (i),
(y + 10)2 + y2 = 850
y2 + 100 + 20y + y2 – 850 = 0
2y2 + 20y – 750 = 0
2(y2 + 10y – 375) = 0
y2 + 10y – 375 = 0
y2 + 25y – 15y – 375 = 0
y(y + 25) – 15(y + 25) = 0
(y – 15)(y + 25) = 0
y – 15 = 0, y + 25 = 0
y = 15, y = -25
Measure cannot be negative.
Therefore, y = 15
Substitute y = 15 in (ii),
x = 15 + 10 = 25
Hence, the sides of two squares are 25 cm and 15 cm.
OR
(b) Sum of the present ages of two friends are 23 years, five years ago the product of their ages was 42. Find their ages 5 years hence.
Solution:
Let x and (23 – x) be the present ages (in years) of two friends.
According to the given
(x – 5)(23 – 5 – x) = 42
(x – 5)(18 – x) = 42
18x – x2 – 90 + 5x = 42
⇒ x2 – 5x – 18x + 90 + 42 = 0
⇒ x2 – 23x + 132 = 0
⇒ x2 – 11x – 12x + 132 = 0
⇒ x(x – 11) – 12(x – 11) = 0
⇒ (x – 11)(x – 12) = 0
⇒ x = 12, x = 11
If x = 12, then 23 – x = 23 – 12 = 11
If x = 11, then 23 – x = 23 – 11 = 12
Therefore, the present ages of two friends are 11 and 12 years.
Hence, their ages after 5 years will be 16 and 17 years.








Comments