The process of solving real-world problems can be simplified using the concepts of Algebra. In Algebra we use letters or symbols or alphabets to represent an unknown quantity and these quantities are known as “variables”. The real-world problem is then restated in the form of equations using variables and then systematic techniques of equation solving are followed step by step. Thus, to solve problems with the help of algebra the first step is to convert the problem into mathematical statements in such a way that it clearly illustrates the relationship between the unknowns and the information provided. Converting the real-life problem into a mathematical statement is usually the toughest step involved in solving the problem. Once a mathematical relationship has been established problem-solving becomes easy.
Applications of Linear Equations
Linear equations can be applied to solve real-world problems at a large scale. Let us begin with the practical application of linear equations in our day-to-day lives. Linear equations can find their way into every possible scenario. Suppose you went to the market to buy a few notebooks. There were two different sizes of notebooks available. The shopkeeper told you that the price of the thinner notebook is 4 times less than the price of the thicker notebook. Also, the total money that you brought from your home is Rs. 100. Can you figure out the cost of each type of notebook, if you could buy one notebook of each type with your Rs. 100 note.
Let us translate this problem into a mathematical statement. If the price of the thinner notebook is assumed to be ‘x’, then the price of the thicker notebook would be ‘4x’. Now according to the problem statement ‘x + 4x = 100’. This mathematical statement is a linear equation in one variable and can be solved using the rules of solving linear equations.
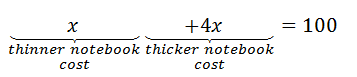
The value of ‘x’ comes out to be 20. It implies that the cost of the thinner notebook is 20 rupees and the cost of the thicker notebook is 4x i.e. 80 rupees.
The key to converting the problem into a mathematical statement is to carefully read the problem statement and identify the specific keywords, and phrases and use the minimum number of unknowns or variables.

Comments