Argument of Complex Numbers

The complex plane plays an important role in Mathematics. It is also known as z-plane, which is composed of two mutually perpendicular lines called axes. The horizontal line represents real numbers and is known as the real axis. On the other hand, the vertical line denotes imaginary numbers and is termed as an imaginary axis. The complex plane is used to represent a geometric interpretation of complex numbers. This plane is similar to the Cartesian plane having real and imaginary parts of a complex number along with X and Y axes. There are two concepts related to complex numbers. They are magnitude and argument. In this article, let us discuss in detail about the definition, properties, formulas for the argument of complex numbers.

What are Complex Numbers?

A complex number is a number that is written as a + ib, in which “a” is a real number, and “b” is an imaginary number. The complex number contains a symbol “i” which satisfies the condition i² = −1. Complex numbers can be referred to as the extension of the one-dimensional number line. In the complex plane, a complex number denoted by a + bi is represented in the form of the point (a, b). It is to be noted that a complex number with zero real part, such as – i, -5i, etc, is called purely imaginary. Also, a complex number with zero imaginary part is known as a real number.

Argument of Complex Numbers Definition

The argument of a complex number is defined as the angle inclined from the real axis in the direction of the complex number represented on the complex plane. It is denoted by “θ” or “φ”. It is measured in the standard unit called “radians”.

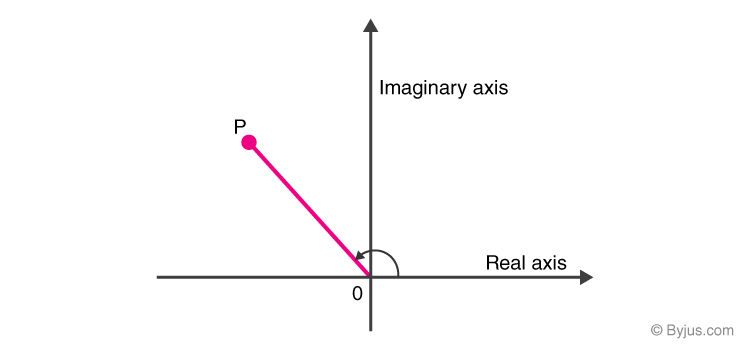
In this diagram, the complex number is denoted by the point P. The length OP is known as magnitude or the modulus of a number, while the angle at which OP is inclined from the positive real axis is said to be the argument of the point P.

Argument of Complex Numbers Formula

In polar form, a complex number is represented by the equation r(cos θ + i sin θ), here, θ is the argument. The argument function is denoted by arg(z), where z denotes the complex number, i.e. z = x + iy. The computation of the complex argument can be done by using the following formula:

arg (z) = arg (x+iy) = tan^-1(y/x)

Therefore, the argument θ is represented as:

θ = tan^-1 (y/x)

Properties of Argument of Complex Numbers

Let us discuss a few properties shared by the arguments of complex numbers. Suppose that z be a nonzero complex number and n be some integer, then

arg(zⁿ) = n arg(z)

Let us assume, z₁ and z₂ be the two complex numbers, the following identities are:

• arg (z₁/ z₂) = arg ( z₁) – arg ( z₂)
• arg ( z₁ z₂) = arg ( z₁) + arg ( z₂)

How to Find the Argument of Complex Numbers?

1. Find the real and imaginary parts from the given complex number. Denote them as x and y respectively.
2. Substitute the values in the formula θ = tan^-1 (y/x)
3. Find the value of θ if the formula gives any standard value, otherwise write it in the form of tan^-1 itself.
4. This value followed by the unit “radian” is the required value of complex argument for the given complex number.

Example

Question:

Find the argument of the complex number 2 + 2√3i.

Solution:

Let z = 2 + 2√3i.

Here, the real part, x = 2

Imaginary part, y = 2√3

We know that the formula to find the argument of a complex number is

arg (z) = tan^-1(y/x)

arg (z) = tan^-1(2√3/2)

arg (z) = tan^-1(√3)

arg (z) = tan^-1(tan π/3)

arg (z) = π/3

Therefore, the argument of the complex number is π/3 radian.

Register with BYJU’S – The Learning App and download the app to watch the interactive videos.