Boolean Algebra Laws

Class Registration Banner

Boolean algebra is a branch of mathematics that deals with the manipulation of variables which can assume only two truth values, true or false, denoted by 1 and 0, respectively. In this article, we shall discuss the Boolean algebra laws used to perform operations on Boolean variables.

Boolean algebra is named after English mathematician George Boole, who first introduced this concept in his book, “The Mathematical Analysis of Logic”. The idea of Boolean algebra became the basis of digital electronics and provided essential logic systems for modern computer programming languages. Unlike general variables, Boolean variables can either have the values 1 or 0, which denotes the state of ON and OFF in digital electronics. The primary operations which are performed over these variables are addition and multiplication. Let us learn the Boolean algebra laws and theorems to perform the arithmetic operations over Boolean variables.

Download PDF of Boolean Algebra Laws

Operations in Boolean Algebra

Before understanding the laws of Boolean algebra, let us quickly go through the various logic operations and their truth values used in Boolean algebra for calculation.

The basic logic operations are

Logic Operation Logic Operator Notation Truth Value
Boolean multiplication/Conjunction AND p . q or p Λ q The result is true when both statements are true.
Boolean addition/Disjunction OR p + q or p ν q  The result is true when both or either of the statements is true.
Boolean complement/Negation NOT ㄱp or ~p or p’ or pC The result is true when the statement is false and false when it is true.

Know more about truth value and logic operators.

What are Boolean Algebra Laws?

Boolean algebra laws and theorems are a set of rules that are required to reduce or simplify any given complex Boolean expression. Follwing is a list of Boolean algebra laws that are most commonly used.

Boolean laws Description 
Annulment law
  • A . 0 = 0
  • A + 1 = 1
Identity law
  • A . 1 = A 
  • A + 0 = A
Idempotent law
  • A . A = A 
  • A + A = A
Complement law
  • A . AC = 0
  • A + AC = 1
Commutative Law
  • A . B = B . A
  • A + B = B + A
Associative law
  • A . (B . C) = (A . B) . C 
  • A + (B + C) = (A + B) + C
Distributive law
  • A(B + C) = AB + AC
  • A + (BC) = (A + B)(A + C)
Absorption law
  • A.(A + B) = A
  • A + (A . B) = A
Involution law
  • (A’)’ = A
De Morgan’s law
  • (A + B)C = AC . BC
  • (A . B)C = AC + BC

In addition to these Boolean algebra laws, we have a few Boolean postulates which are used to algebraically solve Boolean expressions into a simplified form.

  • 0.0 = 0; Boolean multiplication of 0
  • 1.1 = 1; Boolean multiplication of 1
  • 0 + 0 = 0; Boolean addition of 0
  • 1 + 1 = 1; Boolean addition of 1
  • 1.0 = 0; Boolean multiplication of 1 and 0
  • 1 + 0 = 1; Boolean addition of 1 and 0
  • 1’ = 0; Boolean complement of 1
  • 0’ = 1; Boolean complement of 0

Application of Boolean Algebra Laws

As we have already stated laws of Boolean algebra have their application in digital electronics. Let us see how these laws are used in switching circuits.

Boolean Algebra Applications

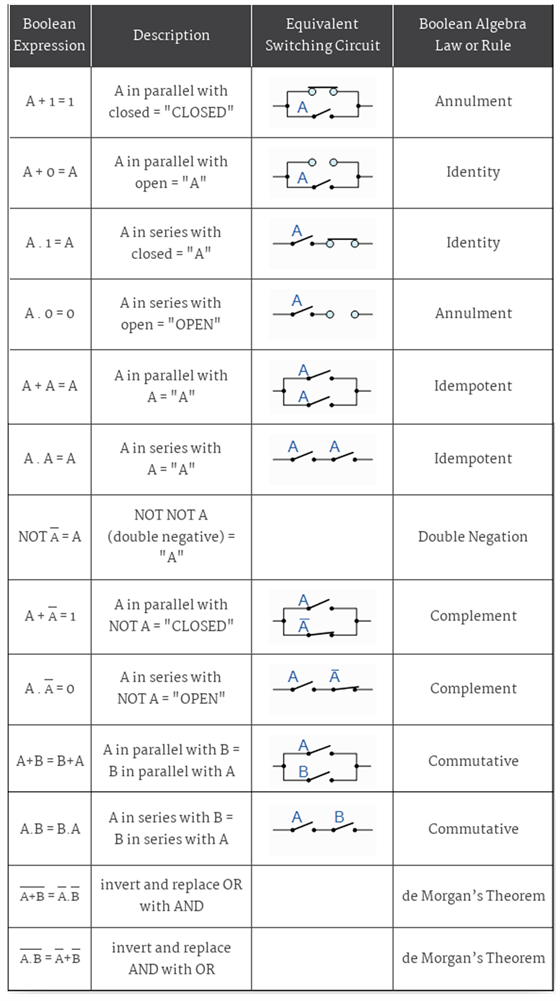
Related Articles

Solved Examples on Boolean Algebra Laws

Now, let us apply these Boolean laws to simplify complex Boolean expressions and find an equivalent reduced Boolean expression.

Example 1: 

Simplify the following Boolean expression: (A + B).(A + C).

Solution:

Let us simplify the given Boolean expression (A + B).(A + C) using relevant Boolean laws.

Proof Boolean Laws
(A + B).(A + C) = AA + AC + BA + BC Distributive law
= A + AC + AB + BC Idempotent AND law and commutative AND law
= A + AB + BC Absorption law (A + AC = A)
= A + BC Absorption law

Thus, (A + B).(A + C) = A + BC

Example 2: 

Simplify the following Boolean expression: (X + Y).(Xc + Y).

Solution:

Given Boolean expression, (X + Y).(Xc + Y)

Proof Boolean Laws
(X + Y).(Xc + Y) = XXc + XY + XcY + YY Distributive law
= 0 + XY + XcY + Y Complement and idempotent law
= XY + XcY + Y Identity law
= (X + Xc) Y + Y Distributive law
= 1.Y + Y Complement law
= Y + Y Identity law
= Y Idempotent law

Thus, the simplified Boolean expression is (X + Y).(Xc + Y) = Y.

Practice Problems on Boolean Algebra Laws

  1. Prove the absorption laws of Boolean algebra.
  2. Simplify the following Boolean expression: p’q’r + p’qr + pq’
  3. Simplify the following Boolean expression: AB + A’C +BC

Recommended Video

 

Watch other related videos on BYJU’S – The Learning App to learn about Boolean algebra calculator, Boolean algebra tutorials, and Boolean algebra simplification.

Frequently Asked Questions on Boolean Algebra Laws

Q1

What is De Morgan’s law in Boolean algebra?

According to De Morgan’s law for Boolean variables A and B, (A + B)’ = A’ . B’ and (A . B)’ = A’ + B’.

Q2

What is absorption law in Boolean algebra?

Following is the absorption law in Boolean algebra:
A + AB = A
A(A + B) = A

Q3

State the associative laws in Boolean algebra.

The associative laws in Boolean algebra are
A . (B . C) = (A . B) . C
A + (B + C) = (A + B) + C

Q4

What is the idempotent law in Boolean algebra?

The idempotent law in Boolean algebra states that
A . A = A
A + A = A

Q5

State the commutative law in Boolean algebra.

According to the commutative law:
A . B = B . A
A + B = B + A

MATHS Related Links
Important Questions Class 9 Maths Chapter 15 Probability Perimeter Of A Sector
Introduction To Data Level Of Significance
Important 6 Marks Questions For CBSE 11 Maths Three Dimensional Geometry
Negative Numbers: Connection To Daily Life Algebra Formulas For Class 11
What Is A Cyclic Quadrilateral Measures Of Central Tendency- Mean, Median And Mode

Comments

Leave a Comment

Your Mobile number and Email id will not be published.

*

*

  1.  Peter Packiam
    April 16, 2020 at 11:08 pm

    I was browsing through your impressive website,
    I enjoyed it thanks, Guys.

    Reply
  2. Saranya
    September 17, 2020 at 1:02 am

    It’s easy to understand. Thanks byjus team

    Reply